Gödel, Escher, Bach: An Eternal Golden Braid (119 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

4 is similar to 3.
A circle is a closed curve.
A closed curve has an interior and an exterior.
"Interior" and "exterior" are opposites.
The network of concepts is necessarily very vast. It seems to store knowledge only statically, or declaratively, but that is only half the story. Actually, its knowledge borders on being procedural as well, by the fact that the proximities in the net act as guides, or "programs", telling the main program how to develop its understanding of the drawings in the boxes.
For instance, some early hunch may turn out to be wrong and yet have the germ of the right answer in it. In BP 33 (Fig. 124), one might at first
FIGURE 124
. Bongard problem 33. [From M. Bongard, Pattern Recognition.]
jump to the idea that Class I boxes contain "pointy" shapes, Class II boxes contain
"smooth" ones. But on closer inspection, this is wrong. Nevertheless, there is a worthwhile insight here, and one can try to push it further, by sliding around in the network of concepts beginning at "pointy". It is close to the concept "acute", which is precisely the distinguishing feature of Class I. Thus one of the main functions of the concept network is to allow early wrong ideas to be modified slightly, to slip into variations which may be correct.
Slippage and Tentativity
Related to this notion of slipping between closely related terms is the notion of seeing a given object as a variation on another object. An excellent example has been mentioned already-that of the "circle with three indentations", where in fact there is no circle at all. One has to be able to bend concepts, when it is appropriate.
Nothing should be absolutely rigid. On
the other hand, things shouldn't be so wishy-washy that nothing has any meaning at all, either. The trick is to know when and how to slip one concept into another.
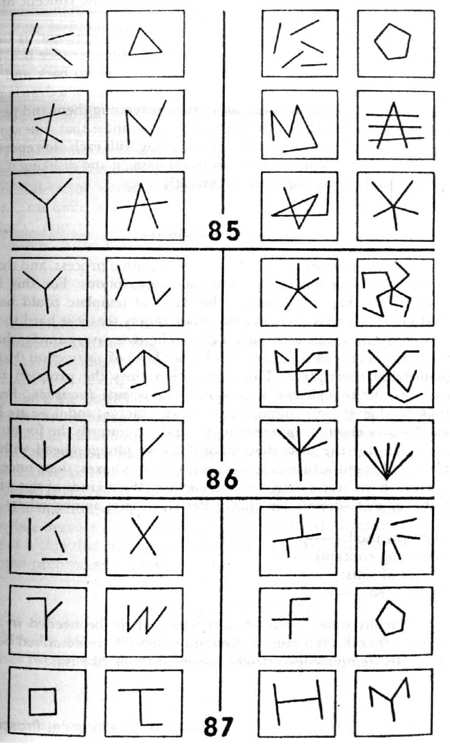
An extremely interesting set of examples where slipping from one description to another is the crux of the matter is given in Bongard problems 85-87 (Fig. 125).
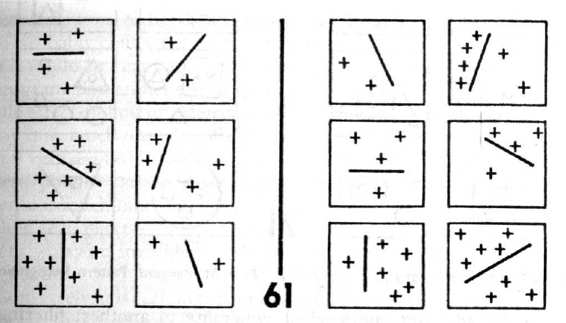
BP 85 is rather trivial. Let us assume that our program identifies "line segment" in its preprocessing stage. It is relatively simple for it then to count line segments and arrive at the difference
FIGURE 125.
Bongard problems 85-87. [From M. Bongard, Pattern Recognition
.]
between Class I and Class II in BP 85. Now it goes on to BP 86. A general heuristic which it uses is to try out recent ideas which have worked. Successful repetition of recent methods is very common in the real world, and Bongard does not try to outwit this kind of heuristic in his collection-in fact, he reinforces it, fortunately. So we plunge right into problem 86 with two ideas ("count" and "line segment") fused into one: "count line segments". But as it happens, the trick of BP
86 is to count line trains rather than line segments, where "line train" means an end-to-end concatenation of (one or more) line segments. One way the program might figure this out is if the concepts "line train" and "line segment" are both known, and are close in the concept network. Another way is if it can invent the concept of "line train"-a tricky proposition, to say the least.
Then comes BP 87, in which the notion of "line segment" is further played with. When is a line segment three line segments? (See box II-A.) The program must be sufficiently flexible that it can go back and forth between such different representations for a given part of a drawing. It is wise to store old representations, rather than forgetting them and perhaps having to reconstruct them, for there is no guarantee that a newer representation is better than an old one. Thus, along with each old representation should be stored some of the reasons for liking it and disliking it. (This begins to sound rather complex, doesn't it?)
Meta- Descriptions
Now we come to another vital part of the recognition process, and that has to do with levels of abstraction and meta-descriptions. For this let us consider BP 91
(Fig. 121) again. What kind of template could be constructed here? There is such an amount of variety that it is hard to know where to begin. But this is in itself a clue! The clue says, namely, that the class distinction very likely exists on a higher level of abstraction than that of geometrical description. This observation clues the program that it should construct
descriptions of descriptions
-that is,
meta
-
descriptions
. Perhaps on this second level some common feature will emerge; and if we are lucky, we will discover enough commonality to guide us towards the formulation of a template for the meta-descriptions! So we plunge ahead without a template, and manufacture descriptions for various boxes; then, once these descriptions have been made, we describe them. What kinds of slot will our template for meta-descriptions have? Perhaps these, among others: concepts used: ----
recurring concepts-----:
names of slots: -----
filters used:----
There are many other kinds of slots which might be needed in metadescriptions, but this is a sample. Now suppose we have described box I-E of BP 91. Its (template-less) description might look like this:
horizontal line segment
vertical line segment mounted on the horizontal line segment
vertical line segment mounted on the horizontal line segment
vertical line segment mounted on the horizontal line segment
Of course much information has been thrown out: the fact that the three vertical lines are of the same length, are spaced equidistantly, etc. But it is plausible that the above description would be made. So the meta description might look like this: concepts used:
vertical-horizontal, line segment, mounted on
repetitions in description:
3 copies of "vertical line segment mounted on the
horizontal line segment"
names of slots-----
filters used:-----
Not all slots of the meta-description need be filled in; information can be thrown away on this level as well as on the Just- plain-description" level.
‘Now if we were to make a description for any of the other boxes of Class I, and then a meta-description of it, we would wind up filling the slot "repetitions in description" each time with the phrase "3 copies of ..." The sameness-detector would notice this, and pick up three-ness as a salient feature, on quite a high level of abstraction, of the boxes of Class I. Similarly, four-ness would be recognized, via the method of metadescriptions, as the mark of Class II.
Flexibility Is Important
Now you might object that in this case, resorting to the method of metadescriptions is like shooting a fly with an elephant gun, for the three-ness versus four-ness might as easily have shown up on the lower level if we had constructed our descriptions slightly differently. Yes, true-but it is important to have the possibility of solving these problems by different routes. There should be a large amount of flexibility in the program; it should not be doomed if, malaphorically speaking, it "barks up the wrong alley" for a while. (The amusing term "malaphor" was coined by the newspaper columnist Lawrence Harrison; it means a cross between a malapropism and a metaphor. It is a good example of
"recombinant ideas".) In any case, I wanted to illustrate the general principle that says: When it is hard to build a template because the preprocessor finds too much diversity, that should serve as a clue that concepts on a higher level of abstraction are involved than the preprocessor knows about.
Focusing and Filtering
Now let us deal with another question: ways to throw information out. This involves two related notions, which I call "focusing" and "filtering".
Focus
-
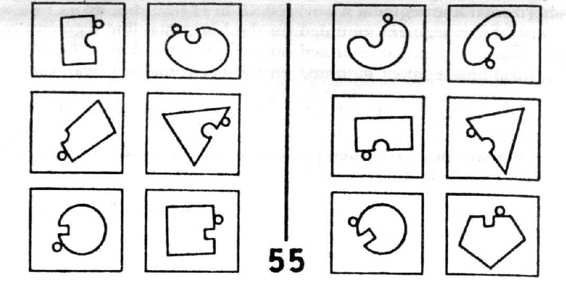
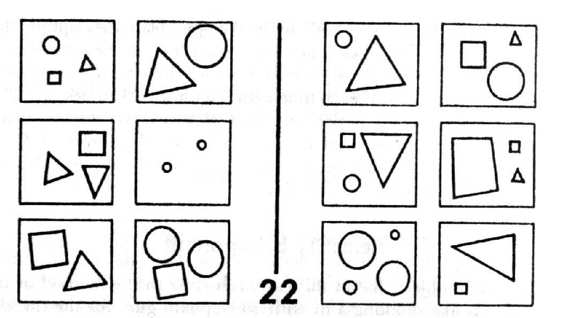
FIGURE 126.
Bongard problem 55. [From M. Bongard, Pattern Recognition
.]
FIGURE 127.
Bongard problem 22. [From M. Bongard, Pattern Recognition
.]
ing
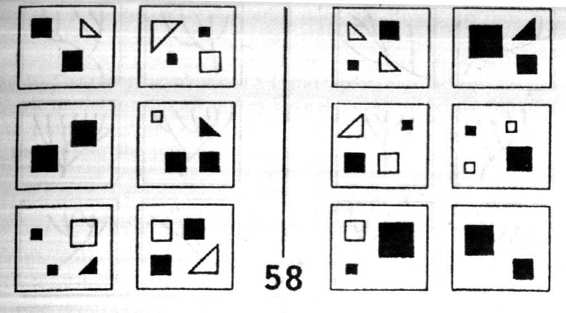
involves making a description whose focus is some part of the drawing in the box, to the exclusion of everything else. Filtering involves making a description which concentrates on some particular way of viewing the contents of the box, and deliberately ignores all other aspects. Thus they are complementary: focusing has to do with objects (roughly, nouns), and filtering has to do with concepts (roughly, adjectives). For an example of focusing, let's look at BP 55 (Fig. 126). Here, we focus on the indentation and the little circle next to it, to the exclusion of the everything else in the box. BP 22 (Fig. 127) presents an example of filtering. Here, we must filter out every concept but that of size. A combination of focusing and filtering is required to solve problem BP 58 (Fig. 128).
One of the most important ways to get ideas for focusing and filtering is by another sort of "focusing": namely, by inspection of a single particularly simple box-say one with as few objects in it as possible. It can be