A Field Guide to Lies: Critical Thinking in the Information Age (11 page)
Read A Field Guide to Lies: Critical Thinking in the Information Age Online
Authors: Daniel J. Levitin

But wait: Are the kinds of people who visit San Francisco representative of others? You’d skew toward people who can afford to travel there, and people who want to spend their vacation in a city, as opposed to, say, a national park. (You might also skew toward liberals, because San Francisco is a famously liberal city.)
So you decide that you can’t afford to study U.S. attitudes, but you can study attitudes about climate change among San Franciscans. You set up your helpers in Union Square and stop passersby with a short questionnaire. You instruct them to seek out people of different ages, ethnicities, styles of dress, with and without tattoos—in short, a cross-section with variability. But you’re still in trouble. You’re unlikely to encounter the bedridden, mothers with small
children, shift workers who sleep during the day, and the hundreds of thousands of San Francisco residents who, for various reasons, don’t come to Union Square, a part of town known for its expensive shops and restaurants. Sending half your helpers down to the Mission District helps solve the problem of different socioeconomic statuses being represented, but it doesn’t solve your other problems. The test of a random sample is this: Does everyone or -thing in the whole group have an equal chance of being measured by you and your team? Here the answer is clearly no.
So you conduct a
stratified
random sample. That is, you identify the different strata or subgroups of interest and draw people from them in proportion to the whole population. You do some research about climate change and discover that
attitudes do not seem to fall upon racial lines, so you don’t need to create subsamples based on race. That’s just as well because it can be difficult, or offensive, to make assumptions about race, and what do you do with people of mixed race? Put them in one category or another, or create a new category entirely? But then what? A category for Americans who identify as black-white, black-Hispanic, Asian-Persian, etc.? The categories then may become so specific as to create trouble for your analysis because you have too many distinct groups.
Another hurdle: You want age variability, but people don’t always feel comfortable telling you their age. You can choose people who are obviously under forty and obviously over forty, but then you miss people who are in their late thirties and early forties.
To even out the problem of people who aren’t out and about during the day, you decide to go to people’s homes door-to-door. But if you go during the day, you miss working people; if you go during the evening, you miss nightclubbers, shift workers, nighttime church-service attendees, moviegoers, and restaurant-goers. Once you’ve stratified, how do you get a random sample within your subgroups? All the same problems described above still persist—creating the subgroups doesn’t solve the problem that within the subgroup you still have to try to find a fair representation of all the
other
factors that might make a difference to your data. It starts to feel like we will have to sample all the rocks on the moon to get a good analysis.

Don’t throw in the trowel—er, towel. Stratified random sampling is better than non-stratified. If you take a poll of college students drawn at random to describe their college experience, you may end up with a sample of students only from large state colleges—a random sample is more likely to choose them because there are so many more of them. If the college experience is radically different
at small, private liberal-arts colleges, you need to ensure that your sample includes students from them, and so your stratified sample will ensure you ask people from different-sized schools. Random sampling should be distinguished from convenience or quota sampling—the practice of just talking to people whom you know or people on the street who look like they’ll be helpful. Without a random sample, your poll is very likely to be biased.
Collecting data through sampling therefore becomes a never-ending battle to avoid sources of bias. And the researcher is never entirely successful. Every time we read a result in the newspaper that 71 percent of the British are in favor of something, we should reflexively ask, “Yes, but
71 percent of
which
British?”
Add to this the fact that any questions we ask of people are only a sample of all the possible questions we could be asking them, and their answers may only be a sample of what their complex attitudes and experiences are. To make matters worse, they may or may not understand what we’re asking, and they may be distracted while they’re answering. And, more frequently than pollsters like to admit, people sometimes give an intentionally wrong answer. Humans are a social species; many try to avoid confrontation and want to please, and so give the answer they think the pollster wants to hear. On the other hand, there are disenfranchised members of society and nonconformists who will
answer falsely just to shock the pollster, or as a way to try on a rebellious persona to see if it feels good to shock and challenge.
Achieving an unbiased sample isn’t easy. When hearing a new statistic, ask, “What biases might have crept in during the sampling?”
Samples give us estimates of something, and they will almost always deviate from the true number by some amount, large or
small, and that is the margin of error. Think of this as
the price you pay for not hearing from everyone in the population under study, or sampling every moon rock. Of course, there can be errors even if you’ve interviewed or measured every single person in the population, due to flaws or biases in the measurement device. The margin of error does not address underlying flaws in the research, only the degree of error in the sampling procedure. But ignoring those deeper possible flaws for the moment, there is another measurement or statistic that accompanies any rigorously defined sample: the confidence interval.
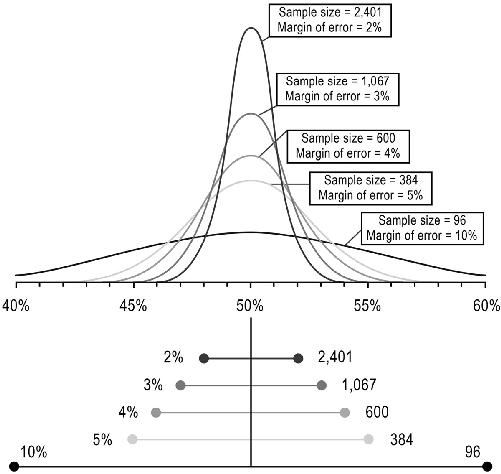
The margin of error is how accurate the results are, and the confidence interval is how confident you are that your estimate falls within the margin of error. For example, in a standard two-way poll (in which there are two possibilities for respondents), a random sample of 1,067 American adults will produce a margin of error around 3 percent in either direction (we write ±3%). So if a poll shows that 45 percent of Americans support Candidate A, and 47 percent support Candidate B, the true number is somewhere between 42 and 48 percent for A, and between 44 and 50 percent for B.
Note that these ranges overlap. What this means is that the two-percentage-point difference between Candidate A and Candidate B is within the margin of error: We can’t say that one of them is truly ahead of the other, and so the election is too close to call.
How confident are we that the margin of error is 3 percent and not more? We calculate a confidence interval. In the particular case I mentioned, I reported the 95 percent confidence interval. That means that if we were to conduct the poll a hundred times, using the same sampling methods, ninety-five out of those hundred times
the interval we obtain will contain the true value.
Five times out of a hundred, we’d obtain a value outside that range. The confidence interval doesn’t tell us how far out of the range—it could be a small difference or a large one; there are other statistics to help with that.
We can set the confidence level to any value we like, but 95 percent is typical. To achieve a narrower confidence interval you can do one of two things:
increase
the sample size for a given confidence level; or, for a given sample size,
decrease
the confidence level. For a given sample size, changing your confidence level from 95 to 99 will increase the size of the interval. In most instances the added expense or inconvenience isn’t worth it, given that a variety of external circumstances can change people’s minds the following day or week anyway.
Note that for very large populations—like that of the United States—we only need to sample a very small percentage, in this case, less than .0005 percent. But for smaller populations—like that of a corporation or school—we require a much larger percentage. For a company with 10,000 employees, we’d need to sample 964 (almost 10 percent) to obtain the 3 percent margin with 95 percent confidence, and for a company of 1,000 employees, we’d need to sample nearly 600 (60 percent).
Margin of error and confidence interval apply to sampling of any kind, not just samples with people: sampling the proportion of electric cars in a city, of malignant cells in the pancreas, or of mercury in fish at the supermarket. In the figure here, margin of error and sample size are shown for a confidence interval of 95 percent.
The
formula for calculating the margin of error (and confidence interval) is in the notes at the end of the book, and there are many online calculators to help. If you see a statistic quoted and no margin of error is given, you can calculate the margin yourself, knowing the number of people who were surveyed. You’ll find that in many cases, the reporter or polling organization doesn’t provide this information. This is like a graph without axes—you can lie with statistics very easily by failing to report the margin of error or confidence interval. Here’s one: My dog Shadow is the leading gubernatorial candidate in the state of Mississippi, with 76 percent of voters
favoring him over other candidates (with an unreported margin of error of ±76 percent; vote for Shadow!!!).
Sampling Biases
While trying to obtain a random sample, researchers sometimes make errors in judgment about whether every person or thing is equally likely to be sampled.
An infamous error was made in the 1936 U.S. presidential election. The
Literary Digest
conducted a poll and concluded that Republican Alf Landon would win over the incumbent Democrat, President Roosevelt. The
Digest
had polled people who were magazine readers, car owners, or telephone customers, not a random sample. The conventional explanation, cited in many scholarly and popular publications, is that in 1936, this skewed heavily toward the wealthy, who were more likely to vote Republican. In fact, according to a poll conducted by George Gallup in 1937,
this conventional explanation is wrong—car and telephone owners were more likely to back Roosevelt. The bias occurred in that Roosevelt backers were far less likely to participate in the poll. This sampling bias was recognized by Gallup, who conducted his own poll using a random sample, and correctly predicted the outcome. The Gallup poll was born. And it became the gold standard for political polling until it misidentified the winner in the 2012 U.S. presidential election.
An investigation uncovered serious flaws in their sampling procedures, ironically involving telephone owners.
Just as polls based on telephone directories skewed toward the wealthy in the 1930s and 1940s, now landline sampling skews
toward older people. All phone sampling assumes that people who own phones are representative of the population at large; they may or may not be. Many Silicon Valley workers use Internet applications for their conversations, and so phone sampling may underrepresent high-tech individuals.
If you want to lie with statistics and cover your tracks, take the average height of people near the basketball court; ask about income by sampling near the unemployment office; estimate statewide incidence of lung cancer by sampling only near a smelting plant. If you don’t disclose how you selected your sample, no one will know.
Participation Bias
Those who are willing to participate in a study and those who are not may differ along important dimensions such as political views, personalities, and incomes. Similarly, those who answer a recruitment notice—those who volunteer to be in your study—may show a bias toward or against the thing you’re interested in. If you’re trying to recruit the “average” person in your study, you may bias participation merely by telling them ahead of time what the study is about. A study about sexual attitudes will skew toward those more willing to disclose those attitudes and against the shy and prudish. A study about political attitudes will skew toward those who are willing to discuss them. For this reason, many questionnaires, surveys, and psychological studies don’t indicate ahead of time what the research question is, or they disguise the true purpose of the study with a set of irrelevant questions that the researcher isn’t interested in.
