Alan Turing: The Enigma (24 page)

Neglecting details as to margins, line control, and so forth, these ideas would suffice to give a complete description of the nature of a typewriter. An exact account of the configurations and positions allowed, and of how the character keys determined the symbols printed, the shift key the change of configuration from ‘lower’ to ‘upper’, and the space bar and backspace the printing position, would bring out the features most relevant to its function. If an engineer took this account, and created a physical machine which met its specifications, the result would be a typewriter, regardless of its colour, weight, or other attributes.

But a typewriter was too limited to serve as a model. It dealt with symbols, but it could only
write
them, and it required a human operator to choose the symbols and changes of configuration and position, one at a time. What, Alan Turing asked, would be the most
general
kind of machine that dealt with symbols? To be a ‘machine’ it would have to retain the typewriter’s quality of having a finite number of configurations, and an exactly determined behaviour in each. But it would have to be capable of much more. And so he imagined machines which were, in effect, super-typewriters.

To simplify the description he imagined his machines working with just one line of writing. This was only a technicality, which allowed margins and line control to be forgotten. But it was important that the supply of paper was to be assumed unlimited. In his picture, the typing point of his super-typewriter could progress indefinitely to left or right. For the sake of definiteness, he imagined the paper as being in the form of a
tape
, marked off into unit squares, such that just one symbol could be written on any one square. Thus his machines were to be finitely defined, but they would be allowed an unlimited amount of space on which to work.

Next, the machine would be able to
read
, or using his word, to ‘scan’ the square of tape on which it rested. It would still of course be able to write symbols, but now also to
erase
them. But it would only be able to move one place to the left or the right at a time. What role remained to the human operator of the typewriter? He did mention the possibility of what he called ‘choice machines’, in which an external operator would have the job of making decisions at certain points. But the thrust of his argument was
directed at what he called
automatic
machines, in which human intervention would play no part. For the goal of his development was the discussion of what Hardy had called ‘a miraculous machine’ – a mechanical process which could work on Hilbert’s decision problem, reading a mathematical assertion presented to it, and eventually writing a verdict as to whether it was provable or not. The whole point was that it should do so without the interference of human judgment, imagination or intelligence.

Any ‘automatic machine’ would work away by itself, reading and writing, moving to and fro, all in accordance with the way in which it was constructed. At every step its behaviour would be completely determined by the configuration it was in and the symbol it had read. To be precise, the construction of the machine would determine, for each combination of configuration and symbol scanned:

whether to write a new (specified) symbol in a blank square, to leave the existing one unchanged, or to erase it and leave a blank square

whether to remain in the same configuration, or to change to some other (specified) configuration

whether to move to the square on the left, or to the right, or to stay in the same position.

If all this information, defining an automatic machine, were written out, it would form a ‘table of behaviour’ of a finite size. It would completely define the machine in the sense that whether physically constructed or not, the table would hold all the relevant information about it. From this abstract point of view, the table
was
the machine.

Every different possible table would define a machine with a different kind of behaviour. There would be infinitely many possible tables, corresponding to infinitely many possible machines. Alan had rendered the vague idea of a ‘definite method’ or a ‘mechanical process’ into something very precise: a ‘table of behaviour’. And so now he had a very precise question to answer: was there or was there not one of these machines, one of these tables, that could produce the decision that Hilbert asked for?

An example machine: The following ‘table of behaviour’ completely defines a machine with the character of an adding machine. Started with the ‘scanner’ somewhere to the left of two groups of 1’s, separated by a single blank space, it will add the two groups, and stop. Thus, it will transform

into

The task of the machine is to fill in the blank space, and to erase the last ‘1’. It will therefore suffice to provide the machine with four configurations. In the first it moves along the blank tape looking for the first group of Ts. When it moves into the first group, it goes into the second configuration. The blank separator sends it into the third configuration, in which it moves along the second group until it encounters another blank,
which acts as the signal to turn back, and to enter the fourth and final configuration in which it erases the last ‘1’ and marks time for ever.

The complete table is:

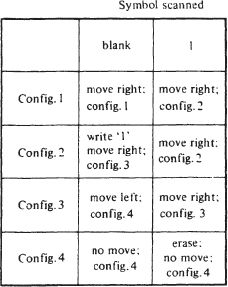
Even a very simple machine of this kind, as shown in the example, would be doing more than sums. The machine would effect acts of
recognition
, such as ‘finding the first symbol to the right’. A rather more complicated machine could perform multiplication, by repeated acts of copying out one group of 1’s, while erasing one at a time of another group of 1’s, and recognising when it had finished..Such a machine could also effect acts of
decision
, as for instance in deciding whether one number was divisible by another, or whether a given number was prime or composite. Clearly there was scope for exploiting this principle to mechanise a vast range of ‘definite methods’. But could there be such a machine that could decide Hilbert’s question about provability?

This was much too hard
a problem to approach by trying to write a ‘table’ to solve it. But there was an approach which led to the answer by a back door route. Alan hit on the idea of the ‘computable numbers’. The crucial notion was that any ‘real number’ which was defined by some definite rule could be calculated by one of his machines. For instance, there would be a machine to calculate the decimal expansion of π, rather as he had done at school. For it would require no more than a set of rules for adding, multiplying, copying, and so forth. being an infinite decimal, the work of the machine would never end, and it would need an unlimited amount of working space on its ‘tape’. But it would arrive at every decimal place in
some
finite time, having used only a finite quantity of tape. And everything about the process could be defined by a finite table, left alone to work on a blank tape.

This meant that he had a way of representing a number like π, an infinite decimal, by a
finite
table. The same would be true of the square root of three, or the logarithm of seven – or any other number defined by some rule. Such numbers he called the ‘computable numbers’.

More precisely, the machine itself would know nothing about decimals or decimal places. It would simply produce a sequence of digits. A sequence that could be produced by one of his machines, starting on a blank tape, he called a ‘computable sequence’. Then an infinite computable sequence, prefaced by a decimal point, would define a ‘computable number’ between 0 and 1. It was in this more strict sense that any computable number between 0 and 1 could be defined by a finite table. It was important to his argument that the computable numbers would always be expressed as infinite sequences of digits, even if these were all 0 after a certain point.

But these finite tables could now be put into something like alphabetical order, beginning at the most simple, and working through larger and larger ones. They could be put in a list, or counted; and this meant that all the computable numbers could be put in a list. It was not a practical proposition actually to do it, but in principle the idea was perfectly definite, and would result in the square root of three being say 678th in order, or the logarithm of
π
being 9369th. It was a staggering thought, since this list would include every number that could be arrived at through arithmetical operations, finding roots of equations, and using mathematical functions like sines and logarithms – every number that could possibly arise in computational mathematics. And once he had seen this, he knew the answer to Hilbert’s question. Probably it was this that he suddenly saw on the Grantchester meadow. He would have seen the answer because there was a beautiful mathematical device, ready to be taken off the shelf.

Fifty years earlier, Cantor had realised that he could put all the fractions – all the ratios or
rational
numbers – into a list. Naively it might be thought that there were many more fractions than integers. But Cantor showed that, in a precise sense, this was not so, for they could be counted off, and put
into a sort of alphabetical order. Omitting fractions with cancelling factors, this list of all the rational numbers between 0 and 1 would begin:

1/2 1/3 1/4 2/3 1/5 1/6 2/5 3/4 1/7 3/5 1/8 2/7 4/5 1/9 3/7 1/10…

Cantor went on to invent a certain trick, called the Cantor diagonal argument, which could be used as a proof that there existed
irrational
numbers. For this, the rational numbers would be expressed as infinite decimals, and the list of all such numbers between 0 and 1 would then begin:

1. 5
   000000000000000000.…
   
2. 3
   3
   33333333333333333.…
   
3. 25
   0
   0000000000000000.…
   
4. 666
   6
   666666666666666.…
   
5. 2000
   0
   00000000000000.…
   
6. 16666
   6
   6666666666666.…
   
7. 400000
   0
   000000000000.…
   
8. 7500000
   0
   00000000000.…
   
9. 14285714
   2
   8571428571.…
   
10. 600000000
    0
    000000000.…
    
11. 1250000000
    0
    00000000.…
    
12. 28571428571
    4
    2857142.…
    
13. 800000000000
    0
    000000.…
    
14. 1111111111111
    1
    11111.…
    
15. 42857142857142
    8
    5714.…
    
16. 100000000000000
    0
    000.…
    . .....
    . .....
    

The trick was to consider the diagonal number, beginning

.5306060020040180.…

and then to change each digit, as for instance by increasing each by 1 except by changing a 9 to a 0. This would give an infinite decimal beginning

.6417171131151291.…

a number which could not possibly be rational, since it would differ from the first listed rational number in the first decimal place, from the 694th rational number in the 694th decimal place, and so forth. Therefore it could not be in the list; but the list held all the rational numbers, so the diagonal number could not be rational.