Alan Turing: The Enigma (32 page)

This was the central problem of the theory of numbers, but there was a constellation of related questions, one of which Alan picked for his own investigation. The simple assumption that the primes thinned out like the logarithm, without Riemann’s refinements to the formula, seemed always to overestimate the actual number of primes by a certain amount. Common sense, or ‘scientific induction’, based on millions of examples, would suggest that this would always be so, for larger and larger numbers. But in 1914 Hardy’s collaborator J.E. Littlewood had shown that this was not so, for there existed some point where the simple assumption would underestimate the cumulative total of primes. Then in 1933 a Cambridge mathematician, S. Skewes, had shown
¹⁹
that if the Riemann Hypothesis were true, a crossover point would occur before

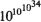
which, Hardy commented, was probably the largest number ever to serve any definite purpose in mathematics.
^*
It could be asked whether this enormous bound might be reduced, or whether one could be found that did not depend upon the truth of the Riemann Hypothesis, and these were the problems that Alan now undertook.

One
new departure at Cambridge was his acquaintance with Ludwig Wittgenstein, the philosopher. He would have seen Wittgenstein before at the Moral Science Club, and Wittgenstein (like Bertrand Russell) had received a copy of
Computable Numbers
. But it was in this summer of 1937 that Alister Watson, the King’s Fellow, introduced them and they met sometimes in the botanical gardens. Watson had written a paper
²⁰
on the foundations of mathematics for the Moral Science Club, in which he made use of the Turing machine. Wittgenstein, whose first work had been as an engineer, always liked practical, down-to-earth constructions and would have approved of the way that Alan had made a vague idea so definite. Curiously, the failure of the Hilbert programme had also meant the end of the point of view advanced by Wittgenstein in his first phase, in the
Tractatus Logico-Philosophicus
, that every well-posed problem could be solved.

Alan probably had a boating holiday – either on the Norfolk Broads, or at Bosham on Chichester Harbour. He also stayed for a while with the Beuttells in London. Although Mr Beuttell in principle espoused liberal causes of feminism and profit-sharing, his own firm was run on strictly autocratic lines, and so was his family. Victor’s younger brother Gerard was studying physics at Imperial College, but his father was extremely annoyed that he spent his time flying model aeroplanes to investigate wind currents, and put a stop to his studies. Alan was furious to hear this, saying that Gerard had a contribution to make to science,
²¹
and was doubly upset because he respected his father. He also roared with approval when he heard that Gerard had told his father, in connection with his infringing some petty rule of the family firm, that he would only obey ‘sensible rules’.

It was also in London that Alan met James again for a weekend. They stayed at a rather sordid bed-and-breakfast place near Russell Square. They went to see a film or two and Elmer Rice’s play
Judgment Day
about the Reichstag fire trial. Alan must have found it a relief to be with someone who did not reject his sexual advances, although it was always clear that James aroused in him neither deep feelings, nor a special physical attraction. The relationship was not able to develop beyond this point. After this weekend, James had almost no further experience for about twelve years. Although Alan was more exploratory, this would be his story too. His life would not change until much water had flowed under the bridge.

On 22 September, Alan met up at Southampton with an American friend from Graduate College, Will Jones. They had arranged to travel back together, and boarded the German liner, the
Europa
. Will Jones had spent the summer at Oxford, and it was he who chose the German ship, simply because it was faster. A more dutiful anti-fascist than Alan would not have used it, but on the other hand a more conventional person would not have spent the voyage in learning Russian, enjoying the shocked German expressions as he wielded a textbook emblazoned with hammer and sickle.

On the boat, wrote Alan on arrival, he

Was very glad to have Will Jones as travelling companion. There didn’t seem to be anyone very interesting on board so Will and I whiled away the time with philosophical discussions, and spent half of one afternoon in trying to find the speed of the boat.

Back
at Princeton, Alan and Will Jones spent much time talking together. Will Jones came from the old white South of deepest Mississippi, and had studied philosophy at Oxford. So this was not the stereotyped meeting of Yankee brashness and old world elegance, far from it. Will Jones came from quite another America, just as Alan represented a plain-speaking, pragmatic, liberal England. As a philosopher with a serious interest in science, Will Jones also rose above the usual boundaries of arts and sciences. He was currently writing a dissertation on the claim of Kant that moral categories could be justified even if human actions were as determined as the motions of the planets. He canvassed Alan’s opinion as to whether quantum mechanics had affected the argument – so much the problem to which Alan had addressed himself five or so years before! But now he gave the impression that he had long been happy with the Russellian view, that at some level the world must evolve in a mechanistic way. He was not now very interested in philosophical, as opposed to scientific, discussions of the problem of free will. Perhaps the trace of his former conflict lay in his very vehemence in the materialist direction. ‘I think of people as
pink
-coloured collections of
sense-data
,’ he once joked. If only it were so easy! Symbolically, the Research fountain pen that Mrs Morcom had given him in 1932 was lost on the voyage.

Will Jones also had Alan explain to him some of the theory of numbers, and enjoyed the way that Alan did it, showing how from the most simple axioms, all the properties could be precisely derived – an approach quite different from the rote-learning of school mathematics. Alan never talked to Will about his emotional problems, but it might well be that he derived moral support in a much more general way, for Will appreciated in him the embodiment of the moral philosophy of G.E. Moore and Keynes.

Alan and Will had become aquainted through being members of the same circle of friends the previous year, and another of the circle had also returned to Princeton. This was Malcolm MacPhail, a Canadian physicist, who became involved in a sideline that Alan took up.
²²

It
was probably in the fall of 1937 that Turing first became alarmed about a possible war with Germany. He was at that time supposedly working hard on his famous thesis but nevertheless found time to take up the subject of cryptanalysis with characteristic vigour. … on this topic we had
many
discussions. He assumed that words would be replaced by numbers taken from an official code book and messages would be transmitted as numbers in the binary scale. But, to prevent the enemy from deciphering captured messages even if they had the code book, he would multiply the number corresponding to a specific message by a horrendously long but secret number and transmit the product. The length of the secret number was to be determined by the requirement that it should take 100 Germans working eight hours a day on desk calculators 100 years to discover the secret factor by routine search!

Turing actually designed an electric multiplier and built the first three or four stages to see if it could be made to work. For the purpose he needed relay-operated switches which, not being commercially available at that time, he built himself. The Physics Department at Princeton had a small but well equipped machine shop for its graduate students to use, and my small contribution to the project was to lend Turing my key to the shop, which was probably against all the regulations, and show him how to use the lathe, drill, press etc. without chopping off his fingers. And so, he machined and wound the relays; and to our surprise and delight the calculator worked.

Mathematically, this project was not advanced, for it used only multiplication. But although it used no advanced theory, it involved applications of ‘dull and elementary’ mathematics which were by no means well known in 1937.

For one thing, the binary representation of numbers would have seemed a novelty to anyone then engaged in practical computations. Alan had used binary numbers in
Computable Numbers
. There they brought in no point of principle, but made it possible to represent all the computable numbers as infinite sequences of 0s and 1s alone. In a practical multiplier, however, the advantage of binary numbers was more concrete: it was that the multiplication table then reduced to:

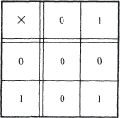
The binary multiplication table being so trivial, the work of a multiplier would be reduced to carrying and adding operations.

A second aspect of his project was its connection with elementary logic. The arithmetical operations with 0s and 1s could be thought of in terms of the logic of propositions. Thus the trivial multiplication table, for instance, could be considered as equivalent to the function of the word AND in logic. For if
p
and
q
were propositions, then the following ‘truth-table’ would show in what circumstances ‘p AND
q’
was true:

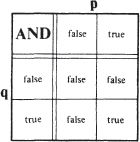
It
was the same game, with a different interpretation. All of this would have been entirely familiar to Alan, the calculus of propositions appearing on the first page of any text on logic. It was sometimes called ‘Boolean Algebra’ after George Boole, who had formalised what he optimistically called ‘the laws of thought’ in 1854. Binary arithmetic could all be expressed in terms of Boolean algebra, using AND, OR, and NOT. His problem in designing the multiplier would be to use Boolean algebra to minimise the number of these elementary operations required.

This, as a paper exercise, would be very similar to that of designing a ‘Turing machine’ for the same problem. But in order to embody it in working machinery, it required some means of arranging for different physical ‘configurations’. This was achieved by the switches, for the whole point of a switch would be that it could be in one of two states, ‘on’ or ‘off’, ‘0’ or ‘1’, ‘true’ or ‘false’. The switches that he used were operated by relays, and in this way electricity played its first direct part in his urge to connect logical ideas with something that physically worked. There was nothing new about the electromagnetic relay, which had been invented by the American physicist Henry a hundred years earlier. Its physical principle was the same as that of the electric motor, an electric current, passing through a coil, causing a magnetic head to move. However, the point of a relay was that the magnetic head would either open or close another electrical circuit. It would act as a switch. The name ‘relay’ derived from its use in early telegraph systems, to allow an enfeebled electric signal to set off a fresh, clean click. It was this all-or-nothing
logical
function of relays that made them necessary by the million in the automatic telephone exchanges proliferating in the United States and Britain alike.