Alex’s Adventures in Numberland (75 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Again, Cantor has led us to a very counter-intuitive world. Fractions, though they are infinite in number, are responsible for only a tiny, tiny part of the number line. They are much more lightly sprinkled along the line than the other type of number that makes up the number line, the numbers that cannot be expressed as fractions, which are our old friends the
irrational
numbers. It turns out that the irrational numbers are so densely packed that there are more of them in any finite interval on the number line than there are fractions on all of the number line.
We introduced
c
above as being the number of points on a number line between 0 and 1. How many points are there between 0 and 2, or between 0 and 100? Exactly
c
of them. In fact, between any two points on the number line there are exactly
c
points in between, no matter how far or close they are apart. What’s even more amazing is that the totality of points on the entire number line is also
c
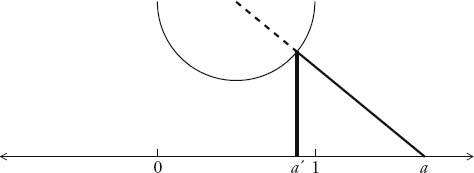
, and this is shown by the following proof, illustrated opposite. The idea is to show that there is a one-to-one correspondence between the points that lie between 0 and 1, and the points that lie on the entirety of the number line. This is done by pairing off every point on the number line with a point between 0 and 1. First, draw a semicircle suspended above 0 and 1. This semicircle acts like a matchmaker in that it fixes the couplings of the points between 0 and 1 and the points on the number line. Take any point on the number line, marked
a
, and draw a straight line from
a
to the centre of the circle. The line hits the semicircle at a point that is a unique distance between 0 and 1, marked
a'
, by drawing a line vertically down until it meets the number line. We can pair up every point marked
a
to a unique point
a'
in this way. As our chosen point
a
heads to plus infinity, the corresponding point between 0 and 1 closes in on 1, and as the chosen point heads to minus infinity, the corresponding point closes in on 0. If every point on the number line can be paired off with a unique point between 0 and 1, and vice versa, then the number of points on the number line must be equal to the number of points between 0 and 1.
The difference between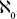 and
and
c
is the difference between the number of points on the number line that are fractions and the total number of points, including fractions and irrationals. The leap between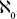 and
and
c
, however, is so immense that were we to pick a point at random from the number line, we have 0 percent probability of getting a fraction. There just aren’t enough of them, compared to the uncountably infinite number of irrationals.
Difficult as Cantor’s ideas were to accept at first, his invention of the aleph has been vindicated by history; not only is it now almost universally accepted into the numerical fold, but the zigzag and diagonal proofs are generally hailed as among the most dazzling in the whole of mathematics. David Hilbert said: ‘From the paradise created for us by Cantor, no one will drive us out.’
Unfortunately for Cantor, this paradise came at the expense of his mental health. After he recovered from his first breakdown, he began to focus on other subjects, such as theology and Elizabethan history, becoming convinced that the scientist Francis Bacon wrote the plays of William Shakespeare. Proving Bacon’s authorship became a personal crusade, and a focus for increasingly erratic behaviour. In 1911, giving a lecture at St Andrews University, where he had been invited to talk about mathematics, he instead discussed his views on Shakespeare, much to the embarrassment of his hosts. Cantor had several more breakdowns and was frequently hospitalized until his death in 1918.
A devout Lutheran, Cantor wrote many letters to clergymen about the significance of his results. He believed that his approach to infinity showed that it could be contemplated by the human mind, and therefore bring one closer to God. Cantor had Jewish ancestry, which – it has been argued – may have influenced his choice of the aleph as the symbol for infinity, since he may have been aware that in the mystical Jewish tradition of Kabbalah, the aleph represents the oneness of God. Cantor said he was proud he chose the aleph since, as the first letter of the Hebrew alphabet, it was a perfect symbol for a new beginning.
The aleph is also a perfect place for an end to our journey. Mathematics, as I wrote in the opening chapters of this book, emerged as part of man’s desire to make sense of his own environment. By making notches on wood, or counting with fingers, our ancestors invented numbers. This was helpful for farming and trade, and ushered us into ‘civilization’. Then, as mathematics developed, the subject became less about real things and more about abstract ones. The Greeks introduced concepts such as a point and a line, and the Indians invented zero, which opened the door to even more radical abstractions like negative numbers. While these concepts were at first counter-intuitive, they were assimilated quickly and we now use them on a daily basis. By the end of the nineteenth century, however, the umbilical cord linking mathematics to our own experience snapped once and for all. After Riemann and Cantor, maths lost its connection to any intuitive appreciation of the world.
After finding
c
Cantor kept going, proving that there are even bigger infinities. As we saw,
c
is the number of points on a line. It is also equal to the number of points on a two-dimensional surface. (That’s another surprising result, which you’ll have to trust me on.) Let’s call
d
the number of all possible curves, lines and squiggles that can be drawn on a two-dimensional surface. Using set theory, we can prove that
d
is bigger than
c
. And we can go one step further, showing that there must be an infinity larger than
d
. Yet no one has so far been able to come up with a set of things that has a cardinality larger than
d
.
Cantor led us beyond the imaginable. It is a rather wonderful place and one that is amusingly opposite to the situation of the Amazonian tribe I mentioned at the beginning of this book. The Munduruku have many things, but not enough numbers to count them. Cantor has provided us with as many numbers as we like, but there are no longer enough things to count.

Algorithm:
a set of rules or instructions designed to solve a problem.
Ambigram:
a word (or set of words) written in such a way as to conceal other words, often the same word (or set of words) written upside-down.
Amicable number:
two numbers are amicable if the factors of one add up to the other and vice versa.
Axiom:
a statement that is accepted without proof, usually because it is self-evident, and used as a foundation of a logical system.
Base:
in a number system, the base is the size of the number-grouping which, when using Arabic numerals, is equal to the number of different digits allowed in the system. Binary, using 0 and 1, is base two, while decimal, using 0 to 9, is base ten.
Cardinality:
the size of a set.
Circumference:
the perimeter of a circle.
Combinatorics:
the study of combinations and permutations.
Constant:
a fixed value.
Continuum:
the points on a continuous line.
Convergent series:
an infinite series that adds up to a finite number.
Correlation:
a measure of the interdependence of two variables.
Countable infinity:
an infinite set, the members of which can be put in a one-to-one correspondence with the natural numbers.
Cubic equation:
an equation of the form
ax
3
+
bx
2
+
cx
+
d
= 0, where
a
,
b
,
c
and
d
are constants and
a
is non-zero.
Curvature:
a property of space that can be determined by the behaviour of triangles or parallel lines.
Decimal fraction:
a fraction when written with a decimal point, so 1.5 is the decimal fraction equal to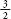 .
.
Denominator:
the number beneath the line in a fraction.
Diameter:
the width of a circle.
Distribution:
a spread of possible outcomes and their likelihood of occurring.
Divergent series:
an infinite series that does not add up to a finite number.
Divisor:
a natural number that divides into another number with no remainder; so 5 is a divisor of 20.
Dyscalculia:
a condition affecting one’s ability to grasp numbers.
Edge:
the chance of winning a gamble minus the chance of losing.
Egyptian triangle:
a triangle whose sides have the ratios 3:4:5.
Expected value:
the theoretical value of how much you can expect to win or lose in a bet.
Exponent:
the power of a number, written as a raised symbol, such as the
x
in 3
x
.
Factor:
a divisor of a given number.
Factorize:
to break a number down into its factors, usually just the ones that are prime numbers.
Fibonacci number:
a number in the Fibonacci series, which begins 1, 1, 2, 3, 5, 8, 13…
Gambler’s fallacy:
the false idea that random outcomes are not random.
Gambler’s ruin:
the inevitability of bankruptcy if you gamble for long enough.
Gaussian distribution:
the normal distribution.
Geometric progression:
a sequence of numbers in which each new term is calculated by multiplying the previous term by a fixed number.
Hyperbolic plane:
an infinitely large surface with negative curvature.
Hypotenuse:
the side of a right-angled triangle opposite the right angle.
Infinite series:
a series with an infinite number of terms.
Integer:
a number that is one of the natural numbers, negative natural numbers or zero.
Inversion:
the same thing as an ambigram.
Irrational number:
a number that cannot be expressed as a fraction.
Latin square:
a square grid where every element occurs only once in each row and column.
Law of large numbers:
the rule that probability works out in the long run, in that the more examples of a random event you have (such as the flipping of a coin), the closer the actual results will be to the expected results.
Law of very large numbers:
the rule that if the sample is large enough, then any result may occur no matter how unlikely.
Logarithm:
if
a
= 10
b
, then the logarithm of
a
is
b
, written log
a
=
b
.
Magic square:
a square grid containing consecutive numbers from 1 such that the sum of all rows, columns and diagonals are equal.
Mersenne prime:
a prime number that can be expressed as 2
n
– 1.
Natural number:
any whole number that can be reached counting upwards from 1.
Normal distribution:
the most common type of distribution, which produces the bell curve.
Normal number:
a number whose decimal digits consist of an equal number of 0s, 1s, 2s, 3s, 4s, 5s, 6s, 7s, 8s and 9s.
Number line:
a visual representation of numbers as points on a continuous line.
Numerator:
the number above the line in a fraction.
Order of magnitude:
Most commonly, the scale of a number based on the positional value of the leftmost digit of that number. So, the order of magnitude of any number between 1 and 9 is one, between 10 and 99 is two, between 100 and 999 is three, and so on.
Parallel:
two straight lines that never meet are parallel.
Perfect number:
a number that is equal to the sum of its divisors (excluding itself).
Phi:
the mathematical constant, the decimal expansion of which begins 1.618…, and is also known as the golden ratio, or the divine proportion.
Pi:
the mathematical constant, the decimal expansion of which begins 3.14159265358979323846…, and that is equal to the ratio between the circumference and the diameter of a circle.
Platonic solid:
the five solids whose sides are all identical regular polygons; in other words, the tetrahedron, cube, octahedron, icosahedron and dodecahedron.
Polygon:
a two-dimensional closed shape made up of a finite number of straight lines.
Postulate:
a statement that is assumed to be true, and used as an axiom.
Power:
an operation that determines how many times a number is to be multiplied by itself, so if 10 is to be multiplied by itself four times, one writes 10
4
and calls this ‘ten to the power of four’. Powers are not always natural numbers, but when one talks about the ‘powers of
x
’ it is assumed that one is referring only to the powers of
x
that are.
Prime number:
a natural number that has only two divisors, itself and 1.
Probability:
the chance of an event taking place, expressed as a fraction between 0 and 1.
Quadratic equation:
an equation of the form
ax
2
+
bx
+
c
= 0, where
a
,
b
, and
c
are constants and
a
is non-zero.
Radius:
a straight line from the centre of a circle to the circumference.
Randowalk:
a visual interpretation of randomness, in which each random event is expressed as movement in a random direction.
Rational number:
a number that can be expressed as a fraction.
Regression to the mean:
the phenomenon that after extreme events less extreme ones are more likely.
Regular polygon:
a polygon with sides of equal length and with equal internal angles.
Sequence:
a list of numbers.
Series:
the sum of the terms in a sequence.
Set:
a collection of things.
Tessellation:
an arrangement of tiles that fills a two-dimensional space completely with no overlaps.
Theorem:
a statement that can be proved from other theorems and/or axioms.
Transcendental number:
a number that cannot be expressed as a solution to a finite equation.
Uncountable infinity:
an infinite set whose members cannot be put in a one-to-one correspondence with the natural numbers.
Unique solution:
the situation when there is one and only one possible answer.
Variable:
a quantity that can vary in value.
Vertex:
where two lines meet to form an angle, or the angular points in a three-dimensional shape.
