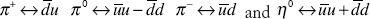Beyond the God Particle (42 page)
Read Beyond the God Particle Online
Authors: Leon M. Lederman,Christopher T. Hill
Tags: #Science, #Cosmology, #History, #Physics, #Nuclear, #General

The first three are the pions, and the fourth is called the “eta meson.” All four are known well from experiment, and their quark composition accounts neatly for the pattern. In fact, from the masses of the pions and other mesons, we can deduce the masses of quarks themselves.
Only particular combinations of quark composites are observed experimentally to occur. In nature we only find objects containing three quarks (called
baryons
), or three antiquarks (called
anti-baryons
), or objects containing quark plus antiquark (called
mesons)
. So the question arises: What is the nature of the strong force that holds the quarks together inside of the hadrons?
We find that each quark comes in “triplets.” That is, there are three up quarks, three down quarks, three strange quarks, and so on. The additional label is the “color.” Hence we say that there is a red up, a blue up, and a yellow up quark. This has nothing to do with visual colors of the rainbow but is a mnemonic description of the full symmetry of quarks.
The color of a quark is hard to detect, because any observed particle that the quarks compose, a hadron such as the proton and neutron and mesons,
always has a net color of zero
. For example, at any instant of time, the proton contains
uud
, but one quark is red, another blue, and another yellow, making an overall color-neutral state.
The antiquarks must be viewed as having anti-colors in the sense of the color wheel. So the anti–blue up quark is actually a red-yellow, or “cyan,” object. Therefore, we can make color-balanced mesons by combining pairs of quark and antiquark. This simple rule explains the forms of the bound particles that we see. However, it also gives the clue to the fundamental theory of the strong interactions.
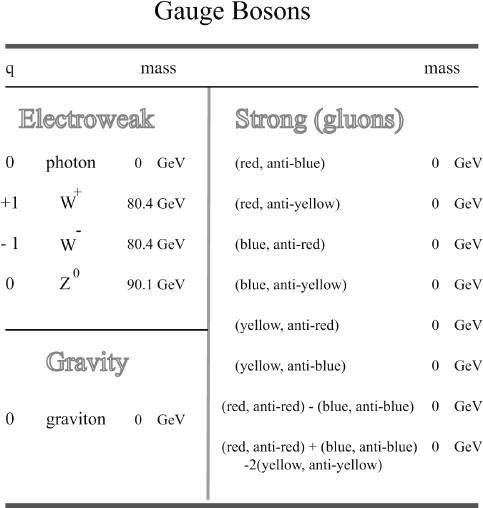
Figure A.36. Table of Gauge Bosons.
These are also the known “force carriers” and all are defined by “gauge” symmetries.
How do we establish that quark color exists if we can't see it? In fact, it was anticipated in the early days of the quark theory because of Pauli's exclusion principle. There exists a composite strongly interacting particle, whose properties Gell-Mann dramatically and precisely predicted in 1963. Experimentalists quickly confirmed the prediction at Brookhaven National Laboratory. This is the
Ω
–
, “omega-minus,” and it contains three strange quarks, or
sss
. It is known that the quarks making up the
Ω
–
must move in a single common quantum state, or orbital, but without quark color this would be
strictly forbidden
by the Pauli exclusion principle. Yet the
Ω
–
does indeed exist. The only way out of this conundrum is the existence of quark
color. If one s quark is red, the second blue, and the third yellow, making up the
Ω
–
, then there is no problem with the exclusion principle. There are many other ways in which the number of colors of quarks has been “counted” in experiment, and the result is always consistent with three.
We can think of a quark as though it lives in a “three-dimensional color space,” whose three axes are labeled by the three colors. In this space, a quark can be thought of as an arrow (a vector) that can point in any color direction. If the quark is red, its arrow points along the red axis, if blue, then the blue axis, and so forth. However, in quantum theory the arrow can rotate and point in any direction. The color symmetry is just the collection of rotations that we can do to such a quark arrow (this is known as the “symmetry group SU(3)”).
Now we generalize the subtle idea of “gauge symmetry,” which governs electrodynamics. For the electron, the symmetry requires the introduction of the photon. The electron becomes a quantum blend with the photon. Gauge symmetry then implies that by “shaking” (accelerating) the electron, we can cause the emission of a gauge particle, or
gauge boson
, called the photon. This gives rise to all of the electromagnetic properties of matter.
But for quarks, we go further with this concept. We can rotate the quarks in color space, for example, we can rotate a pure red down quark into a blue down quark. We want this to be a “gauge symmetry,” and this requires that we have additional particles that “undo” the changes we make on the red quark, keeping the overall result invariant. To have a color-gauge symmetry, we need 8 new gauge particles, called
gluons
.
5
The physical gluons are emitted from the quarks when the quarks accelerate, like photons from electrons. But gluons carry off the old color of the quark and carry in a new color. So a gluon has (color + anti-color). So, when we turn a red quark into a blue quark, by emitting a gluon we simultaneously
create a (red, anti-blue) gluon
, so the net color is (red + anti-blue) + (blue) = (red), and therefore initial color of the quark is recovered.
Note that if a gluon collides with a quark, the gluon will be absorbed and the quark will be accelerated. It is, perhaps, one of the most astounding aspects of modern science that the simple idea of a symmetry yields up the photon, and quantum electrodynamics likewise yields the correct theory of the strong interactions when it is adapted to quark color. This theory is called quantum chromodynamics (QCD), and it is a stunning success.
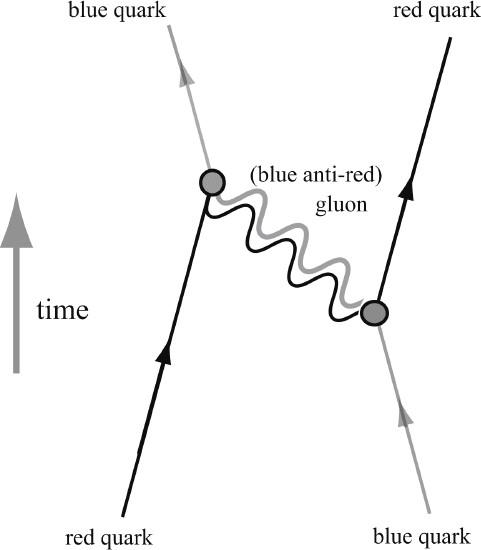
Quarks thus interact with one another by the exchange of gluons. We can draw the appropriate Feynman diagrams and learn how to compute them. The force is strong because the “color charge,” g, the analog of the electric charge, is large.
Figure A.37. Quark Exchanging Gluons.
A red quark scatters off of a blue quark. The quarks exchange color through the (red, anti-blue) gluon that hops between them, giving rise to the strong force that confines the quarks. The force becomes weaker at higher energies, a prediction of the theory that is well confirmed by experiment. The proton is held together by gluon exchange among the quarks. Every 10
–24
seconds or so, a gluon hops between quarks in the proton.
One of the most remarkable discoveries about QCD is that the coupling strength of the interaction of the quarks to the gluons, denoted by
g
, becomes weaker as we push the quarks together to extremely short distances. This is known as “asymptotic freedom.” Conversely, at large distances, the quark-gluon coupling becomes very large. This leads to a strong pull on the quarks, preventing them from being separated and isolated in the lab. It also turns out that, because of this strong coupling, only quantum-bound states that are composed of quarks that have an exact color neutrality—a perfect balance of all three quark colors at any instant in time—can exist. This means we can have only combinations of (
rby
), which are the
baryons
, or (
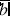
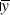 ), which are the
), which are the
anti-baryons
; by ( ) we mean the anti-color of (
) we mean the anti-color of (
q
), or the color-neutral quantum combination of
π
+
↔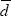 u
u
, which are the mesons. The color gauge theory, QCD, therefore neatly explains the pattern of strongly interacting particles found in nature, and why the quarks can never be really freed from their prisons.