Birth of a Theorem: A Mathematical Adventure (28 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

* * *
No path can be left unexplored when it comes to tracking down new music. Concert listings, online discussion forums, free music sites—and, of course, the wonderful Internet radio station Bide&Musique, which has introduced me to Évariste, Adonis, Marie, Amélie Morin, Bernard Brabant, and Bernard Icher, as well as Stars de la Pub’s fantasy of airplane runways on the Champs-Élysées and Dschinghis Khan’s disco hymn to the glories of Moscow.
Doing mathematics is no different, really. You’re constantly exploring, your eyes and ears are always open, and then every once in a while you’re completely smitten by something and you pour your heart and soul into it, you tell yourself over and over again, hundreds and hundreds of times, that nothing else matters. Well, almost nothing else.
Sometimes the two worlds communicate with each other. Certain pieces of music that have kept me going in the course of a project are forever associated with moments of intense emotion.
When I hear Juliette belting out “Monsieur Vénus,” I see myself again sitting under a skylight in Lyon in the winter of 2006, writing up my contribution to the
Proceedings
of the International Congress of Mathematicians in Madrid, where I was an invited speaker.
“Comme avant,” by the mischievous Amélie Morin, and “Hung Up on a Dream,” by the melodious Zombies, take me back to the summer of 2007 and an apartment in Australia, where I went to learn the regularity theory of optimal transport from the leading experts on the subject—and where I became a fan of the adventures of L, M, and N in
Death Note
,
but that’s another story.…
When Marie Laforêt launches into “Pourquoi ces nuages,” with the incomparable nuances of a voice that is frail and powerful at the same time, I find myself once again in England, at Reading in the winter of 2003, fathoming the mysteries of hypercoercivity.
An untitled song by the fiery Jeanne Cherhal plunges me back into the Probability Summer School at Saint Flour, a small town in the Massif Central in France, where in 2005 I won the Ping-Pong tournament before a cheering crowd.
I listened to Prokofiev’s Second Concerto, whose fourth movement moves me to tears, practically every day during the fall of 1999 in Atlanta while working on my first book on optimal transport.
Mozart’s Requiem! I woke up with it every morning when I was taking the
agrégation
exam in 1994.
And Pär Lindh Project’s “Baroque Impressions,” resounding now and ever more from the depths of a winter’s night following a triumphant plenary lecture at a conference in Reykjavik in January 2005.…
* * *
The hope of discovery and the frustration of imperfection. The proof that remains tantalizingly out of reach. Happiness mixed with pain. The pleasure of feeling alive that songs overflowing with passion go together with so well.
This evening I wasn’t somewhere else. I was alive and well in Princeton, and Ribeiro had to be the one by my side as I worked. Impossible to find her in record stores. Fortunately, there’s the Web: a few songs on her site, also the extraordinary
Long Box
album available via musicMe.
The astounding “Poème non épique” is beyond anything one can imagine—an altogether singular achievement in the history of French chanson. But it’s
too
emotionally charged. My hair stands on end if I so much as think about it, I couldn’t work and listen at the same time.
Instead I chose the magnificent “Jour de Fête.” Power, restraint, emotion, evocative force.
Much rather have been somewhere else
But somewhere else didn’t exist
Then comes my favorite moment, when the voice, calm and controlled until now, suddenly takes flight and begins to make its full power felt—this voice which, as Ribeiro herself says in another song, makes “the dead, the living dead, and the living tremble.”
Didn’t feel like eating or drinking
I wanted to make love
Anywhere anyhow
As long as it’s really love
Even if it’s on the floor
Long as the feeling gets through
Work, Cédric, work. Tea, equations, Ribeiro.
So many sick people that night
Straining so very hard to make it
Sheets tinted a macabre dawn
Smelling, reeking of alcohol
Wow …
Once the song was finished I played it again, and again, and again. I needed this loop, needed to go round and round, in order to leap forward. Work, Cédric, work.
* * *
HOLIDAY
The big day had finally come all right
Festive cheer echoing throughout the night
Behind every window strings of light
Candles gleaming hot like diamonds
’Twas the night before the famous day
We’ve got to celebrate by making
Long, long lines at the cash register
Oh what a tremendous waste that day—
How brightly Paris sparkled that night
But not for me, I wasn’t even there
Me, I’d crossed paths with a satellite
At just the wrong place on my orbit
What the hell was I doing shopping
Stores decked out in all their fake holly
Looking to find some pseudo-rare object
Looking to find some last little surprise—
Much rather have been somewhere else
But somewhere else didn’t exist
Didn’t feel like eating or drinking
I wanted to make love
Anywhere anyhow
As long as it’s really love
Even if it’s on the floor
Long as the feeling gets through—
No calls to answer that night
Phone company’s fault no doubt
Champagne had lost all its taste
Struggled hard to stay awake
Time showed the way to heartbreak
Rain beating on the windowpanes
Nothing could be more pathetic
Hot body in an empty bed—
So many sick people that night
Straining so very hard to make it
Sheets tinted a macabre dawn
Smelling, reeking of alcohol
The Big Day had come—Day of Peace
Rock bottom of my Americas
I was dreaming of my satellite
At just the wrong place on my orbit—

Princeton
April 20, 2009
Teacup in hand, the elderly man turns around and stares at me, not saying a word, visibly taken aback by my rather unusual style of dress.…
* * *
I’m used to people being confused or intimidated by my spider and the clothes I wear. Usually I regard them with benign amusement. But in this case I was at least as intimidated as the person looking at me. For this person was none other than John Nash—perhaps the greatest analyst of the century, my mathematical hero. Born in 1928, he never won the Fields Medal, a failure he bitterly brooded over for decades. Later, of course, he did receive the Nobel Prize for his early work on what soon became known as Nash equilibria, which brought him fame in the fields of game theory, economics, and biology. But what came after this, in the eyes of connoisseurs, was far more extraordinary. It deserved one, or two, maybe even three Fields Medals.
In 1954, Nash introduced the concept of nonsmooth embeddings: monstrosities that made it possible to do impossible things, such as crumpling up a Ping-Pong ball without deforming it, or constructing a perfectly flat ring. In the words of Mikhail Gromov:
It couldn’t be true and yet it was true
—this from a man who understands Nash’s geometrical work better than anyone on earth, and who used it to develop the whole theory of convex integration.
In 1956, proving himself equal to a challenge contemptuously issued by Warren Ambrose, Nash amazed everyone by demonstrating that all the abstract geometries described by Bernhard Riemann—a prince among princes, the Chopin of mathematics—can actually be included (“embedded”) in Euclidean space, the space of our own physical world. In so doing he realized a dream that went back more than a century.
In 1958, in response to a question posed by Louis Nirenberg, Nash demonstrated the regularity of solutions of parabolic linear equations with measurable elliptic coefficients (in physical terms, the continuity in space-time of heat in a completely heterogeneous solid). This result marked the beginning of the modern theory of partial differential equations.
It was fate’s wish that the monastic genius Ennio De Giorgi should solve this last problem at the same time, independently of Nash and by a completely different method. Evidently this takes nothing away from Nash’s remarkable achievement.
Nash may be the only living scientist to have been cast as the hero of a Hollywood film. I didn’t much care for the film myself, but I do have a high regard for the biography by Sylvia Nasar on which it was based. John Nash—a beautiful mind indeed!
If Nash attracted Hollywood’s attention, it wasn’t only on account of his mathematical exploits. It was also because of the tragic story of his life. At the age of thirty he succumbed to paranoid schizophrenia. In and out of psychiatric clinics and hospitals for more than ten years, he seemed fated to live out his days as a pitiable phantom haunting the halls of Princeton, his mind an incoherent ruin.
But then, after three decades of purgatory, Nash miraculously came back from the far shores of madness. Today, more than eighty years old, he is as normal as you or I.
Except that there is an aura about him that neither you nor I have, an aura due to phenomenal accomplishments, strokes of pure genius—and a way of dissecting and scrutinizing problems that makes Nash a model for all modern analysts, myself most humbly among them.
The man who fixed his gaze on me that day is more than a man, he is a living legend. I didn’t have the courage to go talk to him.
But the next time our paths cross I shall dare to approach John Nash. And I shall tell him of my talk on the Scheffer–Shnirelman paradox, which emerged from a proof inspired by his own nonsmooth embedding theorem. I shall tell him of my intention to give a talk on his work at the Bibliothèque Nationale de France. Perhaps I will even tell him that he is my hero. Would he find that ridiculous?
* * *
In the fall of 1956, in New York, a tall, strapping young man pushed open the door to an office in an old factory building just off Washington Square
.
Next to the door, a sign:
INSTITUTE FOR MATHEMATICS AND MECHANICS
.
The visitor’s striking good looks would have given him little reason to envy Russell Crowe, the movie star who was to play him a half century later. His name was Nash, and at the age of twenty-eight he was already famous for his invention of the Nash equilibrium concept and his proof of the embedding theorem, the result of work done first at Princeton and then at MIT. In New York he was to make new acquaintances and discover new problems.
The question put to him by Nirenberg captured his attention at once. It had so far defied some of the best mathematical minds—a worthy adversary!
The continuity of solutions to parabolic equations with discontinuous coefficients.
In 1811 the great Fourier had worked out the heat equation, which governs the evolution of temperature as a function of position and time in a homogeneous solid as it cools:
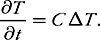
Fourier’s equation subsequently became one of the most distinguished representatives of the class of partial differential equations. These equations describe all the continuous phenomena of our physical world, from ocean currents to quantum mechanics.
