Chris Crawford on Interactive Storytelling (40 page)
Read Chris Crawford on Interactive Storytelling Online
Authors: Chris Crawford

Every Actor’s reaction to an event must include two elements: a choice among the verbs available to the Actor and an emotional reaction that’s an alteration of the Actor’s perceived values. Specifying the inclination formulae for verb choices is an onerous task; specifying the emotional reactions adds to the workload. Fortunately, there’s a way to automatically derive the emotional reactions. The reacting Actor need merely consult the decision script that led to the original verb choice.
Suppose that Fred is considering his options with respect to James, who has just called him a mumbling moron. For simplicity, give Fred just two options: Call James a nattering ninny, or punch James in the face. Suppose further that Fred’s decision is based primarily on hisVirtue: If this variable is negative, he’ll punch James, but if it’s positive, he’ll merely return the insult. Suppose that Fred decides to punch James. Anybody witnessing the event (including James) could examine the inclination formula Fred used to make his decision and infer that Fred’sVirtuemust have been negative for him to have decided to punch James. Therefore, witnesses can adjust theirPerVirtuefor Fred (that is, their perception of hisVirtue) in keeping with this information.
To see how this works, assume that the inclination formulae Fred used in his decision looked like this:
Inclination[Punch] <= Anger[Fred] – Virtue[Fred]
Inclination[Insult] <= Anger[Fred] + Virtue[Fred]
The only difference between the two formulae is theVirtuevariable. You can infer from the formulae thatVirtue[Fred]must be less than zero, but how much less? There’s no way to know—and this is perfectly compatible with dramatic reality. Observing a single case of a person losing his temper doesn’t prove a lot about that person. Therefore, you apply only a gross approximation. In this case, the simplest assumption is thatAnger[Fred] = -5.
 Come on! There’s no foundation for that assumption!
Come on! There’s no foundation for that assumption!
Yes, there is. You know that–10 < Anger[Fred] < 0. I chose the middle value in that range. As I said, it’s a gross assumption, but it’s still a reasonable one given the paucity of data. Besides, I don’t simply substitute this new value for the older value ofPerVirtue[James, Fred]; I average it in with the existing value. I could use a simple averaging:
PerVirtue[James, Fred] <= (PerVirtue[James, Fred] + (-5) ) / 2
Hence, if James’s originalPerVirtuefor Fred was -3, the new value ofPerVirtuewould be:
PerVirtue[James, Fred] <= (-3 + (-5) ) / 2
<= (-8) / 2
<= -4
Or I could use a weighted average representing the fact that this new observation about Fred is only one of many (it uses a 3:1 weighting ratio):
PerVirtue[James, Fred] <= (3 × PerVirtue[James, Fred] + (-5) ) / 4
In this case, James’sPerVirtuefor Fred calculates to:
PerVirtue[James, Fred] <= (3 × (-3) + (-5) ) / 4
<= (-14) / 4
<= -3.5
Or I could get snazzy and keep some sort of weighting factor for each perceived value, denoting the amount of information that has gone into the value. To make it work, I’d have to keep track of the reliability of the current value ofPerVirtue; this is most easily done by counting the number of observations of Fred’s behavior that have gone into the value ofPerVirtue. That reliability factor (PerVirtueReliability) then replaces the weighting factor of 3 used in the preceding formula, as shown here:
For this calculation, say that James has observed Fred’s behavior just twice before; thenPerVirtueReliabilityis only 2 and the calculation looks like this:
PerVirtue[James, Fred] <= (2 × (-3) + (-5) ) / (2 + 1)
<= (-11) / 3
<= -3.66
I would follow up with an increment ofPerVirtueReliability[James, Fred].
I could get even snazzier by using variable increments to an observation’s reliability. When I actually witness an event, I assign high reliability to the value arising from that event. When I am told of an event by another, I give that report a weight proportional to myPerIntegrity(trust in) the reporter. I could give a different weight to a second- or third-person evaluation of Fred’sVirtue(as in “Mary thinks that Fred is an odious cad.”)
The significance of this technique is that it relieves storybuilders of the burden of specifying Actors’ emotional reactions to each event they witness. The act of specifying motivations automatically reveals the character traits that are at work. As Aristotle said, character is revealed by the decisions actors make. This technique is simply the mathematical realization of Aristotle’s dictum.
“My love for you is without measure; it is deeper than the deepest ocean, higher than the tallest mountain, as numberless as the very stars.” So says the romantic lover. Unfortunately, in the world of interactive storytelling you can’t be this poetically extravagant; you have to carry out calculations with these numbers, so you need normal, workable numbers. Each variable you use must have a maximum value and a minimum value.
 Okay, so what should the maximum be? A thousand? A million? A billion?
Okay, so what should the maximum be? A thousand? A million? A billion?
The only consideration in setting a maximum is that you should use a scale most people can easily appreciate. For the average person, thinking in terms of 453,287 love points, for example, is hard. I recommend a maximum value of 1.00, which enables storybuilders to think in terms of percentages, should they be so inclined.
As soon as you create a maximum, you must devise a means of enforcing that maximum. After all, if you decide that the maximum value ofAffectionis 1.00 and then discover that somehow an Actor ended up with anAffectionof 1.20, that will certainly wreak havoc with your algorithms. Ergo, you need some means of enforcing your maximum, which is made difficult by most alterations in these values being incremental in nature. That is, if Fred hasAffectionof 0.38 for Jane, and Jane smiles sweetly at Fred, you need to increase Fred’sAffectionby some small amount. You don’t merely set it to some absolute value because you could end up jerking poor Fred’s emotions all over the map.
Suppose, for example, that Jane smiles sweetly at Fred, which you hold to be worth 0.30Affection, so you set Fred’sAffectionto 0.30. A moment later, Jane fails to laugh at Fred’s lame joke, so you set hisAffectiondown by -0.10. Then she puts her hand on his shoulder to reassure him, and poor Fred’sAffectionjumps back up by 0.50. You need to blend all these events together to integrate them emotionally. You could use a differential system, like so:
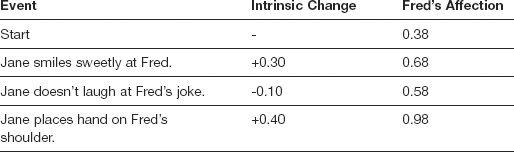
This simple additive system won’t work, however, because it can violate your maximum and minimum values. Suppose you extend the table with a few more events:
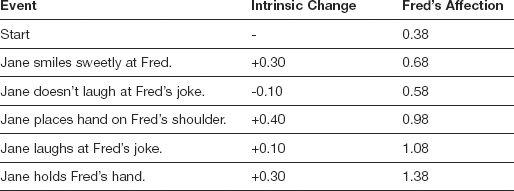
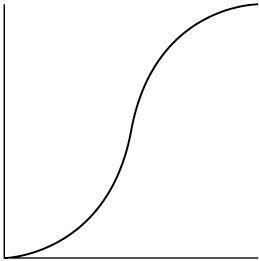
Oops! What now? The solution is to apply a stimulus-response relationship that follows an S-curve, as shown in
Figure 11.2
.