Eight Little Piggies (7 page)
Read Eight Little Piggies Online
Authors: Stephen Jay Gould

A key to understanding these new views may be found in a brilliant paper (see bibliography) on the embryological development of limbs, based on work done just down the hall from my office and published in 1986 by Neil H. Shubin (now at the University of Pennsylvania) and Pere Alberch (now director of the Natural History Museum in Madrid). Shubin and Alberch try to depict the complexity of the tetrapod limb as the outcome of interactions among three basic processes: branching (making two series from one), segmentation (making more elements in a single series), and condensation (union between elements). The limb builds from the body out—shoulder to fingers, thigh to toes. The process begins with a single element extending from the trunk—humerus for the arm, femur for the leg. A branching event produces the next elements in sequence—radius and ulna for the arm, tibia and fibula for the leg. The branching (to wrist bones) sets the distinctive pattern that eventually makes fingers. This key bifurcation is markedly asymmetrical, as one bone ceases to branch (and yields but a single row of segments as the limb continues to develop), while the other serves as a focus for all subsequent multiplication of elements, including the production of digits. Oddly enough, the bone that does not branch is the larger of the two elements—the radius of the arm and the tibia of the leg. The hand and foot are made by branching from the smaller element—the ulna of the arm and the fibula of the leg. (A glance at the accompanying figure should make these anatomical arcana clear.)
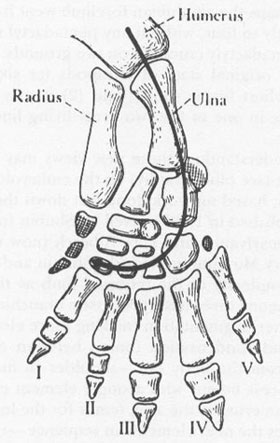
Standard anatomy of a tetrapod forelimb showing the axis of embryological development according to Shubin and Alberch.
From
Basic Structure and Evolution of Vertebrates,
vol. 1, p. 235
.
These basic facts have long been appreciated. Shubin and Alberch make their outstanding contribution in providing a new account of subsequent branching. The classical view holds that a central axis continues from the ulna (or fibula), and that the subsequent branches project from this axis (much like the persistent midvein and diverging lateral veins of a leaf). In this view, the roots of the digits represent different branches. Under this model, largely unchallenged for more than one hundred years, debate focused on the identity of the main axis and its position relative to the digits. T. H. Huxley, for example, argued that the main axis passed through digit three; the British vertebrate paleontologist D. M. S. Watson favored digit four, while the American W. K. Gregory advocated a position between digits one and two.
Shubin and Alberch do not deny the idea of a central axis, but they radically reorient its position. Instead of passing through a particular digit (with remaining digits branching to one side or the other), Shubin and Alberch’s axis passes through the basal bones of
all
the digits in sequence, from back to front (again, a glance at the figure will make this argument clear).
The elegant novelty of this switch may not be evident in the simple change of position for the axis. Consider, instead, the question of timing. Under the old view, one might talk about a dominant digit (focus of the central axis) and subordinate elements (products of increasingly distant branching), but no implications of timing could be drawn. Under Shubin and Alberch’s revision, the array of digits becomes a sequence of timing: Spatial position is a mark of temporal order. Back equals old; front is young. The piggy that “cried wee, wee, wee all the way home” comes first, the one that went to market is last. The thumb and big toe may be functionally most important in humans, but they are the last to form.
As always in natural history, nothing is quite so simple, or free from exceptions, as its cleanest and most elegant expression. Actually, the penultimate digit always forms first—ironically, the piggy that had none—and the sequence then proceeds from back to front with one exception in a reverse branch to digit five. Moreover, this generality meets a fascinating exception in the urodeles (the amphibian group of newts and salamanders, although the other major amphibian lineage of Anura, the frogs, forms digits in the usual back-to-front sequence). Uniquely among tetrapods, urodeles work from front to back (although they also follow the rule of penultimate first, beginning with digit two and then proceeding on towards five). Some zoologists have used this basic difference to argue that urodeles form an entirely separate evolutionary line of tetrapods, perhaps even arising from a different group of fish ancestors. But most (including me) would respond that embryonic patterns are as subject to evolutionary change as adult form, and that an ancestor to the urodele lineage—for some utterly unknown and undoubtedly fascinating reason—shucked an otherwise universal system in tetrapods and developed this “backwards” route to the formation of digits.
But why bring up this innovative model for embryological formation of digits in the context of new data on the multiplicity of fingers and toes in the earliest tetrapods? I do so (as did Coates and Clack in their original article) because the Shubin and Alberch model suggests a simple and obvious mechanism for a later stabilization of five from an initial lability that yielded varying numbers of supernumerary digits. If digits form from back to front in temporal order, then reduction can be readily achieved by an earlier shut-down. The principle is obvious and pervasive: Stop sooner. We can reduce population growth if families halt at two children. You can cut down on smoking or drinking by setting a limit and stopping each day at the reduced number (easier said than done, but the principle is simple enough to articulate). Evolution can reduce the number of fingers by stopping the back-to-front generating machine at five. What we now call digit one (and view as the necessary limit of an invariant archetype) may only be the stabilized stopping point of a potentially extendable sequence.
This perspective makes immediate sense of some old and otherwise unexplained data of natural history. Many lineages in all tetrapod groups reduce the original complement of five to some smaller number—sometimes right down to one, as in horses. As a general principle of reduction, known since Richard Owen’s time, digit one is the first to go. Owen wrote in 1849:
To sum up, then, the modifications of the digits: they never exceed five in number on each foot in any existing vertebrate animal above the rank of Fishes…. The first or innermost digit, as a general rule, is the first to disappear.
Under Shubin and Alberch’s model, the reason behind this rule is obvious: last formed, first gone (the natural analog of the economic maxim: last hired, first fired).
The opposite phenomenon of polydactylous mutations (producing more than five digits) also supports the Shubin and Alberch model. In humans, most polydactylous mutations produce a sixth finger as a simple duplication (subsequent to initial branching) of one member in the usual sequence of five—a phenomenon outside the scope of Shubin and Alberch’s concerns. But, in several other species, the supernumerary elements of multifingered mutants arise by extension as digits continue to form after the branching of digit number one, the usual terminus of the series. J. R. Hinchliffe writes in 1989: “Many polydactylous mutants…have an array of five normal digits, with the supernumerary digits added preaxially [that is, after formation of digit one].” Moreover, Hinchliffe cites some experimental data on inhibition of DNA synthesis during embryology of the lizard
Lacerta viridis
. With less material available for building body parts, digits may be lost. The last-formed digit is always the first to go. Data from both sides therefore support the idea that digits form in temporal series, back to front, and that spatial position is a mark of order in embryological timing: Extra digits are added to, and old digits are lost from, the temporal end-point of the canonical sequence—digit number one.
The pleasure of discovery in science derives not only from the satisfaction of new explanations, but also, if not more so, in fresh (and often more difficult) puzzles that the novel solutions generate. So for the Shubin and Alberch model and our new discoveries on multiplicity of digits in the earliest tetrapods. We used to think of five digits as invariant and canonical, and our chief question was always: Why five? But if five is a secondary stabilization, a stopping point in a temporal sequence with other potential (but unrealized) terminations, we must ask a very different, and in many ways more interesting, question: Why stop at this point? What, if anything, is special about five?
Since five seems to possess a certain arbitrariness under the new views, the tenacity of its stabilization in tetrapods seems all the more enigmatic. The embryological apparatus remains capable of producing more than five (at least in many species), as mutational and experimental data show. But these polydactylous mutations remain as anomalies of individuals or of small and evanescent family lines. They never stabilize within a larger group, and no vertebrate species has more than five digits generated from the back-to-front axis of the Shubin and Alberch model.
The best proof of this assertion lies in apparent (but not actual) exceptions of several tetrapod species with six functional digits. Yes, Virginia, several species do grow six fingers as a rule, not an exceptional state of mutant individuals. Yet this sixth finger is always generated in a different manner and not by the obvious (and apparently easy) mechanics of simple extension past digit one on the Shubin-Alberch series. Frogs, for example, often have six digits on their hind feet (or five on their normally four-fingered front feet). But this extra digit forms in a unique manner by extension of the unbranched sequence of bones leading out from the radius or tibia—the limb bones that never serve as foci for branches and therefore do not (in any other tetrapod species) participate in the production of digits. Anatomists have long recognized the anomalous character of these unique digits by naming them
prepollux
(for the forelimb) or
prehallux
(for the hindlimb). (
Pollux
and
hallux
are technical names for digit number one—our thumb and big toe. Prepollux and prehallux therefore designate an anomalous digit, located in front of the usual front and formed in a different manner.)
A few mammals also possess a functional sixth digit—the panda, whose false “thumb” has been a staple of these essays, and several species of moles. But these false thumbs are formed from extended wrist bones, and are not true digits at all. These facts seem to heighten the oddity (and rigidity) of stabilization at five in a sequence that was once extendable, remains so now for mutations and experimental manipulations, but seems recalcitrant in setting a maximum of five as a normal state in all tetrapod species. When six functional digits form, the extra item must be built in another way.
So why five? Of two major approaches to this question, the conventional Darwinian, or adaptationist, strategy tries to discern a marked advantage, or even an inevitability, for five in terms of utility for an organism’s habitat (an advantage that might promote this configuration by natural selection). A plausible case can be made in terms of benefits for terrestrial life. Creatures that evolve from water to land face many novel challenges, none more severe than the new force of gravity and the consequent need for support in the absence of buoyancy previously supplied by water. The transition from fins to limbs provides the basis for this support, and an old argument holds that five might be an optimal configuration for weight-bearing—a central axis running through on digit three, with adequate and symmetrical buttressing on each side (one or three toes might not provide enough lateral support against wobbling, while seven toes might be superfluous and interfere with locomotion). On this argument, tetrapods have five toes because support and locomotion demand (or at least strongly encourage) this configuration as optimal.
The argument is not implausible, and surely gains credence from the probability that five digits evolved twice on hind limbs—separately, that is, in the two great divisions of tetrapods. The most obvious counterargument may also be support in disguise: Why, if five be best on land, do the earliest tetrapods bear six, seven, and eight toes respectively? A paradoxical retort holds that these first tetrapods evolved their limbs for locomotion in water and remained predominantly, if not entirely, aquatic.
Ichthyostega
, as long recognized, maintained a small tail fin and lateral-line canals on the skull. (Lateral line organs “hear” sound by sensing vibrations propagated through water, a method that does not work in thin air—sec Essay 6.) Coates and Clack’s restoration of
Ichthyostega
and
Acanthostega
limbs add support to this interpretation in a streamlined shape and a limit to rotation that might keep the limb horizontal, in fin position, rather than rotated downward to support a body on land (at least for
Acanthostega
, though the
Ichthyostega
forelimb seems fully load-bearing).
But strong elements of doubt also plague this adaptationist view. First, as stated above, members of one tetrapod lineage, the amphibians, grow but four toes on their front legs, and we have no evidence for an initial five—so pentadactyly may not be a universal stage in terrestrial vertebrates. Second, if five (with symmetry about a strong central toe) be the source of advantage, then why does our favorite species, the traditional measure of all things—
Homo sapiens
—retain five, require great strength in using only two limbs against gravity, but construct the end-member first toe as the main weight bearer?
