Essays in Science (10 page)

A new formulation of the law of inertia had to be found which in case of the absence of a real “gravitational field with application of an inertial system” as a co-ordinate system passed over into Galileo’s formula for the principle of inertia. The latter amounts to this:—A material point, which is acted on by no force, will be represented in four-dimensional space by a straight line, that is to say by a line that is as short as possible or more correctly, an extreme line. This concept presupposes that of the length of a linear element, that is to say, a metric. In the special theory of relativity, as Minkowski had shown, this metric was a quasi-Euclidean one, i.e., the square of the “length” ds of the linear element was a definite quadratic function of the differentials of the coordinates.

If other co-ordinates are introduced by means of a non-linear transformation, ds
²
remains a homogeneous function of the differentials of the co-ordinates, but the co-efficients of this function (gμν) cease to be constant and become certain functions of the coordinates. In mathematical terms this means that physical (four-dimensional) space has a Riemannian metric. The time-like extremal lines of this metric furnish the law of motion of a material point which is acted on by no force apart from the forces of gravity. The co-efficients (gμν) of this metric at the same time describe the gravitational field with reference to the co-ordinate system selected. A natural formulation of the principle of equivalence had thus been found, the extension of which to any gravitational field whatever formed a perfectly natural hypothesis.

The solution of the above-mentioned dilemma was therefore as follows:—A physical significance attaches not to the differentials of the co-ordinates but only to the Riemannian metric co-ordinated with them. A workable basis had now been found for the general theory of relativity. Two further problems remained to be solved, however.

(1) If a field-law is given in the terminology of the special theory of relativity, how can it be transferred to the case of a Riemannian metric?

(2) What are the differential laws which determine the Riemannian metric (i.e., gμν) itself?

I worked on these problems from 1912 to 1914 together with my friend Grossmann. We found that the mathematical methods for solving problem (1) lay ready to our hands in the infinitesimal differential calculus of Ricci and Levi-Civita.

As for problem (2), its solution obviously needed invariant differential systems of the second order taken from gμν. We soon saw that these had already been established by Riemann (the tensor of curvature). We had already considered the right field-equation for gravitation for two years before the publication of the general theory of relativity, but we were unable to see how they could be used in physics. On the contrary I felt sure that they could not do justice to experience. Moreover I believed that I could show on general considerations that a law of gravitation invariant in relation to any transformation of co-ordinates whatever was inconsistent with the principle of causation. These were errors of thought which cost me two years of excessively hard work, until I finally recognized them as such at the end of 1915 and succeeded in linking the question up with the facts of astronomical experience, after which I ruefully returned to the Riemannian curvature.

In the light of knowledge attained, the happy achievement seems almost a matter of course, and any intelligent student can grasp it without too much trouble. But the years of anxious searching in the dark, with their intense longing, their alternations of confidence and exhaustion, and the final emergence into the light;—only those who have experienced it can understand that.

The Cause of the Formation of Meanders in the Courses of Rivers and of the So-Called Beer’s Law

IT IS COMMON KNOWLEDGE
that streams tend to curve in serpentine shapes instead of following the line of the maximum declivity of the ground. It is also well known to geographers that the rivers of the northern hemisphere tend to erode chiefly on the right side. The rivers of the southern hemisphere behave in the opposite manner (Beer’s law). Many attempts have been made to explain this phenomenon, and I am not sure whether anything I say in the following pages will be new to the expert; some of the relevant considerations are in any case known. Nevertheless, having found nobody who thoroughly understood the elementary principles involved, I think it is proper for me to give the following short qualitative exposition of them.

First of all, it is clear that the erosion must be stronger the greater the velocity of the current where it touches the bank in question, or the more steeply it falls to zero at any particular point of the confining wall. This is equally true under all circumstances, whether the erosion depends on mechanical or on physico-chemical factors (decomposition of the ground). We must concentrate our attention on the circumstances which affect the steepness with which the velocity falls at the wall.

In both cases the asymmetry in relation to the fall in velocity in question is indirectly due to the occurrence of a circular motion to which we will next direct our attention. I begin with a little experiment which anybody can easily repeat.

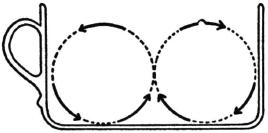
Imagine a flat-bottomed cup full of tea. At the bottom there are some tea leaves, which stay there because they are rather heavier than the liquid they have displaced. If the liquid is made to rotate by a spoon, the leaves will soon collect in the center of the bottom of the cup. The explanation of this phenomenon is as follows:—The rotation of the liquid causes a centrifugal force to act on it. This in itself would give rise to no change in the flow of the liquid if the latter rotated like a solid body. But in the neighborhood of the walls of the cup the liquid is restrained by friction, so that the angular velocity with which it circulates is less there than in other places near the center. In particular, the angular velocity of circulation, and therefore the centrifugal force, will be smaller near the bottom than higher up. The result of this will be a circular movement of the liquid of the type illustrated in
fig. 1.
which goes on increasing until, under the influence of ground friction, it becomes stationary. The tea leaves are swept into the center by the circular movement and act as proof of its existence.

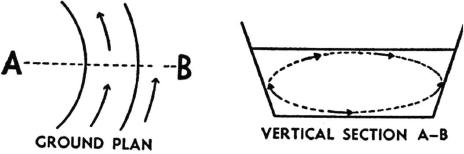
The same sort of thing happens with a curving stream (
fig. 2
). At every section of its course, where it is bent, a centrifugal force operates in the direction of the outside of the curve (from A to B). This force is less near the bottom, where the speed of the current is reduced by friction, than higher above the bottom. This causes a circular movement of the kind illustrated in the diagram. Even where there is no bend in the river, a circular movement of the kind shown in
fig. 2
will still take place, if only on a small scale and as a result of the earth’s rotation. The latter produces a Coriolis-force, acting transversely to the direction of the current, whose right-hand horizontal component amounts to 2 ν Ω sin Φ per unit of mass of the liquid, where ν is the velocity of the current, Ω the speed of the earth’s rotation, and Φ the geographical latitude. As ground friction causes a diminution of this force towards the bottom, this force also gives rise to a circular movement of the type indicated in
fig. 2
.

F
IG
1.

After this preliminary discussion we come back to the question of the distribution of velocities over the cross section of the stream, which is the controlling factor in erosion. For this purpose we must first realize how the (turbulent) distribution of velocities takes place and is maintained. If the water which was previously at rest were suddenly set in motion by the action of an evenly diffused accelerating force, the distribution of velocities over the cross section would be even at first. A distribution of velocities gradually increasing from the confining walls towards the center of the cross section would only establish itself after a time, under the influence of friction at the walls. A disturbance of the (roughly speaking) stationary distribution of velocities over the cross section would only gradually set in again under the influence of fluid friction. Hydrodynamics explains the process by which this stationary distribution of velocities is established in the following way. In a systematic distribution of current (potential flow) all the vortex-filaments are concentrated at the walls. They detach themselves and slowly move towards the center of the cross-section of the stream, distributing themselves over a layer of increasing thickness. The drop in velocity at the containing walls thereby gradually diminishes. Under the action of the internal friction of the liquid the vortex filaments in the inside of the cross section gradually get absorbed, their place being taken by new ones which form at the wall. A quasi-stationary distribution of velocities is thus produced. The important thing for us is that the adjustment of the distribution of velocities till it becomes stationary is a slow process. That is why relatively insignificant, constantly operative causes are able to exert a considerable influence on the distribution of velocities over the cross section. Let us now consider what sort of influence the circular motion due to a bend in the river or the Coriolis-force, as illustrated in
fig. 2
, is bound to exert on the distribution of velocities over the cross section of the river. The particles of liquid in most rapid motion will be farthest away from the walls, that is to say, in the upper part above the center of the bottom. These most rapid parts of the water will be driven by the circular motion towards the right-hand wall, while the left-hand wall gets the water which comes from the region near the bottom and has a specially low velocity. Hence in the case depicted in
fig. 2
the erosion is necessarily stronger on the right side than on the left. It should be noted that this explanation is essentially based on the fact that the slow circulating movement of the water exerts a considerable influence on the distribution of velocities, because the adjustment of velocities which counteracts this consequence of the circulating movement is also a slow process on account of internal friction.

F
IG
2.

We have now revealed the causes of the formation of meanders. Certain details can, however, also be deduced without difficulty from these facts. Erosion will inevitably be comparatively extensive not merely on the right-hand wall but also on the right half of the bottom, so that there will be a tendency to assume the shape illustrated in
fig. 3.

F
IG
3.

Moreover, the water at the surface will come from the left-hand wall, and will therefore, on the left-hand side especially, be moving less rapidly than the water rather lower down. It should further be observed that the circular motion possesses inertia. The circulation will therefore only achieve its maximum extent behind the position of the greatest curvature, and the same naturally applies to the asymmetry of the erosion. Hence in the course of the erosion an advance of the wave-line of the meander-formation is bound to take place in the direction of the current. Finally, the longer the cross section of the river, the more slowly will the circular movement be absorbed by friction; the wave-line of the meander-formation will therefore increase with the cross section of the river.