Finding Zero (7 page)
Authors: Amir D. Aczel

This means that, pretty much, Grothendieck felt he had found a generalization that was so powerful that it allowed him to cast mathematics into any mold he pleased. He could view numbers not as mere numerals and abstract entities, but also as geometrical shapes; he could turn shapes into numerical quantities; equally, he could abstract both of them into entities that lived in highly esoteric mathematical realms that only expert mathematicians
could visualize or understandâand then “do math” in these weird spaces that few have the ability to imagine. While a number is an abstract concept that can be symbolized by a set of signs (the numerals, arranged in various ways), Grothendieck took that abstraction to a whole new level.
It turns out that the mathematics of a topos, invented by Grothendieck, allows for a mathematically consistent and correct basis that justifies the Eastern kind of logic, as explained by Fred Linton.
6
Technically, our strict, either-or logic is necessitated by our reliance on the theory of sets as a basis for mathematics. This gives us the concept of set membership, which is unforgiving: An element is either a member of a set, or it is not; it cannot be both, or neither.
What Grothendieck (with the help of other mathematicians) did was to free mathematics from reliance on set theory and set membership. He employed something called category theory, in which there is no need for sets and membership laws. This freed him to define the topos, within which other logical systems, not requiring the either-or absoluteness, could justifiably exist. Thus it was that through Grothendieck's work, Linton was able to show that Nagarjuna's tetralemma had a perfectly valid mathematical basis. The topos places the Eastern logic with its four possibilities on the same solid foundation as our Western logic. And in the Eastern logic, a ruling concept is that of the void, or emptiness, or nothingness: the zero.
In Linton's topos, applied to the tetralemma, the opposite of “not true” is not the same as “true.” This is the key to the Eastern way of thinking captured by Nagarjuna. In the West, not (not
(true)) = true; this allows us to do proofs by contradiction and captures our strict way of thinking. But in Linton's topos, there is “true,” there is also “not true,” and there is yet a third thing altogether, called “not (not true).” To use Linton's favorite example, this logic applies perfectly in situations in which we say things like “The coffee wasn't unsweet”âmeaning that it wasn't sweet but it was not unsweet either.
This reminds me of an occasion when, a few years ago, my publisher mentioned meeting the publicist they had hired to promote my book. He said, “This person wasn't unattractive.” This is typical of Linton's in-between logic: My publisher didn't want to say the person was attractive, but he didn't want to say unattractive either.
Readers more familiar with fuzzy logic or quantum mechanics, where something can be in a mixture (probabilistic or otherwise) of two seemingly mutually exclusive states, may choose to view the Linton topos in this way. Linton's work proved that the Eastern logic of Nagarjuna and the tetralemma
(catuskoti) has a solid mathematical foundation. Quantum computing, if it becomes a viable reality, may rely on related logical principles that are different from the usual logic we take for granted as the only oneâas my friend C. K. Raju, then back at his university post in Malaysia, recently pointed out to me.
7
And I believe that the logic of the catuskoti is ultimately what led to the invention of the key numeral of our system, the zero.
In India, mathematics and logicâand the intermingling of mathematics and numbers with sexâare very ancient. The earliest known texts in an Indian language are the four collections of religious hymns and rituals, mentioned earlier, known as the Vedas. These were composed in an ancient form of Sanskrit called Vedic Sanskrit, also known as Old Indo-Aryan.
1
The
Rig-Veda
is the oldest of these ancient documents and is believed to have been composed as early as 1100 BCE.
2
This text already displays a tendency toward extensive use of numbers, especially powers of ten. Here are some of its verses:
No bad hymns am I offering by exerting my intellect
In praise of Bhavya ruling on the Indus
Who assigned to me a thousand sacrifices,
That incomparable king desirous of fame.
A hundred gold pieces from the fame-seeking king,
Together with a hundred horses as a present have I received,
I, Kakshivant, obtained also a hundred cows from my master
Who exalted thereby his fame immortal up to heaven.
3
The historian of India John Keay notes that, in the ending verse of this hymn, “by substituting sexual terms for words like âbliss' and âcreation,' it is just possible to grasp” a meaning that made an expert, B. K. Ghosh of Calcutta University, describe this hymn as obscene. We may view it as erotic:
O resplendent lord, with brilliant radiance may you be delighted.
May your own bliss be consummated. Your delightful creation,
The holder of your bliss, is as exhilarating as the bliss itself.
For you, the vigor, equally invigorating is the bliss,
O mighty, giver of a thousand pleasures.
4
We find in the
Rig-Veda
sexual imagery and also extensive use of numbers. According to historian of India John McLeish: “From the time of their earliest civilizations, the inhabitants of the Indian subcontinent had a highly sophisticated awareness of numbers.”
5
McLeish further says that the people of Mohenjo Daroâone of the first known cities on the Indian subcontinent, part of the Indus Valley civilization, which flourished some 4,000 years agoâ“used a simple decimal system and had methods of counting, weighing and measuring that were far more advanced than those of their contemporaries in Egypt, Babylonia, and Mycenean Greece. Vedic altars had to be built to exacting mathematical prescriptions; the correct dimensions and the right geometry were crucial.”
6
It appears that numbers in ancient India were invented for religious purposes very early in human history. While numbers were
of a practical concern in the Westâa necessity of banking, accounting, and everyday purposesâin the East numbers acquired a spiritual, religious meaning.
I read many sources on Indian mathematics. In the 1925 book on the history of mathematics by David Eugene Smith, I found the following:
The early numerals of India are of various kinds. The earliest known forms are found in inscriptions of King Ashoka, the great patron of Buddhism, who reigned over most of India in the third century BC. The characters are not uniform and vary to meet linguistic conditions in different parts of India. Karosthi numerals are simply vertical marks; the Brahmi characters are more interesting. The Nana Ghat inscriptions, from the Nana Ghat cave, 75 miles from Puna, are a century after Ashoka's edicts.
7
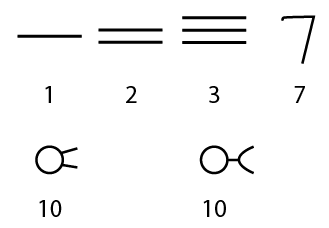
These last numerals from the Nana Ghat inscriptions include a 7 that looks just like our 7, and the 10 looking like the Greek letter
alpha.
They are shown below.

Numerals from the Nana Ghat cave inscriptions, showing 10 and 7 at center.
These appear to be among the earliest numerals that ultimately evolved into the ones we use today. Buddhist monks inscribed them on the wall of a cave high on a mountain in the Western Ghats. They lived in the cave and used it as a place of worship during the second century BCE. We also know that Buddhist travelers throughout Asia were the main conduit for the eventual spread of the base-10 number system across the continent. To visit the cave, one must make the arduous four-hour climb up the steep incline to the bluffs that hide the entrance to this underground Buddhist site. The Indian government has not done enough to preserve it, and the inscriptions bearing numerals that are the progenitors of our number system are now degraded through vandalism and neglect.
But where did the numerals go from there? How did they develop further, after their formulation during the time of Ashoka?
At the National Museum in New Delhi I found a large display explaining the evolution of the letters in Hindi and in other Asian languages. Not far from the display area I saw a working research center. I walked over and began a conversation with two researchers; I was surprised by what one of them said: “We don't like to admit it, but our written language really originates from Aramaic.” This was unexpected. “Well,” the middle-aged scholar wearing a jacket and bow tie continued, “India had long-standing trade relations with the Middle East and with Greece, and Aramaicâthe lingua franca of the ancient Near Eastâinfluenced the development of our own script.”
But I assumed that the numerals could not have come from there, since numbers used in the Near East were either the base-60 Babylonian ones or the Greco-Roman letter-kind of numerals. I
made this observation to the two researchers, and they nodded in agreement and said that perhaps the numerals were indeed a genuine Indian invention, even if the progenitors of the written script had arrived here from the Near East.
In fact, the earliest numerals ever used were in all likelihood Phoenician letters, from which the Hebrew, Aramaic, and other Semitic alphabets evolved.
8
Phoenician is the oldest language in the Near East, and we know that Pythagoras traveled in this region and learned some of his early notions about mathematics from the Phoenicians and the Egyptians and their priests. Our letter
A
and the Hebrew letter
aleph
both derive from the Phoenician letter
aluf,
which means bull and was inspired by a stylized drawing of the head of a bull. This letter once stood for the number 1. As
aleph,
it is still employed in that role by some religious Jews today. As
alpha
, it was used for 1 by the ancient Greeks. The Romans then chose to use I for 1, II for 2, and so on, while the Greeks continued in their own alphabet with
beta
and
gamma
for 2 and 3, and so on, and the ancient Hebrews with
bet
and
gimmel
, and onward.
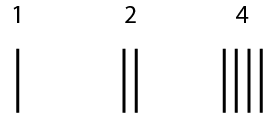
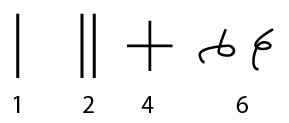
The Kharosthi (top, 3rd c. BCE), Brahmi (middle, King Ashoka's inscriptions, 3rd c. BCE), and Nana Ghat and Nasik Caves (bottom) numerals.
So the Nana Ghat inscriptions are extremely important because they provide strong evidence that our numerals are a genuine Indian invention made during the distant past, and then perhaps developed further while spreading around the world. These numbers were preceded by earlier Indian numerals, the Brahmi script seen in monuments of King Ashoka (slightly different from the Nana Ghat numbers); these, in turn, are related to the Kharosthi script, another alphabet employed in writing Sanskrit and regional
languages starting in the third century BCE in north India and Pakistan.
Noting that all these scripts bearing early numbers are Indian has made experts conclude that our numerals originate in India. But what about the zero?
