Games and Mathematics (18 page)
Read Games and Mathematics Online
Authors: David Wells

9
Convergent and divergent series
The pioneers
The harmonic series diverges
Convergent and divergent series
Archimedes
(287–212 BCE) was the first (known) genius in the history of mathematics. Among his many achievements he anticipated modern calculus and analysis by finding the areas of curves and the volumes of solids with curved surfaces. He was the first mathematician to sum an infinite series in his book
On the Quadrature of the Parabola
.
(287–212 BCE) was the first (known) genius in the history of mathematics. Among his many achievements he anticipated modern calculus and analysis by finding the areas of curves and the volumes of solids with curved surfaces. He was the first mathematician to sum an infinite series in his book
On the Quadrature of the Parabola
.
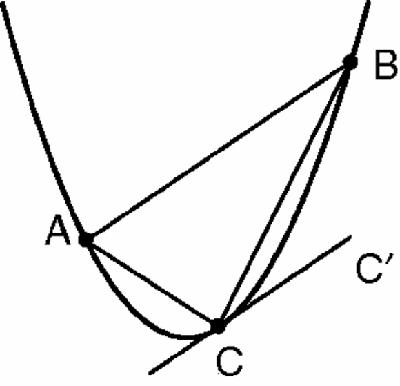
To find the area of the parabolic segment cut off by the line AB he drew the tangent, CC′ which is parallel to AB, to create the triangle ABC (
Figure 9.1
).
Figure 9.1
).
Figure 9.1
Parabola with tangent and triangle
Parabola with tangent and triangle

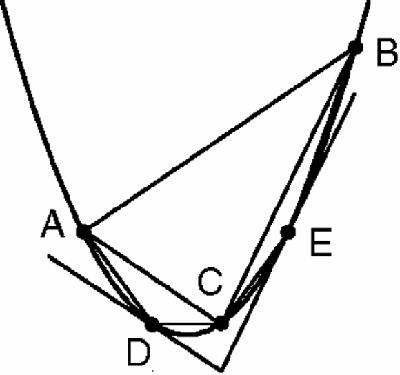
He then drew the tangents at D, parallel to AC and at E, parallel to BC, to create the triangles ACD and BCE (
Figure 9.2
), and proved that the area of each of the two small triangles is 1/8 of the main triangle.
Figure 9.2
), and proved that the area of each of the two small triangles is 1/8 of the main triangle.
Figure 9.2
Parabola with three triangles
Parabola with three triangles

This is already very clever, but now Archimedes produced his master stroke: he imagined drawing the tangents parallel to AD, DC, CE and EB to create 4 more triangles, and then 8 more triangles, and so on. In this way, he argued that the area of the parabolic segment cut off by AB was the sum of all these triangles because when you added all their areas together you would have finally
exhausted
the total area of the parabolic segment.
exhausted
the total area of the parabolic segment.
If we call the area of the triangle ABC, 1, then the total area of the parabolic segment is the sum for this infinite series:
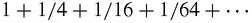 Archimedes got the answer we would expect, 4/3, which was a mystery to other Greek mathematicians who had no idea how an infinite series could have a finite sum.
Archimedes got the answer we would expect, 4/3, which was a mystery to other Greek mathematicians who had no idea how an infinite series could have a finite sum.
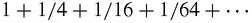
The next remarkable figure in the history of infinite series was the Indian mathematician Madhava
who was born in 1350 at Sangamagramma in Kerala and died in 1425, almost exactly three hundred years before Sir Isaac Newton (1642–1727) and other mathematicians who pioneered infinite series in Europe.
who was born in 1350 at Sangamagramma in Kerala and died in 1425, almost exactly three hundred years before Sir Isaac Newton (1642–1727) and other mathematicians who pioneered infinite series in Europe.
Madhava developed infinite series to represent functions, and he may well have discovered series equivalent to our series for sin
x
, cos
x
and arctan
x
around 1400. Madhava's original works have all been lost, but their substance was preserved by his followers in the flourishing school he founded. Thus when Jyesthadeva wrote his
Yukti-Bhasa
around 1550 he explained one of Madhava's series which is equivalent to James Gregory's series,
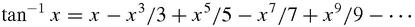
x
, cos
x
and arctan
x
around 1400. Madhava's original works have all been lost, but their substance was preserved by his followers in the flourishing school he founded. Thus when Jyesthadeva wrote his
Yukti-Bhasa
around 1550 he explained one of Madhava's series which is equivalent to James Gregory's series,
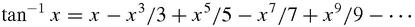
When Madhava put
x
= π/4 he got the series which we call Leibniz's series, but which would more justly be named after Madhava:
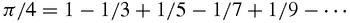 Putting
Putting
x
= π/6 he got the series,
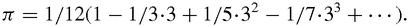
x
= π/4 he got the series which we call Leibniz's series, but which would more justly be named after Madhava:
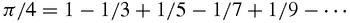
x
= π/6 he got the series,
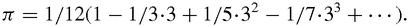
This may be the series that he used to calculate π to 11 decimal places: π = 3.14159265359…[Madhava: MacTutor]. European mathematicians did
eventually catch up. Leibniz used the newly discovered calculus that he had invented at the same time as Newton to find the series for sin
x
, and cos
x
:
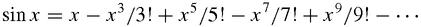 and
and
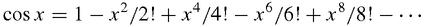 and James Gregory (1638–1675) rediscovered the above series for arctan
and James Gregory (1638–1675) rediscovered the above series for arctan
x
. Newton then discovered the binomial theorem for fractional indices, by analogy with the finite expansion of (
x + y
)
n
when
n
is an integer, and the Europeans were off – but long after Madhava
and the Kerala school had first studied infinite series. (The history of mathematics is not as simple as once thought, and not as purely European.)
eventually catch up. Leibniz used the newly discovered calculus that he had invented at the same time as Newton to find the series for sin
x
, and cos
x
:
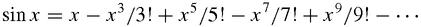
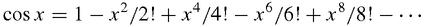
x
. Newton then discovered the binomial theorem for fractional indices, by analogy with the finite expansion of (
x + y
)
n
when
n
is an integer, and the Europeans were off – but long after Madhava
and the Kerala school had first studied infinite series. (The history of mathematics is not as simple as once thought, and not as purely European.)
Nicholas Oresme (1323–1382) has been claimed as the inventor of graphs and coordinates which he used to plot one dependent variable against an independent variable, just as schoolchildren learn to do today [MacTutor: Oresme]. He had no general interest in infinite series but he did prove that the harmonic series,
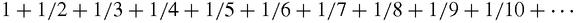 does
does
not
have a sum. It might seem obvious that it must converge to a limit because the terms are getting steadily smaller. Indeed they are, but
not fast enough
. To see why it
diverges
Oresme compared it with another series which definitely diverges:
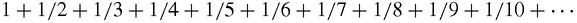
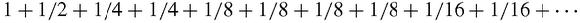
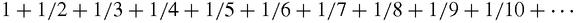
not
have a sum. It might seem obvious that it must converge to a limit because the terms are getting steadily smaller. Indeed they are, but
not fast enough
. To see why it
diverges
Oresme compared it with another series which definitely diverges:
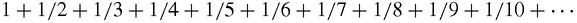
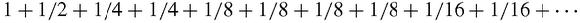
Every term of the harmonic series is equal to or greater than the corresponding term in the second series, all of whose terms can be gathered together like this:
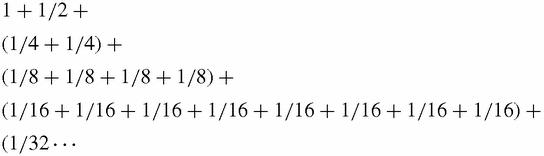
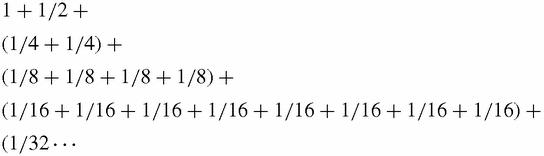
The bracketed groups of terms all sum to 1/2 and the brackets go on for ever so we can add 1/2 as many times as we wish to the running total by adding an extra 2, 4, 8, 16, 32…terms. Because we have to add more and more terms to increase the sum by just 2, it does diverge very slowly indeed, but diverge it does and so does the harmonic series
. How slowly? To get beyond 4 we have to add 31 terms, to get beyond 10, we need 12367 terms, and more than 250000000 terms to pass 20 [Sloane A004080].
. How slowly? To get beyond 4 we have to add 31 terms, to get beyond 10, we need 12367 terms, and more than 250000000 terms to pass 20 [Sloane A004080].
There is another very different way to show that the harmonic series diverges. Suppose that it converges, and that its sum is S. (This turns out to be another case of talking about something which doesn't actually exist.)
Then,
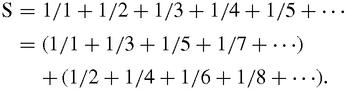
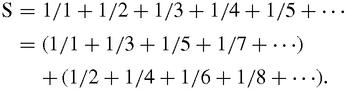
But 1/2+1/4+1/6+1/8+⋯ =
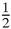 S, and 1/1+1/3+1/5+1/7+⋯ is greater than
S, and 1/1+1/3+1/5+1/7+⋯ is greater than
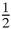 S because each corresponding term is greater. So it follows that S =
S because each corresponding term is greater. So it follows that S =
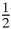 S + a sum greater than
S + a sum greater than
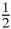 S, which is impossible. So the series cannot be convergent – it must be
S, which is impossible. So the series cannot be convergent – it must be
divergent
.
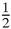 S, and 1/1+1/3+1/5+1/7+⋯ is greater than
S, and 1/1+1/3+1/5+1/7+⋯ is greater than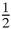 S because each corresponding term is greater. So it follows that S =
S because each corresponding term is greater. So it follows that S =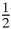 S + a sum greater than
S + a sum greater than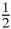 S, which is impossible. So the series cannot be convergent – it must be
S, which is impossible. So the series cannot be convergent – it must bedivergent
.
Other books
Wolf Creek Enforcer by Jo Ellen
Genius by James Gleick
The Officer Says "I Do" by Jeanette Murray
No One Needs to Know by Amanda Grace
The Patron Saint of Ugly by Marie Manilla
His Need, Her Desire by Mallory, Malia
Mail Order Match Maker by Kirsten Osbourne
What a Texas Girl Dreams (Crimson Romance) by Knight, Kristina
B00ARI2G5C EBOK by Goethe, J. W. von, David Luke
Vanished by Liza Marklund
