Games and Mathematics (41 page)
Read Games and Mathematics Online
Authors: David Wells
Formality and mathematics
Hidden mathematics
Style and culture, style in mathematics
The spirit of system versus problem solving
Traditional religion is in decline in much of the developed West, even as mathematics is spreading into every nook and corner. More and more we find mathematicians spotting more-or-less formal aspects of Real Life which on closer examination, and with the application of a little abstraction, can be seen as mathematical. However you think, whatever work you do, whatever problems you are trying to solve, there is a high chance that behind the scenes, underneath the surface, there will be formal, game-like, mathematical structures, by grasping which you will understand the situation better.
It is no accident that mathematics has developed over the last few hundred years in parallel with the realisation that more and more of the world can been seen through mathematical lenses, to be explored scientifically and studied as formal and game-like, and this process is continuing.
The twentieth century was the century of physics and cosmology and chemistry which all depend deeply on mathematics. It has been claimed that this century will be the century of biology – a remarkable turnaround because biology used to be strikingly non-mathematical in contrast to the genuine ‘hard’ sciences. No longer. In the new world of ‘advanced’ biology, mathematics will be present because as biology has progressed it has become more and more apparent that mathematical structures – such as the helical structure of the DNA molecule – underlie biological organisms also.
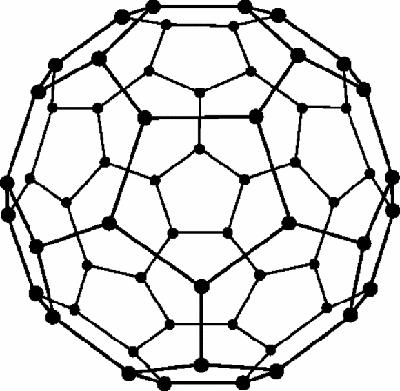
Figure 20.1
is a face-on view of a molecule of Buckminsterfullerene, also known as the Buckyball
or the football molecule, because modern footballs are made with the same surface pattern. It is one of a class of fullerenes, named after Buckminster Fuller, the visionary architect, designer and inventor, whose geodesic domes the molecule resembles. Harold Kroto, Richard Smalley and Robert Curl won the 1996 Nobel Prize for chemistry for discovering this extraordinary object.
is a face-on view of a molecule of Buckminsterfullerene, also known as the Buckyball
or the football molecule, because modern footballs are made with the same surface pattern. It is one of a class of fullerenes, named after Buckminster Fuller, the visionary architect, designer and inventor, whose geodesic domes the molecule resembles. Harold Kroto, Richard Smalley and Robert Curl won the 1996 Nobel Prize for chemistry for discovering this extraordinary object.
Figure 20.1
Buckminsterfullerence molecule
Buckminsterfullerence molecule
The
Buckyball
is also linked to those very early mathematical objects, the Platonic solids. It is not completely regular, because some faces are pentagons while the rest are hexagons. However, all the vertices are identical, composed of 2 regular hexagons and a regular pentagon, and, naturally, the 90 edges, 32 faces and 60 vertices fit the Euler relation.
Buckyball
is also linked to those very early mathematical objects, the Platonic solids. It is not completely regular, because some faces are pentagons while the rest are hexagons. However, all the vertices are identical, composed of 2 regular hexagons and a regular pentagon, and, naturally, the 90 edges, 32 faces and 60 vertices fit the Euler relation.
Regular hexagons themselves only fit together to cover a plane surface. In order to make the shape ‘bend round’ to form a closed surface, pentagons have been added. As it happens, there are an infinite number of closed surfaces, equivalent to the sphere, whose surfaces are made of hexagons and pentagons only, with three faces meeting at every vertex, but in every case, no matter how large or small the total number of faces, the number of pentagons is the same. A puzzle: what is that number? It is no surprise that the answer depends on the Euler relation.
Scientists strive to reveal the underlying mathematical patterns in the world, to make them explicit – often in order to exploit them. There are many other patterns that are created by human beings who have not, however, stopped
to ask questions about them –
unlike mathematicians – but just used them for practical purposes, so that the underlying mathematics has only recently been appreciated. One example is knitting. Ironically, this extremely mathematical activity is usually the province of women and girls and is learned informally at home.
to ask questions about them –
unlike mathematicians – but just used them for practical purposes, so that the underlying mathematics has only recently been appreciated. One example is knitting. Ironically, this extremely mathematical activity is usually the province of women and girls and is learned informally at home.
Aunt Mary did not learn to knit in her arithmetic lessons at school. She learned from her mother or other female relatives as girls have done throughout history not as an irksome task but as a common social activity which has a
play-like aspect: it fills in time pleasantly and so it is re-creational. As laid out in books of knitting patterns, the instructions look extremely algebraic and frankly frightening to a non-expert. This is how to turn a heel:
play-like aspect: it fills in time pleasantly and so it is re-creational. As laid out in books of knitting patterns, the instructions look extremely algebraic and frankly frightening to a non-expert. This is how to turn a heel:
1st row – K.12 [14, 16], sl.1, K.1, psso. K.1, turn.2nd row – P.6 [6, 8], P.2 tog, P.1, turn.3rd row – K. to last 6 [8, 8] sts., sl.1, K.1, psso, K.1, turn.4th row – P. to last 6 [8, 8] sts., P.2 tog., P.1, turn.5th row – K. to last 4 [6, 6] sts., sl.1, K.1, psso, K.1, turn.6th row – P. to last 4 [6, 6] sts., P.2 tog., P.1, turn.
Good heavens! Now I can imagine what a page of ‘elementary’ algebra looks like to a beginning student.
Mysterious
,
weird
, and
frightening
, are three adjectives that come to mind. Yet to those ‘in the know’ who have been initiated into the secret, these instructions are clear, simple and easy to follow. Would that elementary mathematics were so clear to more of its students!
Mysterious
,
weird
, and
frightening
, are three adjectives that come to mind. Yet to those ‘in the know’ who have been initiated into the secret, these instructions are clear, simple and easy to follow. Would that elementary mathematics were so clear to more of its students!
Anthropologists have noted that there are many practices in traditional societies that clearly have a mathematical aspect, though they are ignorant of Western-style mathematics. The mathematics educator Ubiratan D’Ambrosio introduced the term
ethnomathematics
to refer to just such practices and teachers sometimes introduce examples into their classrooms, such as the well-known sand drawings or
sona
, created by the Tchokwe of Angola.
ethnomathematics
to refer to just such practices and teachers sometimes introduce examples into their classrooms, such as the well-known sand drawings or
sona
, created by the Tchokwe of Angola.
As so often happens, the term
ethnomathematics
was at once interpreted differently by different writers – who sometimes had axes to grind. We can say, however, that most of the practices described as ethnomathematics have one feature in common: they are more concerned with
problema
than
theorema
, and do not involve
asking questions about
the practice. That is, they are more practical than theoretical, and so, plausibly, represent a pre-theoretical stage in the development of mathematics, just as chess was more-or-less pre-theoretical prior to Philidor in the eighteenth century.
ethnomathematics
was at once interpreted differently by different writers – who sometimes had axes to grind. We can say, however, that most of the practices described as ethnomathematics have one feature in common: they are more concerned with
problema
than
theorema
, and do not involve
asking questions about
the practice. That is, they are more practical than theoretical, and so, plausibly, represent a pre-theoretical stage in the development of mathematics, just as chess was more-or-less pre-theoretical prior to Philidor in the eighteenth century.
Although formality is everywhere in societies old and new, it appears in many disguises for which people have different preferences. If John enjoys traditional folk dancing and bell-ringing we cannot infer that he will enjoy the related mathematics of group theory. If Mary is an engineer we might be tempted to think that she will appreciate Fourier series which have so many practical
applications – but she may use mathematics purely as an effective instrumental aid, and reserve her real enthusiasm for bridges and roofs.
applications – but she may use mathematics purely as an effective instrumental aid, and reserve her real enthusiasm for bridges and roofs.
We cannot even safely infer that if Peter is a mathematician he will appreciate – let's say – number theory. He may find it quite uninteresting and enthuse instead over differential equations. Just as players prefer different games – Edgar Allan Poe thought draughts much superior to chess – so chess players have different preferences, often linked to different ways of thinking.
‘The style is the man.’ In music, painting, architecture, fashion, reading, politics – you name it – people have their own preferences and styles, and so do mathematicians. Some think visually and geometrically (Klein and Atiyah), some think more algebraically (MacLane), some emphasise experiment while playing games brilliantly (Sylvester), some are adept at both pure and applied maths (Euler and Newton and Gauss), while others are one but not the other (Hardy the purist).
There is a historical factor here: Fermat and Euler and their many brilliant contemporaries were much like naturalists let loose for the first time into a wonderful forest, packed with exotic species: their descendants find the commoner and more brilliantly coloured creatures catalogued and locked up in zoos, and so have to search harder – but successfully – and with brilliant results.
Individual personal differences are easy to accept, if difficult for psychologists to explain. Racial differences are another matter. Felix Klein thought he could detect differences between French and German mathematicians. He claimed in 1893 that ‘a strong native space intuition seems to be an attribute of the Teutonic race, while the critical and purely logical sense is more developed in the Latin and Hebrew races’. At least Klein did not claim that one ‘race’ was superior to the other – merely different. Jacques Hadamard in his book,
The Psychology of Invention in the Mathematical Field
, quoted Klein and then matched Klein's claim with counter-examples from French authors [Hardy
1946
: 114].
The Psychology of Invention in the Mathematical Field
, quoted Klein and then matched Klein's claim with counter-examples from French authors [Hardy
1946
: 114].
Ludwig Bieberbach was a different case. Lecturing in Berlin under the Nazis, he claimed that nationality, blood and race influence the style of mathematics and that there were two types of mathematicians, the J-type, basically Germans, whose mathematics was superior to that of the S-type, who were basically Frenchmen and Jews. Hardy wrote a powerful letter to
Nature
, damning Bieberbach and regretting that he actually seemed to believe such nonsense. [Hardy
1934
: 134].
Nature
, damning Bieberbach and regretting that he actually seemed to believe such nonsense. [Hardy
1934
: 134].
Cultural influences are something else again. Continental mathematicians who followed Leibniz's superior notation and vocabulary for the calculus plausibly had a lasting advantage over British followers of Newton.
The simplest explanation for such cultural contrasts is transmission – students are taught differently by different teachers – but there are more complex explanations. It has been noted, for example, often by Americans themselves, that they are inclined to think in a mechanical manner: the very metaphors of checks and balances used to describe the Constitution have been interpreted as mechanical and a natural development from the original Newtonian model of the universe. Americans are happy to note also that this mechanical ‘genius’ has contributed to their culture in so many ways from Edison's brilliant inventions to their creative enthusiasm for computers and recent successes in Artificial Intelligence. This is clearly a question of
culture
since Americans are a
smorgasbrod
of immigrants from all over the world [Foley
1990
].
culture
since Americans are a
smorgasbrod
of immigrants from all over the world [Foley
1990
].
On the other hand, some differences in style seem to be embedded in the individual personality not the culture. Euclid
set a two-thousand-year-old standard for systematic exposition which was envied by early modern scientists and philosophers who thought that by copying the style of Euclid they could also produce Truth with a capital T. Eighteenth-century critics referred derogatively to the Spirit of System which tried to deduce a vast number of conclusions from a minimal set of premises, a project which outside of geometry they judged to be absurd and impossible.
set a two-thousand-year-old standard for systematic exposition which was envied by early modern scientists and philosophers who thought that by copying the style of Euclid they could also produce Truth with a capital T. Eighteenth-century critics referred derogatively to the Spirit of System which tried to deduce a vast number of conclusions from a minimal set of premises, a project which outside of geometry they judged to be absurd and impossible.
We have already met the Bourbaki
group of French mathematicians. They were system builders
par excellence
. Their guiding ambition was to provide ‘a complete treatment of modern mathematics’ [Felix
1960
: 65]. ‘The organizing principle will be the concept of a hierarchy of structures, going from the simple to the complex, from the general to the particular [Mathias
1992
].
group of French mathematicians. They were system builders
par excellence
. Their guiding ambition was to provide ‘a complete treatment of modern mathematics’ [Felix
1960
: 65]. ‘The organizing principle will be the concept of a hierarchy of structures, going from the simple to the complex, from the general to the particular [Mathias
1992
].
Benoit Mandelbrot, famous for the Mandelbrot set, refers to Bourbaki as an extremist movement which was destroyed by the coming of the ‘rebirth of experimental mathematics, prompted by the arrival of the electronic computer’ [Frame & Mandelbrot
2002
: Chapter
4
]. Alan Bishop also criticised the formality of so much modern mathematics in the Bourbaki mould and gave a list of features he considered
bad
:
2002
: Chapter
4
]. Alan Bishop also criticised the formality of so much modern mathematics in the Bourbaki mould and gave a list of features he considered
bad
:
The experts now routinely equate the panorama of mathematics with the production of this or that formal system. Proofs are thought of as manipulation of strings of symbols. Mathematical philosophy consists of the creation, comparison, and investigation of formal systems. Consistency is the goal. In consequence meaning is debased, and even ceases to exist at a primary level.
In contrast, the phenomenon that was Paul Erdös showed no interest in general systems or in deep abstraction. He was a problem solver and problem poser of genius. However, some of his problems did lead to new fields of mathematics, such as probabilistic number theory (with Mark Kac) and random graphs (with Alfréd Rényi), illustrating how a focus on the specific and contingent leads naturally to the more general and abstract.
The truth – it can hardly be a surprise – is that mathematics depends on both generalists and problem solvers. Bourbaki
upset their opponents not because generality itself is bad – it can be dazzlingly powerful – but because they were extremists. One of the greatest mathematicians of all time illustrates the Middle Way. We have already quoted Hilbert's view that, ‘He who seeks for methods without having a definite problem in mind seeks in the most part in vain.’ Hilbert was a brilliant problem solver with great ambitions. Addressing the
International Congress of Mathematicians
in 1900, he presented 23 problems that in his opinion were the most important unsolved problems at the start of the twentieth century, [Hilbert
1900
] and claimed that:
upset their opponents not because generality itself is bad – it can be dazzlingly powerful – but because they were extremists. One of the greatest mathematicians of all time illustrates the Middle Way. We have already quoted Hilbert's view that, ‘He who seeks for methods without having a definite problem in mind seeks in the most part in vain.’ Hilbert was a brilliant problem solver with great ambitions. Addressing the
International Congress of Mathematicians
in 1900, he presented 23 problems that in his opinion were the most important unsolved problems at the start of the twentieth century, [Hilbert
1900
] and claimed that:
As long as a branch of science offers an abundance of problems, so long is it alive; a lack of problems foreshadows extinction or the cessation of independent development…It is by the solution of problems that the investigator tests the temper of his steel; he finds new methods and new outlooks, and gains wider and freer horizons.
Yet Hilbert also proposed to create a proof theory by which all of mathematics might be formalised and all proofs reduced to calculation in a formal system. It is significant that this project failed – mathematics is not so easily tamed – but by seeing why it failed, we now understand mathematics better.
Other books
Death in Salem by Eleanor Kuhns
Cosmo by Spencer Gordon
The Love Resort by Faith Bleasdale
Rebel Betty by Michaels, Carla
World of Eternia: The Complete Collection by Antony W. F. Chow
False Witness by Uhnak, Dorothy
America's Galactic Foreign Legion - Book 5: Insurgency by Walter Knight
Kill the Dead by Richard Kadrey
Riptide (aka Bluffing Mr. Churchill) by John Lawton
The Sacred Book of the Werewolf by Victor Pelevin
