Games and Mathematics (6 page)
Read Games and Mathematics Online
Authors: David Wells

Chess


‘Chess is the image of war’ [Keene
2006
] but with the blood and gore stripped out to leave only a mental and psychological struggle. The early Persians listed ten virtues enjoyed by the game of chess
. The first, that it nourished the mind, the tenth that it mixed war and sport [McLean
1983
: 113].
2006
] but with the blood and gore stripped out to leave only a mental and psychological struggle. The early Persians listed ten virtues enjoyed by the game of chess
. The first, that it nourished the mind, the tenth that it mixed war and sport [McLean
1983
: 113].
Chess is far more complex than Hex, let alone Nine Men's Morris. There are six different types of pieces and their movements are far richer. The starting arrangement has been determined by history and is highly arbitrary, as are the rule for castling and the modern rules about repetition of moves, so it is extraordinarily difficult to understand and impossible to understand completely.
No one has even tried to prove mathematically either that the first player should win or that it should be drawn with best play or that some specific opening is winning for white, or black.
Players analyse actual sequences of moves as far as they can but deep understanding of tactics and strategy and a creative imagination are necessary to play well. Because the ideas are so subtle and can only be learnt through experience it has taken the greatest players centuries to develop the repertoire of tactical and strategical concepts which now fill thousands of books. Some of the most powerful ideas in the opening were invented, or discovered, as late as the 1950s and 1960s and new possibilities are still being developed, while computer analysis is revealing the secrets of many obscure end-games.
Players learn through experience to spot tactical patterns and develop strategical insight. They conjecture and generalise, then test their theories through play. Reading books, playing over old master games and playing with other players, preferably stronger than yourself, is the best way to pick the brains of better players and speed up the process of developing a subtle and deep intuitive understanding of the game. Like golfers or tennis players or footballers (those games have some abstract features also) developing your chess insight can be a lifelong task.
The extraordinary subtlety of chess explains a curious feature: the vast number of chess variants that have been invented set against the very few that attract serious attention or are played by millions. It is extremely easy to vary any abstract game by simply asking, ‘What if…?’ What if chess were played in three dimensions? What if it were played on a larger board? With pieces with different moves? With two kinds of knights? With the first player making 1 move the second player making 2 moves, the first player 3 moves, and so on? These and scores of other variants have all actually been played. The last is called Progressive Chess and is great fun. It has the added advantage that it usually doesn't last long.
The problem with (almost) all these variations is
depth
. Chess has been played for hundreds of years and over these very long periods deep tactical and strategical ideas have been discovered. Without this depth, there would be no master tournaments, no World Championships and no published collections of masterpieces, and games would never be described as
beautiful
.
depth
. Chess has been played for hundreds of years and over these very long periods deep tactical and strategical ideas have been discovered. Without this depth, there would be no master tournaments, no World Championships and no published collections of masterpieces, and games would never be described as
beautiful
.
It has been well been said that if chess were invented today, it would never take off because players would find it much too hard to get into. It is conceivable that in the future, some powerful computer will be able to quickly analyse a new abstract game, detect a wealth of subtle tactics and deep strategies and so make it so attractive to human players that it will rival chess and Go, but it hasn't happened yet. In the meantime, even an ingenious game like Lasca
, invented by world chess champion Emmanuel Lasker, only has a very modest following and a few enthusiasts.
, invented by world chess champion Emmanuel Lasker, only has a very modest following and a few enthusiasts.
Strategical ideas are especially hard to pin down: there is no doubt that the square in front of a backward pawn is in some sense
weak
, but the meaning of this proverbial fact in
your actual present position
depends on the positions of the other pawns and the play of the pieces.
weak
, but the meaning of this proverbial fact in
your actual present position
depends on the positions of the other pawns and the play of the pieces.
Emmanuel Lasker (1868–1941)Very few mathematicians have been as good at abstract games as they are at mathematics and conversely. Emmanuel Lasker, World Champion from 1894 to 1921, was a bit of an exception although he spent little of his adult life actually doing maths.He did his higher degree under the great David Hilbert, from 1900–1902 after he had already become world champion, spent 1901 as a mathematics lecturer at the Victoria University in Manchester, England, and introduced the concept of a primary ideal which is a generalisation of the idea of a power of a prime number. His most famous paper proved the existence of ‘primary decompositions for polynomial rings’. This is today known as the Lasker–Noether theorem because Emmy Noether, the greatest woman mathematician of all time, proved in 1921 a more general version of Lasker's pioneering work.In 1911 Lasker invented a variant of draughts which he called Lasca and described in a booklet,
The Rules of Lasca, the Great Military Game
[
1911
]. There are two kinds of pieces, Soldiers and Officers, and pieces can be stacked in columns. It was re-published in 1973 by the German games company F.X. Schmid. Later he published a book on board games,
Brettspiele der Volker
[
1925
].Lasker also reached master level at bridge, learnt to play Go and wrote on philosophy – two of his works were translated into English as
Struggle
[
1907
], and
The Community of the Future
[
1940
] – and he became a friend of Einstein who wrote the foreword to his biography by Jacques Hannak. A rare polymath indeed.
Not only is chess very difficult, but almost every position you reach, except for the opening and a few endings, you will have never actually reached before. Consequently, a crucial feature of chess play is the use of analogy: you must exploit your past experience by spotting analogies which ‘ring a bell’,
generalising
your experience and
specialising
your strategical understanding. Of course, analogies can easily let you down if you exploit them uncritically.
generalising
your experience and
specialising
your strategical understanding. Of course, analogies can easily let you down if you exploit them uncritically.
The other side of that coin, of course, is that chess moves can be calculated, move by move, and in theory it is possible to calculate many, many moves ahead, indeed until the end of the game. In practice even the strongest human players find it hard to calculate ahead more than a few moves in most positions because the ‘tree of possibilities’ expands too rapidly, which is why judgement is so important.
Players use their judgement to decide which lines of analysis to pursue in the first place, and then to decide whether a position they believe that they could reach – if their analysis has been flawless – is good for them or for their opponent. Players, in effect, form hypotheses about the position on the board and positions that they could reach in the future, based on a mixture of judgement and analysis of actual moves. The stronger the player, the more likely that their hypotheses are – usually! – more-or-less! – sound.
Figure 2.8
White wins
White wins

So the analysis of particular chess positions is both highly mathematical and analytical, and highly scientific, as well as imaginative. In
Figure 2.8
, (Tartakower-Stumpers, Baarn 1947) there is no practical doubt at all that White,
to play, wins by N-e4 threatening to trap the Black queen by Rb3 and Nc3 or Nc5. The analysis is as sound a proof as any in mathematics, and much simpler than most. In
Figure 2.9
, (Klein-Tartakower, match 1935) however, although it is considered that White should have a larger advantage with four pawns against three than with three against two, which is usually drawn, there is no simple way to prove what the result ought to be.
Figure 2.8
, (Tartakower-Stumpers, Baarn 1947) there is no practical doubt at all that White,
to play, wins by N-e4 threatening to trap the Black queen by Rb3 and Nc3 or Nc5. The analysis is as sound a proof as any in mathematics, and much simpler than most. In
Figure 2.9
, (Klein-Tartakower, match 1935) however, although it is considered that White should have a larger advantage with four pawns against three than with three against two, which is usually drawn, there is no simple way to prove what the result ought to be.
Figure 2.9
An uncertain outcome
An uncertain outcome

Once we start to draw conclusions based not on strict analysis but on concepts such as
strong squares
or a
weak king position
or a
superior pawn structure
, or two bishops against two knights, then we are no longer talking about game-like concepts and we can no longer share our conclusions so easily or communicate them so effectively. The idea of a
strong square
is a scientific concept, not a mathematical one, and a part of the player's scientific understanding. On the other hand, some chess
problems
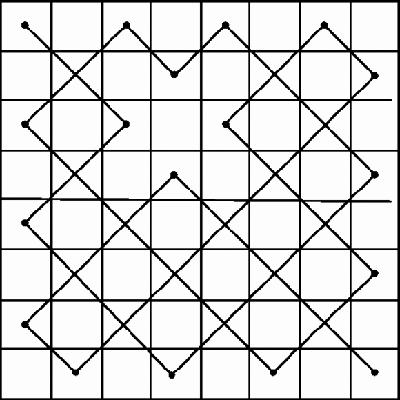
are completely mathematical, such as the task of moving a bishop so that it visits every square of the board (
Figure 2.10
) in as few moves as possible: 17.
strong squares
or a
weak king position
or a
superior pawn structure
, or two bishops against two knights, then we are no longer talking about game-like concepts and we can no longer share our conclusions so easily or communicate them so effectively. The idea of a
strong square
is a scientific concept, not a mathematical one, and a part of the player's scientific understanding. On the other hand, some chess
problems
are completely mathematical, such as the task of moving a bishop so that it visits every square of the board (
Figure 2.10
) in as few moves as possible: 17.
Figure 2.10
Bishop path round 8 by 8 board
Bishop path round 8 by 8 board

The solution, however, like a typical knight tour, is a mixture of pattern and absence of pattern and was constructed by a combination of smart tactics and strategy and trial-and-error [Novcic
1986
: 65].
1986
: 65].
These examples highlight another feature that chess shares with Hex and Go and mathematics, the use of notation. Match and tournament games are recorded and the best are published with annotations. Players also use notation when talking about games without a board: ‘I should have played f4 at once, then if you take, e5 is strong. Nh7 is terrible and if you pin me with Re8 then Qg4 is a double threat.’
When chess is played on a physical board, it is possible to carelessly (or sometimes with malice aforethought) place a piece so that it is half on one square, half on another. When played mentally, using notation, this is not possible, though you could mumble so badly that your opponent cannot clearly hear what you are saying!
Mathematics, of course, has its own notations and language, as well as figures, diagrams and illustrations.
Every legal possibility on the chess board is
forced
by the rules which created the subtlety and richness of all the greatest games of chess ever played, from the masterpieces of the world champions from Steinitz to Fischer to Kasparov, to all the games played by the kibitzers at your local club with all their mistakes and blunders. (When the rules have been changed – they have changed several times since chess was born in ancient India – the tactical and strategical possibilities have changed too.)
forced
by the rules which created the subtlety and richness of all the greatest games of chess ever played, from the masterpieces of the world champions from Steinitz to Fischer to Kasparov, to all the games played by the kibitzers at your local club with all their mistakes and blunders. (When the rules have been changed – they have changed several times since chess was born in ancient India – the tactical and strategical possibilities have changed too.)
These thoughts prompt the question, ‘Are such features of the game of chess invented or discovered?’ Did the
weak squares
in a chess position exist long before they were ‘discovered’? Was the
Sicilian defence
invented by an ingenious Italian, or did it already, as it were, exist as a possibility and he just discovered it? Was the famous smothered mate discovered? Or invented? Plausibly, both: the game of chess and its many variants were invented, they are certainly man-made objects, but their features – as forced by the rules – still had to be
discovered
in practice, a process that took many centuries and which still continues today.
weak squares
in a chess position exist long before they were ‘discovered’? Was the
Sicilian defence
invented by an ingenious Italian, or did it already, as it were, exist as a possibility and he just discovered it? Was the famous smothered mate discovered? Or invented? Plausibly, both: the game of chess and its many variants were invented, they are certainly man-made objects, but their features – as forced by the rules – still had to be
discovered
in practice, a process that took many centuries and which still continues today.
Other books
Where the Shadow Falls by Gillian Galbraith
Guns At Cassino by Leo Kessler
Hunting Evil by Carol Lynne
Salvage the Bones by Jesmyn Ward
Love Without End by Robin Lee Hatcher
Running Dry by Wenner, Jody
The Debt 5 by Kelly Favor
Love by the Book by Melissa Pimentel
Tennessee Williams: Mad Pilgrimage of the Flesh by John Lahr
Filosofía en el tocador by Marqués de Sade
