Life's Ratchet: How Molecular Machines Extract Order from Chaos (10 page)

One day, when Fazio struck his wife in a fit of rage, she hit her head on a table. Fazio regretted his violent act immediately, but Chiara, having grown fond of her unwanted son, Gerolamo, milked the incident for all it was worth. Fainting repeatedly and crying out to her sister who had witnessed the event, she made Fazio promise to let her son attend college. Reluctantly agreeing to this blackmail, Fazio suggested law as it was a lucrative field of study. There was a stipend to be had, and Gerolamo’s father, like many fathers, was eager to get his son an education without having to pay the tuition. Gerolamo, however, did not care about law. He wanted to be a medical doctor, but his father refused to pay for such an expensive course of study. Gerolamo had to find the money somewhere else.

He found it in gambling. Gerolamo preferred playing dice, because he had a natural sense for its probabilities. He did not cheat (a practice not recommended in a time when cheaters often found themselves hanging from the rafters), but he knew how to place bets. Before long, he had saved enough money to pursue medical studies at the renowned University of Padua. After some difficult years, including his annoying his fellow physicians by writing a dissertation about their poor practices, Cardano became a successful physician and chairman of the medical faculty in Padua. He wrote numerous books about medicine and mathematics, especially algebra. And he never forgot his gambling days. Wanting to share his experiences, he wrote the first theory of gambling,
Liber De Ludo Aleae
(“The book on games of chance”).

Although Cardano’s book was not published until a hundred years after it was written, it was a landmark work, introducing the fundamental idea of calculating probabilities: If you wanted to know the probability of a certain event out of all possible events, count the number of ways the event could occur, and divide it by the number of all possible events. This method of calculating assumed that all events were equally likely. Here is an example: What is the probability that you will roll a sum of 5 with two dice? There are 6 × 6, or 36, ways you can roll two dice: (1, 1), (1, 2), . . . (6, 5), (6, 6). How many ways are there to get a sum of 5? Count them up: (1, 4), (2, 3), (3, 2), (4, 1). That’s four ways. Thus, the probability to get a sum of 5 with two rolls of a die is
With some work, you can even work out the probability of a royal flush. Choosing five cards at random out of fifty-two cards provides 2,598,960 different possible hands. Only 4 of these will be royal flushes (one for each suit). Divide 4 by 2,598,960, and you get 1/649,740. You don’t even have to play poker to figure this out.

Cardano makes an interesting hero for our story. As a physician, he understood the chance occurrences that play a role in people’s lives. His life was a jumble of random events. He founded probability theory, invented a method to writing secret messages, and even had a connection to my current hometown of Detroit. He was the inventor of the Cardan shaft, or universal joint, still used in automobiles (and initially designed for a water-pumping system). Sadly, randomness finally got the better of him when a string of bad luck landed him in jail and finally in the poorhouse.

After Cardano, the mathematical treatment of games of chance became commonplace in the seventeenth and eighteenth centuries. Rich (and apparently quite bored) aristocrats sponsored mathematicians to figure the odds of various games. In one such case, the mathematicians Blaise Pascal (1623–1662) and Pierre de Fermat (1601–1665) were commissioned by the Chevalier de Méré to solve the
problem of points
: How should wagers be divided if a game is interrupted too early? Here is the scene: The Chevalier de Méré challenges the Comte de Dubois (a fictitious scenario) to a simple game of dice, and the winner is whoever throws the first 5 sixes. After ten minutes of play, the count is suddenly summoned to meet the king in Versailles. So far, he has thrown 3 sixes, and the knight 4. Neither of them trusts the other. But can the wager of sixteen pieces of gold be fairly divided? Clearly, the wager had to be distributed according to the
probability that either player could still win the game. Pascal decided that this problem was too difficult to solve by himself. He contacted the renowned amateur mathematician Fermat to help him out. Fermat and Pascal corresponded about this problem for a while, until Fermat found a rather tedious way to solve it using Cardano’s simple rule. This inspired Pascal to improve Fermat’s result by devising a general formula, based on a triangle of numbers, now called Pascal’s triangle.

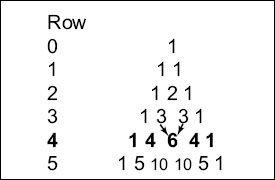
FIGURE 2.1.
Pascal’s triangle. Each number is the sum of the two numbers directly above it. For example, the number 6 in the fourth row is the sum of the two 3’s directly above it (arrows). The numbers represent how many ways you can choose
k
(column) items out of a total of
n
(row) possibilities. This triangle was used by Pascal to solve the problem of points. The fourth row, which is discussed in the text, is highlighted.

The numbers in Pascal’s triangle provide the number of ways you can choose a certain number of items (let’s say
k
items) out of
n
available items
.
An example is the lottery. In a lottery, we pick, say, 5 numbers out of a possible 56, as in the MegaMillion game. In how many ways could we do that? A lot! Let’s first try a simpler example: How many ways are there to select 2 items out of 4 available items A, B, C, and D? To find out, we go to the fourth row in Pascal’s triangle (
Figure 2.1
). This row contains the numbers 1, 4, 6, 4, and 1. These numbers tell us how many ways there are to pick
k
items out of 4 available items (if we had 5 available items, we would need to look at row 5 of the triangle, and so on). The numbers 1, 4, 6, 4, and 1 correspond, from left to right, to picking 0, 1, 2, 3 or 4 items out of 4 available items.

Let’s go step by step: As we move from left to right along the fourth row, the first number in the fourth row is a 1. This number tells us in
how many ways we can select
zero
items out of 4.
Not
selecting an item can only be done in exactly one way (mathematics can be strange). The next number in the row is a 4; it tells in how many ways we can select
1
item out of the 4. Since there are 4 possible items, we have 4 ways to pick 1 of them (i.e., we can pick either A, B, C, or D). It gets interesting (and less obvious) when we pick more than 1 item out of 4. How many ways are there to pick
2
items out of 4? Looking at the next number in the fourth row, there should be 6 different ways to do this. And indeed there are: (A, B), (A, C), (A, D), (B, C), (B, D), and (C, D) (we are not allowing picking the same letter twice).

Now, to find out how many ways there are to pick 5 numbers out of 56 would require us to continue the triangle all the way down to the 56th row. You are invited to try, but you will quickly realize that it is a difficult task. The numbers grow quite large. Fortunately, there is a formula to calculate
any
entry in Pascal’s triangle, without having to draw the triangle. It is called the
binomial coefficient
, given by
n
!/((
n – k
)!
k
!), where
n
is the number of items,
k
is the number of possibilities, and
n
! = 1 · 2 · . . . ·
n
. The expression
n
! is called the factorial of
n
. For example, the factorial of 3 is 3! = 1 · 2 · 3 = 6. For our lottery problem, we find that there are 3,819,816 ways to select 5 numbers out of 56. No wonder I haven’t won the lottery yet.

How do the binomial coefficients help to solve the problem of points? Pascal and Fermat realized that you need to figure out in how many ways each person could still win the game. If the Chevalier de Méré needs only two games to win, and the Comte de Dubois three, what is the maximum number of rounds they need to play until one of the men is the winner? The answer is four rounds (or 2 + 3 − 1 = 4). Why? If the knight wins none or only one game, then the count must have won at least three and is the winner. If the knight wins two or more rounds, the count must have won less than his needed three, and loses the game. Either way, one of them will be the winner.

Now that we know they need to play four more rounds to have a winner, we only have to calculate in how many ways the knight can pick his two wins out of the four rounds. And that is the same problem we just solved: He has six different ways to win (think of our items A, B, C, and D as labels for the four rounds they need to play). If he wins
more
than two
rounds, he also wins the game, so we have to consider those possibilities as well. If he wins
three
rounds, he has four ways of doing so (see Pascal’s triangle), and if he wins all four, there is only one way to achieve this feat. In total, he therefore has 6 + 4 + 1 = 11 ways of winning the game. The count, by contrast, only has 4 + 1 = 5 different ways of winning the game (picking three or four wins out of four rounds). Therefore, if they stop the game before the last four rounds, the ratio of the payout that each of them should receive is 11/5 in favor of the knight (who has more ways of winning the game than the count). If there are 16 pieces of gold left, the knight should get 11 and the count 5.

Around the time Pascal and Fermat solved the problem of points, a salesman of buttons and ribbons, named John Graunt (1620–1674), noticed an interesting pattern in the mortality rolls of London. It seemed that the number of deaths was always about the same every year, even though there were many causes of death and the exact circumstances of each death were unique. When he looked at a large-enough sample—provided by the city of London—Graunt found that individual differences became irrelevant and general patterns emerged. The science of statistics was born.

Statistics has been called the theory of ignorance. It’s an apt description. Statistics is what we do when we face complex situations with too many influencing factors, when we are ignorant of the underlying causes of events, and when we cannot calculate a priori probabilities. In many situations, from the motion of atoms to the value of stocks, patterns emerge when we average over a large number of events—patterns not obvious from looking at individual events. Statistics provides the clues to understanding the underlying regularities or the emergence of new phenomena arising from the interaction of many parts.

The work of Graunt led to the first
life tables
, which gave the probability that a newborn would end up living to a certain age. This was the kind of information life insurance companies needed to make money: If you insured enough people and knew your life tables, you could charge people enough money to make sure you ended up in the black, even if occasionally someone died before his or her time. Life insurance became
well-informed gambling, with probabilities taken from real life. In his book
The Drunkard’s Walk
, Leonard Mlodinow reproduces Graunt’s life table for London in 1662. In the late 1600s, 60 percent of all Londoners died before their sixteenth birthday. Such an awful statistic makes modern-day Afghanistan look like paradise. There, the death rate of 60 percent is close to age sixty. By comparison, the 60 percent death rate in Japan is around ninety years old.

Although statistics emerged from the need to quantify economic and sociological data, it was soon recognized that this new science could benefit the hard sciences as well. Repeated measurements of the same phenomenon, especially in astronomy, were observed in the eighteenth century to follow a law of errors: Errors seemed to obey a universal distribution. However, it was difficult to find the correct mathematical function that would fit the error distributions. After all, every set of measurements only fit the distribution approximately, and the approximation only became good enough to allow guessing the right function after a huge number of measurements. After several false guesses by various eminent mathematicians, the German mathematician Carl Friedrich Gauss (1777–1855), using some of his astronomical data, recognized that the so-called normal distribution seemed to fit the bill.