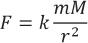Mathematics and the Real World (19 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

Newton's first law
, the law of inertia: Without a force being exerted upon it, a body will continue at a constant velocity.
Newton's second law
: This is best known via the formula
F
=
ma
. In simple language, it says that the acceleration
a
of an object is proportional to the force
F
exerted upon it, and the proportion is determined by the mass
m
of the object.
Newton's third law
: Every force has a reaction. A body that exerts a force on another body will have an equal and opposite force exerted on it by the second body.
The first law is actually derived from the second. Indeed, if the acceleration is zero, the speed is constant. Newton stated this as a law of its own because he saw it as a statement of the existence of “independent” motion, in contradiction to the Aristotelian doctrine that the cause of motion is a force exerted upon a body. Newton gave the appropriate credit to Galileo as the first person to conceive of the idea of inertia. When he was asked to explain the concept of speed itself—in other words, in relation to what, and how does one measure it—he answered that it was measured in relation to the stars that are fixed in the heavens.
The significance of the second law is mathematical, and so is the way to use it. The second law is a differential equation relating the force exerted
on a body to the second derivative of the function of location or position, namely, the acceleration of the body.
The third law is technical and is very confusing. At a luncheon, I once met a senior physician, the head of a department in a well-known hospital; he told me that because of Newton's third law he had stopped studying physics and mathematics. “I decide to push against a wall,” he said; “how can you say that the wall decides to push back at me?” This personification of the situation is indeed confusing, but it misses the purpose of the law, which is basically technical. To illustrate, consider this: A table is standing on the floor. The force of the Earth's gravity is acting upon it. Therefore, according to Newton's second law, the table ought to be falling toward the center of the Earth. It is not falling because of the opposition of the floor. That opposition is translated into the laws of motion in the statement that the floor is exerting a force on the table that is equal in size and opposite in direction to the force exerted on it by the weight of the table. Thus the sum of the forces acting on the table is zero and the table continues to stand, stationary. Another illustration of the third law is rowing. The oarsman pushes the water forward with the oars, in the direction he is facing, and the boat moves in the opposite direction. According to the second law, progress is made due to the force of reaction of the water to the movement of the oars.
Another central law of Newton's, which together with the second law enables much motion to be analyzed, is the law of gravity.
Newton's law of gravity
: All two “point masses” (a point mass is a conceptualized zero-dimension mass) of mass
M
and
m
, respectively, at a distance
r
apart, attract each other with a force that is proportional to their masses and inversely proportional to the square of the distance between them. This can be written in the form of the equation
where
F
is the force, and the coefficient
k
is a constant.
We will state the obvious: Newton did not invent gravity (and the story of the apple is nothing more than a nice story that Newton himself apparently made up to keep troublesome inquirers away). Newton's contribution was the discovery of the
mathematical
relation underlying the law. The Babylonians, and after them the Greeks, had already claimed that the Earth exerts a force that pulls us toward it, and they had coined the word
magnetism
for that force. Formulae similar to that of Newton had been proposed before, and before he had published his law, three leading English scientists, Robert Hooke, Edmond Halley, and Christopher Wren, had discussed the question of what gravitational force would cause the planets to move on elliptical orbits. The three proposed a formula for the force that was similar to Newton's law, but beyond the proposal itself they did not know how to use it. Halley, a friend of Newton's who actually financed the publication of Newton's first book, asked Newton what orbit would be derived from such a formula for gravity and was happy to learn that Newton had already calculated that previously and had found that the orbit was an ellipse. Thus Newton showed that Kepler's first law can be derived from his, Newton's, laws, and shortly thereafter showed that all Kepler's laws can be derived from his own laws. It was the mathematical tools of infinitesimal calculus and differential equations that enabled Newton to formulate his laws of nature and to prove that Kepler's laws could be derived from the new laws.
The new mathematical tool did much more. Galileo described the path along which projected bodies fell on Earth by means of parabolas. Using differential equations, Newton proved that the parabolas resulted from his laws of motion. Here is the essence of the proof (which can be skipped without interrupting the flow of the text).
Newton showed that the derivative of the function
x(t)
=
αt
n
, where
α
is a constant, is
αnt
n
–1
. In particular, if the second derivative has a fixed value
g
, its integral is
gt
, and the integral of the latter is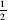 gt
gt
2
. This shows that as the Earth's gravitational pull
g
is constant over short distances; the parabolas that Galileo observed when he dropped bodies from the top of a tower fulfilled Newton's second law of motion.
Newton also examined the oscillations of a spring. The law of restoring force, according to which a spring oscillates, was formulated by Robert
Hooke, who was a bitter opponent of Newton's, and their harsh exchanges of words were well known in British academia. Hooke's law states that the force exerted by a spring is proportional to the spring's deviation from equilibrium. If this rule is applied in Newton's second law, the differential equation that appears in the last paragraph of the previous section, namely,
mx
″ = –
kx
, is obtained. The solution of the equation is also based on differential calculus. The essence of the solution is shown in the next paragraph (again, this can be omitted without interrupting the flow of the text).
Newton's and Leibniz's calculus showed that if
x(t)
=
β
sin(
αt
), where
α
and
β
are constants, then the derived function is
βα
cos(
αt
), and the second derivative is given by –
βα
2
cos(
αt
). We will leave the full proof to mathematicians (and students), but a simple check shows that if we use the notation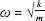 , then both the function
, then both the function
β
sin(
ωt
) and the function
β
cos(
ωt
) solve the differential equation
mx
″ = –
kx
. This shows that the oscillation function is a combination of the sine function and the cosine function.
In this way Newton proved that the empirical finding announced previously by Robert Hooke satisfies Newton's laws. This greatly impressed Hooke, Newton's opponent, and Hooke, despite the adversity between them, complimented Newton in public. Newton reacted with the oft-quoted “If I have seen further, it is by standing on the shoulders of giants.” It is unclear whether the fact that Robert Hooke was short in stature was relevant to Newton's choice of words.
Newton's theory of motion was not readily or widely accepted right away, and many reservations were expressed about the findings. Two astronomical events that occurred many years after Newton's death removed all doubts. The first related to Newton's close colleague, the astronomer Edmond Halley, mentioned above. The paths of comets are affected by the gravity exerted by the larger planets and are therefore difficult to calculate, so much so that scientists expressed doubts as to whether comets also moved in accordance with Newton's laws of motion. Halley studied the trajectory of one comet, whose several appearances in the past had been documented, and he predicted that it would appear again at the end of 1785 or the beginning of 1786. Its appearance in December 1785 significantly
reduced the doubts about the correctness of Newton's equations. Halley was honored by that comet being named after him. Its most recent appearance was in 1986, and it will be visible again in 2061.
The second event resulted from some inconsistencies between observations of the orbits of known planets and the predictions based on Newton's equations. This led to the discovery of a new planet being foretold, and eventually, in 1846, it, the planet Neptune, was discovered in space.
The laws of gravity also provided a satisfactory explanation for the ebb and flow of the tide. The explanation is that the Moon's gravitational pull has an element that is parallel to the surface of the Earth that has no effect on the height of the surface of the sea and an element that pulls toward the center of the Earth (see the diagram). That pull lowers the level of the water on both sides of the Earth so that the water level rises both on the side of the Earth nearest to the Moon and on the opposite, farthest, side (again, see the figure below). This also explains why high tide occurs twice daily, once when the sea is close to the Moon and once when it is on the opposite side of the Earth, farthest away from the Moon. The gravitational attraction of the Sun has the same effect, but because of its distance from the Earth the force is less strong. The ebb and flow of the tide are the results of the combined effect of these forces. There is a difference in the level of high tide at different phases of the lunar month, that is, at new moon and in the middle of the month, when the gravity of the Moon and the Sun reinforce each other, and the periods one-quarter and three-quarters through the Hebrew (lunar) month, when the Sun's gravitational pull reduces the effect of the Moon on high tide.