Read Mathematics and the Real World Online
Authors: Zvi Artstein
Mathematics and the Real World (7 page)
Among the hundreds of thousands of potsherds found, many contain tables and calculations. The calculations include tables with sums of numbers and of squares, tables with interest on loans that may be taken, and even arithmetic exercises showing calculations of compound interest. Clearly these are our interpretations of what is recorded on the potsherds. The writing itself does not include explanations. We can generally assume that there was a commercial need for these calculations, but potsherds were also found with calculations whose purpose is unclear. One potsherd was inscribed with a calculation that in our current notation has of the form
1 + 2 + 2
2
+…+ 2
9
= 2
9
+ (2
9
– 1) = 2
10
– 1.
(The notation for raising numbers to different powers was not used until the sixteenth century, when René Descartes introduced it.) Other similar calculations involving powers were also found. It is clear that the Babylonians knew how to perform calculations involving numbers raised to different powers, but nowhere were explanations or formulae found for performing the calculation. Other potsherds contained calculations of areas and diagonals of rectangles, as well as calculations of the radius of a circle. In the terminology of today, one calculation gave the ratio of the circumference of a circle to its diameter as 3, and in another it was given as . These values are not far from the exact value of
. These values are not far from the exact value of
π
found later, but there is no evidence that the Babylonians knew that the ratio of the circumference of a circle to its diameter was constant or that they tried to prove it. Babylonian mathematics lacks the element of proof, whether rigorous or not.
One of the better-known potsherds found at Nippur is known as Plimpton 322, the number taken from the catalog of potsherds in the collection in
Yale. The completion of the table is shown below; on the original potsherd, the left column is missing.
| (120) | 119 | 169 |
| (3456) | 3367 | 4825 |
| (800) | 4601 | 6649 |
| (13500) | 12709 | 18541 |
| (72) | 65 | 97 |
| (360) | 319 | 481 |
| (2700) | 2291 | 3541 |
| (960) | 799 | 1249 |
| (600) | 481 | 769 |
| (6480) | 4961 | 8161 |
| (60) | 45 | 75 |
| (2400) | 1679 | 2929 |
| (240) | 161 | 289 |
| (2700) | 1771 | 3229 |
| (90) | 56 | 106 |
The potsherd has been dated to 1800 BCE. It is not easy to decipher the writing, but it is generally accepted that apart from three mistakes, which can also be explained as the writer's errors, the potsherd shows the last two numbers of Pythagorean triples, that is, triples of positive integers that fulfill the equation
A
2
+
B
2
=
C
2
. The connection with Pythagoras's theorem (which we will discuss further on) is clear: the equation applies to the two sides and the hypotenuse of a right-angled triangle. We can see that the Babylonians who lived almost four thousand years ago managed to identify a pattern
between numbers, to calculate, and to present Pythagorean triples with very large numbers, proving that they understood the geometric significance of the Pythagorean triples. Potsherds were also found with such exercises as the following: A rod is standing straight against a wall and its top is at a height of 13 cubits; the top slips down by one cubit. What is the distance of the bottom of the rod from the wall? The answer, that is, 5 cubits, is obtained by using the Pythagorean triple 5, 12, and 13. In all the exercises of this sort that were found, it seems that pre-calculated triples were used. There is no evidence of a formula or a method that the Babylonians used to perform these calculations, and no evidence exists that they expressed a hypothesis about the generality of the Pythagorean relation.
In addition to the lack of rigor in formulation and proof, it appears that the Babylonians were not strict about being exact in their calculations. In multiplication tables, mistakes are found that clearly derive from the fact that the writer did not consider precision in the answer to be important. An approximate result that would suffice for all practical purposes was sufficient. Mathematics was a practical tool and not an intrinsically theoretical subject.
The Chinese also developed and used mathematics that was quite advanced in their time. It developed later than Babylonian and Egyptian mathematics but without direct contact with those cultures. Our knowledge of Chinese mathematics is based on Indian writings of the first centuries CE that were copied and probably revised by the Arabs in a later period in the first millennium CE. Both the Indians and the Arabs were aware of the mathematics developed in Babylon and Egypt and later on in Greece, and this should be borne in mind when examining their interpretation of Chinese mathematics. We will consider only one element, and that is the relation between the sides of a right-angled triangle. Similar to the Babylonian texts, illustrated Chinese texts attributed to the twelfth century BCE show many exercises calculating lengths and areas based on the ratios in Pythagoras's theorem. For example, a wooden rod of length 6 cao (a Chinese measure) is up against a wall. The bottom of the rod is moved to 2 cao from the wall. How high will the top of
the leaning rod be from the bottom of the wall? These textbooks show how to find the height at which the top of the leaning rod will touch the wall and give many concrete problems with given numbers. Although it is clear that the writers of the textbooks followed a general system in their writing, there are no indications that they tried to prove that their methods always worked or even that they tried to state their method in general terms.
The Egyptian kingdom dates back to about 4200 BCE, and it ruled under various dynasties until the Greek conquest around the fourth century BCE. There is no direct evidence about mathematics that developed in the early periods of the kingdom, but indirect evidence enables us to draw conclusions about the level of Egyptian mathematics. The construction of the pyramids, for example, required extensive knowledge of geometry and a very highly developed computational ability. The Great Pyramid of Giza, near Cairo, was built around 2560 BCE. Its base is a square, and if we divide the perimeter of the base by twice the height of the pyramid, the answer is remarkably close to
π
. It is unlikely that this proves that the designers of the pyramid left a hint that they knew what
π
was. The construction of the Abu Simbel temple in southern Egypt, on the banks of what is now Lake Nasser, definitely required advanced knowledge of engineering and astronomy. Once a year, in the afternoon hours, the rays of the sun illuminated the statue of King Ramses II. Many people are amazed by the enormous size of the pyramids and wonder how they were built with the resources available to the Egyptians of that time. I personally am not so taken by the huge size of the pyramids. A termite hill today is no less monumental, relative to the size of termites, and from an engineering point of view it is even more complex, as the termites take into account wind directions, the danger of flooding in that area, the need for ventilation in their tunnels, and so on. We understand how evolution developed those building abilities in termites. Due to the time that has passed, we understand less about the building methods of the pharaohs of Egypt, and therefore we admire the results. I have much greater admiration for the ability of the Egyptians to construct such a huge structure and to place the opening to face the sun in such a way that it shines on the statue of the king exactly once a year. Trial and error—the basis of evolutionary
development—is not of much help in building temples with a king's statue exposed to the sun only once a year. It was the Egyptians’ understanding of engineering and the calculations they could perform that brought them to such an impressive intellectual achievement.
Our direct knowledge of Egyptian mathematics is derived from the few papyri that have survived. These too contain a wealth of exercises. Among the better-known papyri is the Rhind papyrus, after the British antiquarian who discovered it in 1858, also called the Ahmes papyrus, after the person, apparently an early Egyptian teacher, who wrote it. The papyrus is housed in the British Museum in London. It contains many mathematical exercises, including additions and equations with several unknowns. The script used by the ancient Egyptians was hieroglyphics, which consists mainly of pictograms (or pictographs, pictures used for writing), which generally represented words but sometimes were used for syllables or letters. Hieroglyphics are usually carved into stone slabs. A simpler, more popular type of writing developed alongside hieroglyphics was the hieratic script, which was written in ink on papyri, and this is what was used for the exercises found on the Rhind papyrus. Hieratic script is written from right to left, like today's Hebrew and Arabic, and numbers are to the base 10, but the position of the digits was not important. Thus, for example, the symbol for ten was ∩, and _ represented four. Hence, the number twenty-eight could be written as _ _∩∩. There were special signs for simple fractions, but there was no sign for addition. When numbers had to be added, they were written side by side, and the reader was expected to understand from the context that they had to be added. We see that the Egyptians’ relation to mathematical texts was similar to the Babylonians’, that is, it was like their relation to language. In other words, there was no need for greater precision in mathematics than in normal written language.
A famous exercise from the Rhind papyrus shows 7 houses, 49 cats, 343 mice, 2,401 sacks of wheat, and 16,807 weights, with the answer given as 19,507. We note that the answer is the sum of 7 + 7
2
+ 7
3
+ 7
4
+ 7
5
. We may conclude also that the Egyptians knew about adding numbers raised to different powers. We do not know how they did it. No general formula is shown for performing this addition or other exercises. The reader or student apparently
had to learn how to solve other problems from the way the examples were solved. The correctness of the solution is not proved either.
The Egyptians’ engineering capabilities also indicate their mathematical abilities in geometry. The papyri also contain exercises for calculating areas. The calculation of the area of a circle enables us to derive the value the Egyptians gave to the ratio
π
of the circumference of a circle to its diameter. In one of the exercises, the value is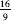 squared, which is approximately 3.16049. This is a fairly close approximation to the correct value. No proof is shown however, nor is there any evidence that the Egyptians knew or even assumed that the ratio of the circumference of a circle to its diameter is constant.
squared, which is approximately 3.16049. This is a fairly close approximation to the correct value. No proof is shown however, nor is there any evidence that the Egyptians knew or even assumed that the ratio of the circumference of a circle to its diameter is constant.
7. AND THEN CAME THE GREEKS
Greek mathematics that developed in what is called the classical period, between about 600 BCE and the rise to power of Alexander of Macedon (i.e., Alexander the Great) in the fourth century BCE, reflected dramatic changes in the approach to mathematics and in the methods of development, analysis, and uses of mathematics. The method formulated in that period served the Greeks themselves in the next few centuries and has remained, almost without change, the dominant system of mathematics until the present. Before we give a brief description of the developments, we should observe that after two thousand five hundred years of learning and using the method introduced by the Greeks, and generations during which we have become accustomed to such a system of analysis and debate, it is sometimes hard to appraise the significance of the dramatic turnaround that took place then. Today, the path paved by the Greeks seems natural and self-evident, but the new ideas are in contrast to what was expected from development in which evolutionary fundamentals were predominant. Greek mathematics constituted a sharp deviation from thousands of years of earlier mathematical activity and put forward an approach that largely contradicted the path dictated by healthy intuition. It is therefore understandable why the process of familiarization with the new ideas, and
the development and incorporation of the method itself, took hundreds of years. This section deals with this aspect of the main developments. The next section will discuss what motivated the Greeks to instigate this revolution in mathematics.

