Pythagorus (11 page)


Or, begin with two pebbles and then set out four, then six, then eight, etc. â all even numbers â and the result is a rectangle.

That is easier to understand visually than verbally, one reason to use pebbles.
Pythagoras and his associates were alert for hidden connections. The pebble figures of the square and rectangle dictated a division of the world of numbers into two categories, odd and even, and this struck them as significant. It was a link with what they were thinking of as the two basic principles of the universe, âlimiting' and âlimitless'. âOdd' they associated with âlimiting'; âeven' with âlimitless'.
Another way of manipulating the pebbles was to cut a triangle from either the square or the rectangular figure.

In the line of pebbles that then forms the diagonal or hypotenuse of the triangle, the pebbles are not the same distances from one another as they are in the other two sides, nor are they touching one another. Having all the pebbles in all three sides of a triangle at equal distances from their immediate neighbours, or all touching one another, requires a new figure: Set down one pebble, then two, then three, then four, with all the pebbles touching their neighbours. The result is a triangle in which all three sides have the same length, an equilateral triangle.

Notice that the four numbers in this triangle are the same as the numbers in the basic musical ratios, 1, 2, 3, and 4, and the ratios themselves are all here: Beginning at a corner, 2:1 (second line as compared with first), then 3:2, then 4:3. The numbers in these ratios add up to 10. The Pythagoreans decided 10 was the perfect number. They also concluded that there was something extraordinary about this equilateral triangle, which they called the
tetractus,
meaning âfourness'. The
tetractus
was, in a nutshell, the musical-numerical order of the cosmos, so significant that when a Pythagorean took an oath, he or she swore âby him who gave to our soul the
tetractus
'.
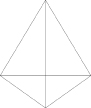
Most scholars think it was after Pythagoras' death that the Pythagoreans found they could construct a tetrahedron (or pyramid) â a four-sided solid â out of four equilateral triangles, and they probably knew this by the time Philolaus wrote the first Pythagorean book in the second half of the fifth century.
[5]
The word
tetractus
, however, was in use during Pythagoras' lifetime. It hints that there was more âfourness' to the idea than the fact that 4 was the largest number in the ratios. The tetrahedron or pyramid is a solid in which each face is a
tetractus,
but which also uses the number 4 in other manners â 4 faces, 4 points.
When Aristotle, in the fourth century B.C., was researching the Pythagoreans, he found a list of connections they made between numbers and abstract concepts. He apparently could not discover what they connected with the numbers 6 and 8.
- Mind
- Opinion
- The number of the whole
- Justice
- Marriage
- ?
- Right time, due season, or opportunity
- ?
- Justice
- Perfect
It is not difficult to understand how Mind might be 1 and Opinion 2. Justice appears twice because of an association with squareness. The Greeks did not think of 1 as a number. âNumber' meant plurality, more than 1. So, for them, the smallest number that is the square of any whole number was 4.
[6]
The first number that is the square of an odd number is 9, and that, too, they associated with justice. The idea that âsquare' means an evened score â with all need for retaliation at an end â still shows up in the colloquial phrase âThat makes us square'. Marriage (5) was the sum of the first odd and even numbers (2 and 3). The link between 7 and âright time' or âdue season' reflected wider Greek thought. Life happened in multiples of 7. A child could be born after 7 months in the womb, cut teeth 7 months later, reach puberty at 14, and (if a boy) grow a beard at 21.
The Pythagoreans followed one line of thought that seems particularly odd today, accustomed as most of us are to thinking of squares and cubes of numbers but not of other geometric shapes possibly connected with them in a similar manner. The âsquare' of 4 was 16, but the âtriangle' of 4 was 10, the perfect number. Both ideas were equally picturable with pebbles.
 Â Â Â Â Â Â Â Â
        
Stacking the pebbles so as to discover that the âcube' of 4 was 64, you might just as easily pile them up another way so that the âpyramid' of 4 was 20. Montessori teaching exploits the delight of playing games like this with little objects like pebbles â in the case of Montessori, beads.
Having come to the conclusion not only that numbers, but the specific numbers 1, 2, 3, and 4 and the ratios between them were the primordial organising principle of the universe, Pythagorean thinking moved in other directions, some of which seem strange and primitive, but it is not surprising that they overestimated the simplicity of the rationality they had glimpsed and were too expectant of immediate applications and results. They were not unlike the earliest followers of Jesus, coming away from what was for them a transforming experience and trying to apply it to the everyday world, thinking all would be resolved soon. The Pythagoreans had discovered a new road to âtruth'. Great thinkers thought about truth and proposed answers. Only a shaman â and many regarded Pythagoras as what we today would call a shaman â was sure he had the answer. In fact, Pythagoras and his followers
did,
but they travelled their new road weighted down with ancient baggage. Still in the age of oracles, divination, and mystic utterances, with its preconceptions about the universe and nature, their naive conception of the world carried over into a naive conception of the power of numbers.
The halcyon days
in Croton lasted thirty years. Iamblichus' biography included long lists of names, which he probably got from Aristoxenus, of Pythagoras' first followers, who sat at his feet, heard his teaching, argued points and worked out problems with him, played with the pebbles, and experimented with the
kanon
and with hanging disks. Was the young physician âAlcmaeon' really one of them? Was there actually a âBrontinus' who was husband and/or father of Theano? Were âLeo' and âBathyllus' real people? And what of the âPythagorean women', about whom nothing is known but their names on these lists? Frustratingly, there is no specific surviving information about how the new coinage affected the economy or, except the story of Milo's defeat of Sibaris, about Pythagorean leadership in Croton and the surrounding territory, what offices the Pythagoreans held, or exactly in what capacity they wielded their power â only that they did wield it and that the results were by most accounts beneficial to the region. What is clear is that in about 500 B.C., three decades after Pythagoras arrived in Croton, hostility among the populace and perhaps a coup within the ranks of his followers brought it all to an end. The information is confused and contradictory, with common themes being others' suspicion that Pythagoras and his followers were either becoming too powerful politically or aspiring to too much power â and, oddly, an unusual respect for beans.
