Pythagorus (20 page)

Geometry, Plato had Timaeus explain, had a detailed role in creation when primordial disorder was sorted into four elements â earth, fire, air, and water â and the creator introduced four geometric figures â cube, pyramid or tetrahedron, octahedron, and icosahedron. These âPythagorean' or âPlatonic' solids are four of the five possible solids in which all the edges are the same length and all the faces are the same shape.
[3]
Each element â earth, fire, air, and water â was made up of tiny pieces in one of those shapes, too small to be visible to the eye.
Plato had Timaeus continue: The four elements and four solids were not the alphabet of the universe. The solids were constructed of something even more basic, two types of right triangles. Plato, through Timaeus, admitted there was room for argument about which triangles were most basic, but he thought he was correct to choose the isosceles triangle and scalene triangle. Both are right triangles.
The isosceles triangle is made by cutting a square into equal halves on the diagonal. Obviously, two isosceles triangles make a square, and squares make up cubes (one of the solids).
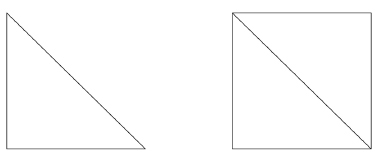
In a scalene triangle, the diagonal is twice as long as the shortest side. Two scalene triangles set back to back create an equilateral triangle â none other than the Pythagorean
tetractus
. The faces of the tetrahedron, octahedron, and icosahedron are equilateral triangles.
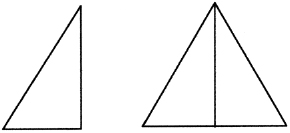
Here is Plato's explanation.
Cube: Fasten together the edges of six squares (each made by pairing two isosceles triangles). The result is a
cube,
the only regular solid that uses the isosceles triangle or square for its construction.
Pyramid or tetrahedron: Fasten together the edges of four equilateral triangles (each made by pairing two right scalene triangles). The result is a
pyramid
or
tetrahedron
.
Octahedron: Fasten together the edges of eight equilateral triangles. The result is an
octahedron
.
Icosahedron: Fasten together the edges of twenty equilateral triangles. The result is an
icosahedron
.
The Pythagoreans and Plato knew the dodecahedron, the only regular solid made of pentagons (12 of them), but Plato did not use it in his scheme.
Beyond those five â cube, pyramid, octahedron, icosahedron, and dodecahedron â there are no other regular solids (polyhedrons). Try to fasten together
any other number
of
any regular figure
(polygon). You get no fit. No wonder the Pythagoreans, Plato, and later Kepler thought these solids were mysterious.
Timaeus explains to Socrates and the other characters in the dialogue that earth is made up of microscopic cubes, fire of tetrahedrons, air of octahedrons, water of icosahedrons. The pairings were based on how easily movable each solid was, how sharp, how penetrating, and on considerations of what qualities it would give an element to be made up of tiny pieces in this shape.
Timaeus pairs the fifth regular solid, the dodecahedron, with âthe whole spherical heaven', and in his
Phaedo,
Plato associated it with the spherical Earth, in spite of the fact that in his time most of the Greek world, except for the scattered Pythagorean communities, still assumed the Earth was flat. The dodecahedron comes close to actually being a sphere. In fact, the earliest mention of a dodecahedron was in sports, with twelve pentagonal pieces of cloth sewn together and the result inflated to create a ball. Each of the five solids fits into a sphere with each of its points touching the inner surface of the sphere, and a sphere can be fitted into each of the solids so as to touch the centre of each surface, which makes sense of Philolaus' enigmatic (and controversial) fragment: âThe bodies in the sphere are five: fire, water, earth, and air, and fifthly the hull of the sphere.'
Though the triangles making up the solids in Plato's scheme may have been the basic âalphabet' of creation, he thought they were not the fundamentals or
archai
. In the dialogue
Philebus
, Socrates says knowledge of the principles of
unlimited
and
limiting
is âa gift of the gods to human beings, tossed down from the gods by some Prometheus together with the most brilliant fire. And the ancients, our superiors who dwelt nearer to the gods, have passed this word on to us.'
3
Plato's contemporaries and generations of later readers thought that by âsome Prometheus', he meant Pythagoras, and that âthe ancients, our superiors who dwelt nearer to the gods', were the Pythagoreans, which contributed substantially to the image of Pythagoras as a channel for superhuman knowledge and wisdom. If Plato meant that, he shortchanged Anaximander, who had talked of âunlimited' and âlimiting' earlier.
According to Plato, one thing that âsome Prometheus' tossed down concerning the unlimited and the limiting was that âall things that are said to be are always derived from One and from Many, having Limit and Unlimitedness inherent in their nature.'
4
He explained this in unpublished lectures at his Academy that Aristotle reported firsthand.
Plato chose to transform the concepts of unlimited and limiting into something slightly easier to understand: unity and plurality. He called these âthe One' (unity) and the âIndefinite Dyad' (plurality). It is easy enough to grasp what is meant by One, or unity, but the Indefinite Dyad is a more difficult concept. Think of it as more than one, or everything that is
not
One, or â more vaguely, but closer to what Plato apparently meant â something implying the possibility of numbers or a role for numbers (there would be no role for numbers if everything were One), but not implying that numbers actually exist. The Indefinite Dyad also implied the possibility of opposites â large/small; hot/cold â for if everything were One, opposites would not exist.
To start things off, the One acted in some fashion upon the Indefinite Dyad and the result was a definite number, 2. The One went on acting on the Dyad, generating the numbers up to 10. Once they existed, the numbers 2, 3, and 4 â numbers in the Pythagorean
tetractus
â predictably played a special role, organising the Dyad to produce geometry. Plato introduced again the progression pointâlineâsurfaceâsolid, connecting the One and the Indefinite Dyad with the world as humans knew it. The meeting of the One and the Indefinite Dyad had been the flashpoint that brought everything else into existence.
On a more mundane level, Plato connected numbers with ideas about an ideal society and ideal rulers. He had probably only recently returned from his first visit to Syracuse when he wrote his
Gorgias
, his earliest dialogue to deal explicitly with political matters. A character named Callicles in the dialogue lusts for power and luxury, and Socrates admonishes him in words that ring with Pythagorean conviction:
Wise men say that heaven and earth and gods and men all are held together by community, friendship, orderliness, self-control and justice, which is why they call this universe a kosmos (a world order, or universe) â not disorderliness or intemperance. But, I fear, you ignore them, though you are wise yourself, and fail to see what power is wielded among both gods and men by geometrical equality. Hence your defence of selfish aggrandisement. It arises from your neglect of geometry.
5
Also in Plato's
Timaeus
, before Socrates relinquishes the floor, he reminds his listeners of two decidedly Pythagorean conditions of âequality' needed for an ideal society: Those whose duty is to defend the community, internally and externally, should hold no private property but own all things in common. Women should share in all occupations, in war and in the rest of life. However, sharing in all occupations did not apparently indicate true equality for women, for later in the same dialogue Timaeus says that if a man fails to live a good life he may be relegated to being a woman in the next.
Archytas had introduced Plato to the Pythagorean quadrivium, the curriculum comprising arithmetic, geometry, astronomy, and music. Plato had Socrates declare, âI think we may say that, in the same way that our eyes are made for astronomy, so our ears are made for harmony, and that the two are, as the Pythagoreans say, sisters of one another, and we agree.' That was Plato's only mention of the Pythagoreans by name, but as Socrates continues he clearly is still talking about them: âThey gave great attention to these studies, and we should allow ourselves to be taught by them.'
Plato was not, however, entirely in agreement with the Pythagorean approach: Studying the stars and their movements was useful insofar as it got one beyond surface appearances to underlying mathematical principles and laws of motion, but, though the stars and their movements illustrated these realities, they never got them precisely right. A philosopher had to go further than what they could show him and attempt to understand âthe true realities, which reason and thought can perceive but which are not visible to the eye'.
6
Plato was convinced that a new manner of education was needed.
Not long after his first visit to Syracuse, Plato had acquired property near Athens that included an olive grove, a park, and a gymnasium sacred to the legendary hero Academus. In that pleasant setting, he had founded his Academy â the name deriving from the legendary hero. For the rest of his life, except for sojourns abroad, he taught there, lectured, and set problems for his students.
[4]
His trainees spent ten years (between the ages of twenty and thirty) mastering the quadrivium, but this was only a preliminary step in Plato's preparation of them to serve as civic leaders who were also philosophers. Education continued in the form of âdialectic'. It is not surprising that Dionysius â in the middle of running an impossibly unwieldy tyranny â balked, though this was the training Plato and Dion felt would enable him to rule effectively.
Forms, in Plato.
Plato spoke of two levels of reality:
- the divine realm of immutable Forms, which is the model for
- the realm in which humans live and where everything is continually changing, ruled by the passions, subject to opinion.
Plato required the dialectic, not merely the quadrivium, because he believed that the world as humans can know it is at best only an imperfect likeness to something else â only a flawed copy of a unique, perfect, eternal model that just âis', âalways is', ânever becomes', and can never change or be destroyed. In the world perceptible to humans, things resembled this higher realm of the âForms' and had the same names, but they were not perfect and eternal.
[5]
They changed â they âbecame'. They began to exist, came to an end, moved about, and were subject to opinions and passions. They were copies or imitations of the Forms; but ânever fully real'.
7
The realm of the Forms could not be perceived by the human senses, but through reasoning and intelligence humans could come nearer to perceiving it. To stretch towards it, Plato thought, you had to use discussion and debate, hence âdialectic'. That was what his characters did in his dialogues â Socrates' question-and-answer lessons â those discussions that never settled anything definitely.
Where did Plato place numbers and mathematics in this picture? Parting company with the Pythagoreans and with Archytas, he thought that although the logic of mathematics and geometry might be part of the universal, immutable truths of the Forms, there was no way humans could find out whether or not they were. Human mathematics was earthbound, deductive reasoning, capable of building only on its own previous knowledge, making the truth of human mathematics only hypothetical, not necessarily Truth with a capital T. In Plato's house, there was no complete staircase from the human-experience level to the level of the Forms. Numbers and mathematics could take you up a few flights. By using dialectic, argument, thought, and logic, you could go higher, but those flights also fell short of reaching the top. You could never find out whether what was up there on the unreachable level was mathematical or not. The Pythagorean house, by contrast, had a complete staircase made entirely of numbers and mathematics. Humans could climb it and, reaching the top, would discover that what was up there was also mathematical. Pythagoreans were sure they knew that mathematics and numbers were the rationality of the universe and the key to complete understanding and reunion with the divine level of reality.
