Pythagorus (35 page)

The philosopher Paul Feyerabend observed that when Copernicus decided to order the heavens he did not consult his ‘scientific forebears', but instead cited a ‘crazy Pythagorean'.
14

In Chapter 10 of Book One of
De revolutionibus
, Copernicus illustrated most fully the new and aesthetically beautiful harmony of his system, revealing in the process how well he knew his Plato, a wealth of other classical literature, and even the work of the Islamic astronomers. Calling attention to the simplicity of the new system, he wrote:

I think it easier to believe this than to confuse the issue by assuming a vast number of spheres, which those who keep Earth at the centre must do. We thus rather follow Nature, who, producing nothing vain or superfluous, often prefers to endow one cause with many effects. . . . So we find underlying this ordination an admirable symmetry in the universe, and a clear bond of harmony in the motion and magnitude of the spheres such as can be discovered in no other wise.
15

The Pythagorean insight, from the sixth century B.C., that harmony and simple pattern expressed in numbers underlie nature clearly was for Copernicus a persuasively strong point in favour of his rearrangement of the cosmos. The potential of numbers, in combination with a preference for harmony and simplicity, to lead to a truer understanding of the universe – a potential that had been poorly exploited by the early Pythagoreans and reinterpreted in many ways, some of them admittedly quite strange, by a great many people since – was finally about to be realised.

Copernicus would not live to see the result of his own Pythagorean dream in print. If he saw a printed copy of
De revolutionibus
at all it was on his deathbed, for he had followed the Pythagorean example of secrecy for years before deciding, finally, to publish. The astronomy he was able to devise in the book turned out to be, in its details, almost as complicated as Ptolemy's, but those few who read it carefully and recognised that Copernicus meant his revolutionary Sun-centred suggestion to be taken seriously, found their minds set on a fresh path indeed. The great Pythagorean insight that had led Copernicus was about to lead younger men out of the Middle Ages and into the modern world.

Others in the
sixteenth century were captivated by the ideas of the Pythagoreans for what might on the surface seem to be entirely different reasons. However, there were deep connections having to do with harmony and numbers.

Architectural trends begun by Vitruvius in antiquity and continued by Alberti in the fifteenth century were brought to their zenith in the sixteenth in the work of one of the most gifted architectural geniuses of all time, Andrea Palladio, whose rise from stonemason to educated architect occurred thanks to an ‘academy' like the one that Marsilio Ficino had established and Lorenzo de Medici had patronised in the fifteenth century at Ficino's villa near Florence. Following Ficino's model, academies had become a part of life in northern Italy; nearly every important town had one. Conscious attempts to re-create Plato's original, they were a combination of boarding school, lecture centre, and attractive location for scholars, intellectuals, and lovers of learning to meet and discuss literature, philosophy, mathematics, and music. The activities often included physical exercise and musical performances. To a surprising extent, social rank was disregarded and talented or clever men of no social standing rubbed shoulders with wealthy aristocrats.

When Palladio was in his early twenties, in the early 1530s, he was hired as a stonemason for a building project near Vicenza. Count Gian Giorgio Trissino, a wealthy humanist scholar and poet, was rebuilding his villa in the classical style to house an academy. Trissino had designed the new buildings himself, and he thought of his design as an interpretation of the work of Vitruvius. Keeping an eye on the progress of the construction, Trissino watched Palladio at work, made a point of getting to know him, and decided that the young man deserved to have a humanist education.

In his famous
I quattro libri dell' architettura
, published in 1570, Palladio would make a deliberate connection with the Pythagorean discovery that certain ratios in music produced sounds that were pleasant to human ears regardless of whether the hearer knew the underlying numbers. ‘Just as the proportions of voices are harmony to the ears,' he wrote, ‘so those of measurement are harmony to the eyes, which according to their habit delight in them to a great degree, without it being known why, save by those who study to know the reasons of things.'
16
For him, the ‘preferred' numbers that would produce such spontaneous delight for the beholder of a building were those based on the same sequences the Pythagoreans had discovered in the ratios of musical harmony: 1 to 2, 2 to 3, and 3 to 4.

In Book I of
I quattro libri
, Palladio chose ‘seven sets of the most beautiful and harmonious proportions to be used in the construction of rooms'. Of course the circle and square were among them. Four others were derived from the Pythagorean musical ratios, and the remaining one was the same room Vitruvius had designed based on Socrates' lesson in Plato's
Meno
, with one dimension of the room being incommensurable. Palladio's seven shapes and proportions were a circle, a square (1:1), a room whose length was the same as the diagonal of the square (1:1.414 . . . etc.), a square plus a third (3:4), a square plus a half (2:3), a square plus two thirds, and a double square (1:2).

Though Palladio devoted only one chapter in the second book of
I quattro libri
to harmonic proportions, and other authors who wrote about him later were more concerned than he, the craftsman, for the theoretical aspects of his work, these Pythagorean proportions were abundantly evident in his drawings.
17
It seemed not to bother Palladio that there were differences between the drawings of buildings and the actual buildings that resulted. If one believed Plato, the Forms were never perfectly realised in the material world.

Andrea Palladio

I quattro libri
was probably the most influential book ever written about architecture. Palladio wrote it in Italian for a lay audience, and Daniele Barbaro, an architectural expert in his own right, for whom Palladio designed the Villa Barbaro in the Veneto near Venice, aptly described it as a complete guide to building from the foundation to the roof. Soon after publication in 1570, the book and its drawings became the rage throughout mainland Europe and, early in the next century, Inigo Jones returned from a trip to Italy and introduced Palladian design to England. Following this ‘first great English Palladian', whose surviving buildings include the Queen's Chapel at St. James's Palace and the Banqueting House at Whitehall, many of England's large country houses were soon being built, or rebuilt, along Palladian lines. Lord Burlington constructed the Assembly Rooms at York on Palladio's designs and fashioned his own home, Chiswick House, after Palladio's Villa Rotonda. Around 1800, Thomas Jefferson designed his Palladian Monticello in Virginia, and numerous American churches of many denominations, university buildings, and official structures and memorials and monuments in Washington, D.C., were following suit, for the feeling was that there was a link between Palladian principles of architecture, with their Pythagorean proportions, and the education, enhancement, and wise governance of society. Palladian design spread to Germany, Russia, Poland, back to Italy, and to Scandinavia.

One of the most unusual houses built using Palladian proportions was the palace-observatory that Tycho Brahe, the finest pre-telescope astronomer, constructed in the latter part of the sixteenth century on the island of Hven in Denmark. As a young aristocrat travelling in Europe, Tycho had visited Venice and the Veneto during the years when Palladio himself was building there, and had probably also seen
I quattro libri
, for he had a connoiseur's appreciation of fine books. Perhaps Tycho was also aware of Palladio's humble origins as a stonemason because, for his own project, he hired a stonemason named Hans van Steenwinkel and raised him to the rank of master builder.

Not everyone who would build in the ‘Palladian' style would pay mind to Pythagorean or Palladian proportions, but Tycho Brahe did. When his ‘Uraniborg' was finished, although it looked at first glance anything but Palladian, the Pythagorean musical ratios were all there and the symmetry extended into the landscape, just as Palladio advised. The portal towers on the east and west sides of the house were each fifteen Danish feet wide and fifteen feet long; the height of the façade was thirty feet, the peak of the roof forty-five feet, the side of the central block sixty feet, giving the ratio 1:2:3:4. The same ratios underlay the dimensions of Tycho's rooms and other elements of the structure. The perimeter wall around Tycho's garden enclosed a square divided by avenues on the diagonal, just as Socrates had divided the squares in Plato's
Meno
. Someone unaware of Tycho's intentions, and not steeped in the architecture of Palladio or on the lookout for Pythagorean ratios, would not have noticed these mathematical and musical subtleties, but Tycho was sure this harmony would make his home and gardens satisfying to the eye and soul, encouraging peaceful, intelligent work and inspiring any sensitive person. Tycho designed and built Uraniborg to be both a palace home and an observatory, all for the purpose of better scrutinising the heavens where the Pythagorean harmony of the spheres – the musical ratios, or perhaps even some deeper harmony – might be discovered. Nowhere else was the Pythagorean and Palladian ideal of proportion so literally, and so idiosyncratically, realised, as in Uraniborg.
18

For complicated reasons involving Danish politics and personal issues, Tycho Brahe eventually abandoned this remarkable, beloved palace, and Denmark, and went into exile – the exile that made it possible for him to meet Johannes Kepler.

CHAPTER 16

‘While the morning stars sang together': Johannes Kepler

Sixteenth and Seventeenth Centuries

As the last decade of the
sixteenth century began, the two-thousand-year-old Pythagorean dream of rationality, unity, and the power of numbers was about to be given a serious test. Pythagoras and his followers had been sure they had caught a glimpse, as through a crack or a keyhole, of truth based on numbers that lay beyond the façade of nature. Johannes Kepler would force the door wide open, once and for all. After him, ironically, and though Kepler did not intend it to be so, the Pythagorean concept of the music of the spheres would survive only in poetic imagery. Yet in a profound and magnificent way, the faith embodied in that concept – faith in a wondrously rational and ordered universe – tempered by Kepler's imaginative genius and rigorous mathematics, would finally place real examples of that music under the feet of science.

The higher seminary at Maulbronn, which Kepler attended in the 1580s as a troubled but exuberantly intellectual and religious teenager, taught ‘spherics' and arithmetic, but it was not until he enrolled at the University of Tübingen that he encountered astronomy. The mission of the Stift at the university where Kepler studied and had his lodgings was to prepare young men for careers of service to the Duke of Württemberg or for the Lutheran clergy, but the course of study was broadly focused. The conviction that there was a unity to all knowledge lived on in the ‘Philippist' curriculum at the great Lutheran universities after the Reformation, as it had in the classical and medieval quadrivium and trivium and in humanist thinking. ‘Philippist' referred to the educational philosophy of Martin Luther's disciple and friend Philipp Melanchthon, who had insisted that one could not truly comprehend and master any part of knowledge unless one comprehended and mastered the whole of it – a sentiment the Pythagorean Archytas would have applauded. Melanchthon felt the church could not succeed in teaching the path to salvation unless it produced a well-read scholarly clergy thoroughly grounded in the liberal arts. Reading the Scriptures, the church fathers, and the classical philosophers required facility in Hebrew, Latin, and Greek. Arithmetic and geometry were necessary for comprehension of both the secular and the sacred aspects of the world, and astronomy was the most heavenly of the sciences. Philippist philosophy also held that since the cosmos was orderly and harmonious, one could, and should, not only observe and record things but also hypothesise about them.

Early in his university career, Kepler realised that theology, mathematics, and astronomy would all be essential in his personal search for truth. He never ceased to be a devoutly religious man, but, as he later wrote, he believed that ‘God also wants to be known through the Book of Nature'. Perhaps it was in that interest (Kepler would have thought so) that God had placed a superb professor of mathematics and astronomy at the University of Tübingen: Michael Mästlin.

Johannes Kepler

When Kepler first arrived there in 1589, forty-six years had passed since the death of Copernicus and the publication of his
De revolutionibus
in 1543. Many scholars were finding Copernicus' grasp of celestial mechanics and his mathematics invaluable, while choosing to ignore his rearrangement of the cosmos. The University of Tübingen still officially taught Ptolemaic astronomy, and Michael Mästlin made sure his pupils had a good grounding in that, for which Kepler would later be grateful when he sought to overturn it. But Mästlin believed that Copernicus' system had to be taken literally and that the planets and the Earth do, indeed, orbit the Sun. Kepler also read Nicholas of Cusa and was soon writing: ‘I have by degrees – partly out of Mästlin's lectures, partly out of myself – collected all the mathematical advantages which Copernicus has over Ptolemy.' In a letter he wrote later to Mästlin, Kepler called Pythagoras the ‘grandfather of all Copernicans'.
8

During his university years, Kepler rapidly became well-read in the classics and also encountered neo-Platonic/Pythagorean thinkers of his own era. He gave all of it a religious and Pythagorean spin of his own: A universe created by God must surely be the perfect expression of a profound hidden order, harmony, simplicity, and symmetry, no matter how complicated and confusing it might appear to people who, like himself, were only beginning to understand it. This was the conviction that set fire to his spiritual and scientific imagination, and that flame would last him a lifetime. He was about to pin this idea to the wall using more precise observations of the heavens and his innate genius for rigorous mathematics: a potent combination.

While still a student at Tübingen, Kepler openly defended Copernican astronomy in two formal debates, arguing that the planets' periods and their distances from the Sun made far better sense in the Copernican system; and that if the Sun was indeed (like the Creator) the source of all change and motion, then it might follow that the closer a planet was to the Sun, the faster it would travel. He worked busily and happily on astronomical questions and wrote a piece about how the movements of the heavens would appear to someone on the Moon. Despite all that, it seems not to have occurred to him that he might pursue any career other than as a clergyman.

Near the end of his fifth university year, Kepler learned that his time at Tübingen was to end immediately, and not in the way he had planned. A Protestant school in southern Austria appealed to the university for a teacher, mainly for mathematics but also with knowledge of history and Greek. Tübingen had decided to send Kepler. Sorely discouraged and frustrated, he made the move to Graz. It was there that, about a year after his arrival, while drawing a diagram on the board for his pupils, he made the startling discovery that a triangle seemed somehow to be dictating the distance between the orbits of Jupiter and Saturn. The triangle was the Pythagorean
tetractus
.

The date was 19 January 1595, and Kepler was lecturing about the Great Conjunctions that occur when Jupiter and Saturn, as viewed from the Earth, appear to pass each other. This does not happen often in anyone's lifetime, for Jupiter overtakes Saturn only approximately every twenty years. Imagine the two planets moving on a great circular belt around the Earth. During the twenty-year interval between two Great Conjunctions, Saturn moves about two thirds of the way around the belt, while Jupiter makes one complete revolution and two thirds of another. The locations of the Great Conjunctions leap forward on the belt by two thirds of the circle every twenty years.

Kepler had drawn a circle on the chalkboard to represent the great circle of the zodiac belt, and then marked the points in the zodiac where the successive Great Conjunctions occurred, viewed from Earth. If one plotted only three Great Conjunctions, those points were very near to being the corners of an equilateral triangle, but not quite. Beginning another triangle where the first ended (plotting the next conjunctions), the new triangle did not precisely retrace the first one. For example, the fourth conjunction in Kepler's drawing (the conjunction that occurred in the year 1643) happened at almost the same point as the first (in 1583), and the fifth at almost the same point as the second. Draw lines connecting them and you almost have an equilateral triangle . . . but, again, not quite, and you have not retraced the first triangle. So the triangle ‘rotates', as Kepler's diagram shows. The result is two circles, outer and inner, with the distance between them set by the rotating triangle. Thus, Kepler's triangle seemed to be mysteriously dictating the distance between the orbits of the first two planets. Interestingly, the radius of the inner circle looked as though it were half that of the outer circle, and observations of the heavens showed that the radius of Jupiter's orbit was approximately half the radius of Saturn's.

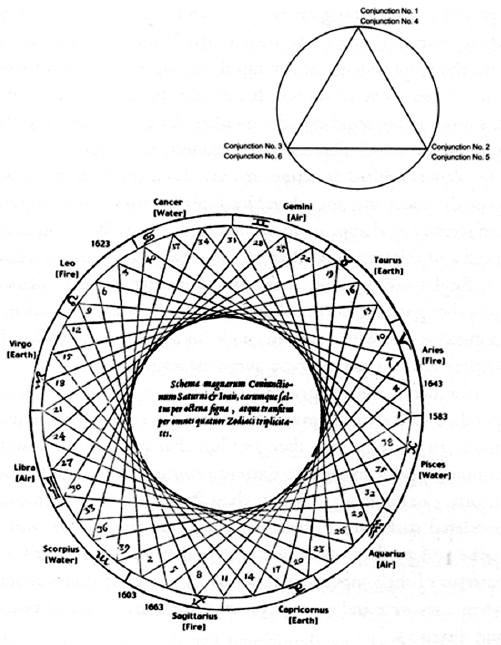
Drawing from Kepler's
Mysterium cosmographicum
depicting the pattern of Jupiter-Saturn conjunctions and where they happened in the zodiac. The conjunction in 1583 (right) occurred when the two planets were in Aries/Pisces. The conjunction in 1603 (lower left) was in Sagittarius, in 1623 in Leo, in 1643 in Aries, in 1663 in Sagittarius, and so on. If the conjunctions occurred repeatedly in the same positions in the zodiac, Kepler's drawing would have looked like the insert (upper right). Instead they ‘progress', as represented in the central figure.

An amazed Kepler decided immediately to try the next regular polygon – the square (the triangle has three sides, the square four) – to see whether it would serve similarly for the separation between the orbits of Jupiter and Mars.
[1]
If it did, he planned to try a pentagon (five sides) for the separation between the orbits of Mars and Earth, a hexagon for Earth and Venus, and so forth. He hoped the arrangement of the cosmos would resemble this diagram, with the triangle, then the square, then the pentagon, then the hexagon, and so forth, all nested between the separate planetary orbits. The idea failed on the first try, when the square would not work for the known separation between the orbits of Jupiter and Mars.

Kepler experimented with other regular polygons, searching for a fit, but he realised that given the infinite number of polygons available, success was assured. To the early Pythagoreans, this might have seemed adequate. Not to Kepler, for the question remained, why – among all the possibilities –
these
particular polygons worked and not others. Why had God chosen to construct the universe in this way and not in some other?

Though many of his contemporaries considered questions like these naive, they bothered Kepler, who had already been focusing his thinking along two lines of investigation: what reasoning God was using when he made things the way they are; and the physical reasons why the universe operates as it does. Clearly, for Kepler, shuffling through all the polygons and finding five that fit neatly between the six planetary orbits was not satisfactory. Since there were regular polygons to fit any planetary distances one might find, he felt there had to be a scheme that would
limit
the actual, possible ratios (Saturn to Jupiter, Jupiter to Mars, Mars to Earth, Earth to Venus, Venus to Mercury), accounting for why some ratios, not others, existed in the heavens and there were only six planets.

It occurred to Kepler that he was making a mistake in trying to apply two-dimensional, flat figures (polygons) to a three-dimensional universe, and he decided to experiment instead with solid figures, the regular polyhedra.
[2]
That thought was a Pythagorean knockout. There were, after all, only five regular polyhedra (the Pythagorean or Platonic solids) not an infinite number of possibilities. To Kepler's immense satisfaction, he found he could fit the five polyhedra into a nested arrangement that quite nicely coincided with the known separations between the six ‘spheres' in which the planets orbit.
[3]