Secrets of Antigravity Propulsion (13 page)

Figure 3.5.
Typical plot showing how thrust and current vary with vacuum pressure for an electrohydrodynamic thrust device.
(Sketch provided by T.
T.
Brown to A.
Wagner)
Because the rate of ion flux passing between the electrodes of the device correlates with current, the ion wind should accordingly have dropped precipitously with the drop in current.
Hence, the data clearly demonstrate that the source of the observed thrust is due not to ion wind, as critics often charged, but rather to some other force.
This raises a question in regard to the canopy pressure measurements described in chapter 2.
In the vacuum chamber tests, there would have been no vortical ion movement below the positive electrode, nor any air-induced pressure differential of the sort proposed in explaining the operation of the aero-marine vertical takeoff vehicle.
The suggestion in the “Electrohydrodynamics” report that the upward thrust results from “electrostatic field stresses” is explored later in this chapter.
Another test, presumably carried out with a larger electrode and energized at a higher voltage, achieved even greater thrusts:
Laboratory devices weighing 100 grams (approx.
3.5 ounces) less power source have produced a thrust of 110 grams, for an electrical power expenditure of 500 watts (250,000 volts @ 2.0 milliamperes).
This experiment was performed in air (1 atmosphere).
Supplementary research indicates much greater efficiency results (same thrust for less power input) when operated in a vacuum (10
-4
mm Hg or better), when the current drops to about 2.0 microamperes.
16
Here, the report makes the astounding disclosure that under hard vacuum conditions, a force of 110 grams (1.1 newtons) could be achieved for a power expenditure of just 0.5 watt (250,000 volts times 2 × 10
-6
amps), or 2,200 newtons of thrust per kilowatt.
This is about 150 times the thrust-to-power ratio of a jet engine!
Also, it is 10,000 times greater than the thrust-to-power ratio of a space shuttle main engine.
The report notes that under harder vacuum conditions of 10
-12
mmHg, such as exist in space, Brown’s electrokinetic propulsion device would be expected to achieve even higher efficiencies due to a further reduction in ion leakage power consumption.
The report also compared the observed thrust with that of the National Aeronautics and Space Administration’s (NASA) ion propulsion engine, which weighed ten times as much as Brown’s saucer and produced only 28 grams of force for an input power of 1,200 watts, or just 0.23 newton per kilowatt.
Hence, NASA’s ion propulsion engine was 10,000 times less efficient than Brown’s electrokinetic disc.
These measurements of thrust indicated that the force lifting Brown’s electrified disc was almost 100 million times greater than what could reasonably be generated by an ion wind.
For example, an upward thrust of 110 grams is equivalent to a force of about 10
5
dynes.
By comparison, a 2-microampere ion wind resulting from electrons accelerated in a 250-kilovolt potential would yield a force of somewhat over 10
-3
dynes, almost 100 million times less than the lift produced by Brown’s apparatus.
Ion Wind Force
The upper-limit estimate for ion wind force may be arrived at through the following calculation: An electron current of 2 x 10
-6
amps would comprise an ion wind flux of
Ф = 1.25 x 10
1
3
electrons per second.
A voltage drop of 250,000 volts would accelerate these particles to a velocity v = 2.96 x 10
1
0
cm/sec, or 0.988c, which would yield a Lorentz factor of γ = 6.6.
The ion wind force, or electron momentum flux, would equal F = 9.1 x 10
-28
g/electron • γ •
Ф • v = 2.2 x 10
-3
dynes.
If the ion wind was made up of aluminum ions instead of electrons, the resulting force would be only thirty-eight-fold greater.
By comparison, the lifting force Brown observed amounted to 110 gm • 980 cm/sec
2
= 1.08 x 10
5
dynes.
This vertical-lift device performed much better than the tethered electrokinetic discs that Brown flew in his demonstration for Will Cady, the scientist from the ONR.
It developed fourteen times greater thrust when electrified at a voltage that was more than five times higher.
Also, it consumed thirty times less power when operated under vacuum conditions.
Moreover, Brown’s apparatus would have yielded a far greater thrust if it had used barium titanate for its dielectric instead of Pyrex.
Barium titanate ceramics can have a dielectric constant, K, of around 5,000 when charged with a DC potential, but when rapidly charged and discharged at frequencies of hundreds of megahertz, its K value may drop to about 50.
The lower value may be the more relevant here because, as discussed in section 3.4 of this chapter, it appears that he was cyclically varying the voltage potential across the plates of his electrokinetic apparatus at frequencies of around 750 megahertz to maintain a high thrust condition.
The “Electrohydrodynamics” report notes that thrust on the electrokinetic apparatus was observed to increase directly with the K value of the dielectric and according to the square (or in some cases the cube) of the applied voltage.
Consequently, a dielectric having a K equal to 50, which is about twelve times greater than the dielectric constant for Pyrex, would produce a twelvefold-greater thrust.
Also considering that barium titanate has a mass density 2.7 times that of Pyrex, it should develop a proportionately greater thrust when subject to a gravitational gradient.
So, one might expect overall a thirty-two-fold improvement, allowing Brown’s apparatus to generate a phenomenally high levitating force of about 3.5 kilograms!
If this high-K dielectric device consumed only half a watt of power, its thrust-to-power ratio would have had the unusually high value of 70,000 newtons per kilowatt, almost five thousand times that of a jet engine.
The measurements reporting a power consumption of only half a watt may have been referring to just the DC power consumption.
If substantially greater power was needed to establish an AC field across the apparatus, then the thrust-to-power ratio value estimated above would have to be reduced accordingly.
If tests were conducted with barium titanate, curiously, they are not mentioned in the report.
Brown probably did not openly discuss such test results because they were so phenomenal.
If reports were written, it is possible that they are currently classified.
Consider the usefulness of this technology for spaceflight.
Suppose that a high-K electrokinetic thruster was able to achieve a thrust-to-power ratio of 70,000 newtons per kilowatt.
Energized by a 3-kilowatt power source, a bank of 6,000 asymmetrical capacitors could develop a thrust of 21 metric tons (210,000 newtons), enough to propel a small, 100-ton spacecraft to Mars in just over five days.
Using chemical or nuclear rocket propulsion, the same trip would require anywhere from five to seven months and demand a far greater fuel load.
If this 100-ton spacecraft were placed in space and left to accelerate under the influence of this 0.21-g force (21 tons/100 tons), its propulsion efficiency would increase linearly with time.
By the end of one second, when it had attained a velocity of about 2 meters per second, its propulsion efficiency would already have reached 7,000 percent.
*7
Moreover, its efficiency would continue to increase tenfold with every additional tenfold increase in flight time.
Because kinetic energy far in excess of the inputted electric energy appears to be created out of nowhere, Brown’s device, by its nature, violates the first law of thermodynamics.
Such iconoclastic results become the new norm when one steps into the era of field propulsion.
3.3 • NONLINEAR FIELDS
Unlike his tethered flying disc models, Brown’s levitating saucer models had no bumper wires for generating positive and negative ions.
An idea of how they achieved their high antigravity thrust was put forth in Brown’s “electrokinetic apparatus” patent, filed in 1958 and awarded in 1965, which discussed the assembly shown in figure 3.6.
The patent attributes the thrust of the device to its ability to produce a nonlinear field gradient between its positive and negative electrodes, the gradient being steeper at the negative electrode than at the positive electrode.
This was accomplished by curving the upper, positively charged surface into the form of a parabaloid and by reducing the size of the negative electrode.
The negative electrode was pictured either as a small-diameter sphere or as a disc placed at the positive electrode’s geometrical focus.
Regarding the importance of having a nonlinear field gradient across the dielectric member, Brown wrote:
I have discovered that if two electrodes are mounted on opposite ends of a dielectric member, and a field emanates from these electrodes which produces a linear gradient through the dielectric member as shown by dotted line 30 of FIGURE 3 [dashed line in figure 3.6], then no thrust is produced by the dielectric member.
However, if the field is distorted to produce a nonlinear gradient such as graphically represented by line 32 in FIGURE 3 [solid line in figure 3.6], then a thrust will be produced which thrust will be related to the degree of nonlinearity of the field gradient.
One way to produce a gradient which varies nonlinearly is to shape one of the electrodes in a form of an arcuate surface .
.
.
17
Brown’s patent suggests that the electric field gradient could also be made nonlinear by using a conical dielectric member that tapers toward the negative electrode or one whose dielectric constant K progressively changes along its length, that is, one that preferably decreases toward the negative electrode.
It also points out that the force is directed from a region where the electric flux density is high toward a region where the electric flux density is low.
For example, it states:
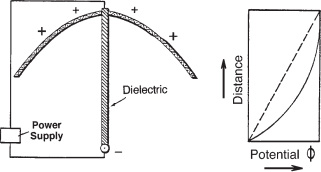
Figure 3.6.
An electrogravitic thrust-producing device described in Brown’s 1965 patent (left), electric potential,
Ф, plotted versus distance along the length of the dielectric rod (right).
By attaching a pair of electrodes to opposite ends of a dielectric member and connecting a source of high electrostatic potential to these electrodes, a force is produced in the direction of one electrode provided that electrode is of such configuration to cause the lines-of-force to converge steeply upon the other electrode.
The force, therefore, is in a direction from the region of high flux density toward the region of low flux density, generally in the direction through the axis of the electrodes.
The thrust produced by such a device is present if the electrostatic field gradient between the two electrodes is nonlinear.
This nonlinearity of gradient may result from a difference in the configuration of the electrodes, .
.
.
from the shape of the dielectric member, from a gradient in the density, electric conductivity, electric permittivity and magnetic permeability of the dielectric member, or a combination of these factors.
18
Brown often emphasized that nonlinear electric fields were central to the phenomenon.
In a letter to Turman in 1968, he wrote that this 1965 patent held the key to understanding electrogravitics:
*8
The Patent No.
3,187,206 contains the essential teaching in electrogravitics.
A definition of the electrogravitic force might be “the ponderomotive force developed within a high-K dielectric under electrical strain.”
The patent teaches the use of nonlinear electric fields such as those internally developed in truncated cones of dielectric material.
.
.
.
The belief that the phenomenon is gravitic in nature is based almost entirely upon the appearance of the effects of mass (in the dielectric material) on the force exhibited.
19
Brown did not elaborate as to why a nonlinear electric field would produce increased thrust.
He arrived at his conclusions from careful observation but offered no theory to account for them.
However, by extending the theory described in chapter 1 for the electrogravitic effects of charge densities, it should be possible to gain an understanding of how nonlinear electric fields might boost a capacitor’s electrogravitic thrust.
This involves understanding how a nonlinear field would produce a
virtual-charge-density gradient
across a dielectric and how this gradient, in turn, would generate a gravity field gradient.
A virtual charge is a charge source, like an electron or proton, but is one that is not associated with any particle.
It instead arises from the ambient electric field continuum whenever that field varies with distance in a nonlinear manner.
This virtual-charge concept is most easily understood within the “ether physics” context presented in the next chapter.
Thus we will defer discussing the virtual-charge electrogravitic thrust effects on Brown’s electrokinetic apparatus until after the subquantum kinetics ether concept has been introduced.
It should be noted here, however, that with sufficient field nonlinearity, the electrogravitic thrust effects produced by virtual charges could far exceed those produced by the real charges being applied to the capacitor plates.
Part of the thrust developed by Brown’s electrokinetic apparatus would also have been produced by unbalanced
electrostatic
forces acting on the charges on the capacitor’s plates.
An unbalanced residual force would have been present because the capacitor’s nonlinear electric field would have exerted more force on the smaller electrode than on the larger electrode.
Such a residual force would be absent in a conventional capacitor having equal-size electrodes.
Such capacitors establish a linear electric field across their dielectric when charged, the electric potential gradient being the same at their negative pole as at their positive pole.
The electric field gradient being created across the charged capacitor, then, would electrostatically attract the capacitor’s negatively charged electrode toward the field’s positive pole and the capacitor’s positively charged electrode toward the field’s negative pole.
Because both capacitor plates would carry the same surface charge density and be subject to the same field gradient, these two attractive forces would be equal to and opposite one another.
Hence, the capacitor would experience a compressive force pushing the plates in toward the dielectric.
However, since these forces would balance one another, the capacitor as a whole would experience no net translatory motion.
In this force analysis, we assume that the capacitor’s electric field is anchored neither to the capacitor’s charges nor to the capacitor’s plates, but rather resides in the capacitor’s environs as an independent entity capable of exerting forces on the very same charges that created it.
Now, let us instead consider an asymmetrical capacitor of the kind that Brown used in his electrokinetic saucer experiments, one whose positive electrode is larger than its negative electrode (figure 3.7).
The electric field across this type of capacitor varies with distance in a nonlinear fashion, the electric flux density and field gradient being highest at the capacitor’s negative pole and lowest at its positive pole.
Suppose the capacitor is in a vacuum and, hence, has no ionic charges around it.
The electric field established in the vicinity of the lower negative electrode would induce an attractive force on the negative charges gathered there, which would be directed upward toward the electric field’s positive pole.
Also, the electric field established in the vicinity of the upper positive electrode end of the dielectric would induce an attractive force on the positive charges gathered there, which would be directed downward toward the field’s negative pole (figure 3.7).
However, since the electric field lines converge toward the negative electrode, the field gradient would be stronger there as compared with the positively charged end of the dielectric.
Consequently, the force pulling the lower end of the dielectric upward would be greater than the force pulling the upper end of the dielectric downward.
As a result, the capacitor as a whole would experience a net force directed upward toward its larger electrode.
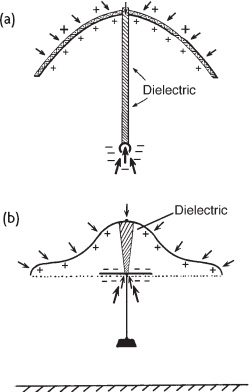
Figure 3.7.
Unbalanced electrostatic repulsion forces induced on the dielectric members of two of Brown’s saucer designs: (a) design illustrated in his electrokinetic apparatus patent and (b) apparatus used in test witnessed by Kitselman.
(P.
LaViolette, © 2007)
Moreover, the force vectors on the upper electrode would have only a fraction of their total force directed downward.
The more peripheral regions of the positive electrode that make up most of the electrode’s surface would have their force vectors angled inward, toward the dielectric axis, with a lesser vector component being directed downward (see figure 3.7).
It then becomes clear why Brown fashioned his upper electrode into an umbrella-like arcuate shape, so that it curved downward to enclose all or most of the dielectric column.
This pulled a greater number of positive charges toward the electrode’s periphery and changed the direction of the attractive forces affecting those upper electrode charges, causing their vectors to be angled more horizontally, perpendicular to the dielectric axis.
Thus the downward force on the upper electrode would be less than the upward force on the lower electrode both because the upper electrode force magnitudes would be less and because they would be vectored so that only a portion of their thrust would be aimed downward.
Such unbalanced electrostatic forces would produce a thrust toward the larger electrode even if the capacitor’s polarity was reversed.
This is because the direction of the residual electrostatic force is not linked to plate polarity, but to the direction in which the electric field diverges.
The directional dependence for this electrostatic thrust differs from that for the electrogravitic thrust which, as explained in the previous section, is always directed toward the positive electrode.
So, depending on the polarity of the DC field across the asymmetrical capacitor, the unbalanced electrostatic thrust would either reinforce or oppose the electrogravitic thrust.
In his patent, Brown mentions that his asymmetrical electrokinetic apparatus always produces a thrust toward its larger electrode, even when the electrode polarity is reversed, although he mentions that the thrust is greater when the larger electrode is positive rather than negative.
This suggests that the electrogravitic force is being overpowered by the unbalanced electrostatic thrust that depends on field geometry rather than plate polarity.
However, his statements here appear to be referring to the case where his thruster is energized with a DC potential.
He does not comment on the correlation of thrust direction with plate polarity when an AC field is energizing the apparatus.
In responding to the unbalanced electrostatic force, the upward movement of Brown’s electrokinetic apparatus would occur
with no recoil displacement of the electric field it was generating
.
In fact, as the apparatus moves upward, the charges that generate this field would also move upward, so the field would move upward as well.
Thus, by means of this unbalanced force effect, Brown’s saucer, so to speak, “picks itself up by its own bootstraps.”
