The Dancing Wu Li Masters (15 page)
Read The Dancing Wu Li Masters Online
Authors: Gary Zukav

It was disconcerting enough when light, which is made of waves, began to behave like particles, but when electrons, which
are
particles, began to behave like waves, the plot became unbearably thick.
The unfolding of quantum mechanics was (and still is) a drama of high suspense. Werner Heisenberg wrote:
I remember discussions with Bohr [in 1927] which went through many hours till very late at night and ended almost in despair; and when at the end of the discussion I went alone for a walk in the neighboring park I repeated to myself again and again the question: Can nature possibly be as absurd as it seemed to us in these atomic experiments.
2
Subsequent experiments were to reveal that not only subatomic particles, but atoms and molecules as well have associated matter waves. The title of Donald Hughes’s pioneer book,
Neutron Optics
, provides eloquent testimony of the merger between waves and particles to which Prince de Broglie’s doctoral thesis gave birth. Theoretically, in fact,
everything
has a wavelength—baseballs, automobiles, and even people—although their wavelengths are so small that they are not noticeable.
De Broglie himself was not very helpful in explaining his theory. It predicted what the Davisson-Germer experiment proved: that matter, like electrons, has a wave-like aspect. His equation even foretold the wavelength of these waves. Nonetheless, no one knew what these waves actually were (no one does yet). De Broglie called them waves which “correspond” to matter, but he did not explain what “correspond” meant.
Is it possible for a physicist to predict something, calculate equations which describe it, and still not know what he is talking about?
Yes. As Bertrand Russell put it:
Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true.
3
This is why the physicists at Copenhagen decided to accept quantum mechanics as a complete theory even though it gives no explana
tion of what the world is “really like,” and even though it predicts probabilities and not actual events. They accepted quantum mechanics as a complete theory because quantum mechanics correctly correlates experience. Quantum mechanics, and, according to the pragmatists, all science, is the study of correlations between experiences. De Broglie’s equation correctly correlates experiences.
De Broglie merged the wave-particle paradox which came to light (hissss) through the genius of Thomas Young (double-slit experiment) and Albert Einstein (photon theory). In other words, he connected the two most revolutionary phenomena of physics, the quantum nature of energy and the wave-particle duality.
De Broglie presented his matter-wave theory in 1924. During the next three years quantum mechanics crystallized into what it essentially is today. The world of Newtonian physics, simple mental pictures, and common sense disappeared. A new physics took form with an originality and force that left the mind reeling.
After de Broglie’s matter waves came the Schrödinger wave equation.
De Broglie’s matter waves seemed to Erwin Schrödinger, the Viennese physicist, a much more natural way of looking at atomic phenomena than Bohr’s planetary model of the atom. Bohr’s model of hard, spherical electrons revolving around a nucleus at specific levels and emitting photons by jumping from one level to another explained the color spectrum of simple atoms, but it said nothing about why each shell contains only a certain number of electrons, no more and no less. It also did not explain
how
the electrons do their jumping (for example, what is happening to them between shells).
*
Stimulated by de Broglie’s discovery, Schrödinger hypothesized that electrons are not spherical objects, but
patterns of standing waves
.
Standing waves are familiar phenomena to anyone who has
played with a clothesline. Suppose that we tie one end of a rope to a pole, and then pull it tight. On this rope there are no waves at all, either standing or traveling. Now suppose that we flick our wrist sharply downward and then upward. A hump appears in the rope and travels down the rope to the pole where it turns upside down and returns to our hand. This traveling hump (figure A) is a traveling wave. By sending a series of humps down the rope, we can set up the patterns of standing waves shown below, and more that are not shown.
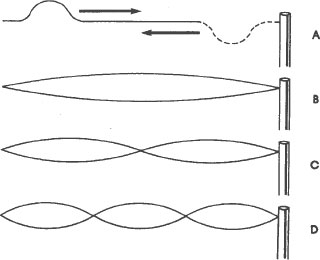
The simplest of these is the pattern shown in figure B. This pattern is formed by the superposition of two traveling waves, a direct one and a reflected one traveling in the opposite direction. It is the pattern, not the rope, which does not move. The widest point in the standing wave remains “stationary,” and so do the points at the ends of the standing wave. These points are called nodes. There are two of them in the simplest standing pattern, one at our hand and one at the
pole where the rope is attached. These stationary patterns, superpositions of traveling waves, are called standing waves.
No matter how long or short our rope is, there can be only a whole number of standing waves on it. That is, it can have a pattern of one standing wave, or a pattern of two standing waves, or a pattern of three, four, five, and so on, standing waves but it can never have a pattern of one and one half standing waves, or a pattern of two and one fourth standing waves. The standing waves must divide the rope evenly into whole sections. Another way to say this is that we can increase or decrease the number of standing waves on a rope only by a whole number of them. This means that the only way that the number of standing waves on a rope can increase or decrease is
discontinuously
(that word, again!).
Furthermore, standing waves on a rope cannot be just any size. They always will be restricted to those lengths which divide the rope evenly. The actual size of the waves depends upon how long the rope is, but no matter what length the rope, there will be only certain lengths which divide it evenly.
All of this was old stuff in 1925. Plucking a guitar string establishes patterns of standing waves on it. Blowing air into an organ pipe creates standing wave patterns in it. What was new was Schrödinger’s realization that
standing waves are “quantized” the same way that atomic phenomena are!
In fact, Schrödinger proposed that electrons
are
standing waves.
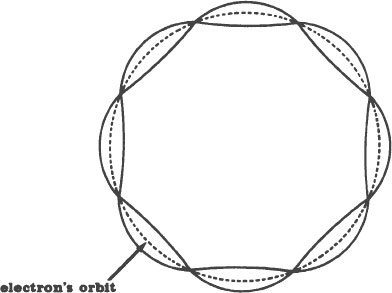
In retrospect, this is not as fantastic as it first sounds. At the time, however, it was a stroke of genius. Picture an electron in orbit around a nucleus. Each time the electron completes a journey around the nucleus, it travels a certain distance. That distance is a certain length, like our rope was a certain length. Similarly, only a whole number of standing waves, never a fraction of one, can form in this length. (Length of what is an unanswered question.)
Schrödinger proposed that each of these standing waves is an electron! In other words, he proposed that electrons are the segments of vibrations bounded by the nodes. A drawing of this is on the next page.
So far, we have talked about standing waves on a line, like a clothesline or a guitar string, but standing waves also occur in other
mediums, like water. Suppose that we throw a rock into a round pool. Waves radiate from its point of entry. These waves are reflected, sometimes more than once, off different sides of the pool. When the reflected traveling waves interfere with each other they create a complex pattern of standing waves which is our old friend, interference.
Where the crest of one wave meets the trough of another wave, they cancel each other and the surface of the water along this line of interaction is calm. These calm areas are the nodes which separate the standing waves. In the double-slit experiment, the nodes are the dark bands in the pattern of alternating light and dark areas. The light bands are the crests of the standing waves.
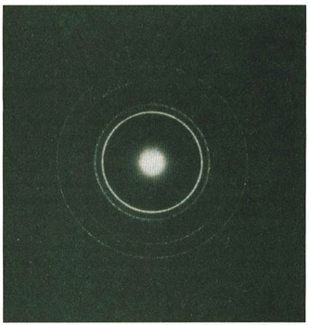
Schrödinger chose the model of a small tub of water with its complex and intricate interference pattern to explain the nature of the
atom. This model is, as he put it, an “analogue” of electron waves in an atom-sized basin.
The ingenious but nevertheless somewhat artificial assumptions of [Bohr’s model of the atom]…are replaced by a much more natural assumption in de Broglie’s wave phenomena. The wave phenomenon forms the real “body” of the atom. It replaces the individual punctiform [pointlike] electrons, which in Bohr’s model swarm around the nucleus.
4
Standing waves on clotheslines have two dimensions: length and width. Standing waves in mediums like water, or on the head of a conga drum, have three dimensions: length, width, and depth. Schrödinger analyzed the standing wave patterns of the simplest atom, hydrogen, which has only one electron. In hydrogen alone he calculated, using his new wave equation, a multitude of different possible shapes of standing waves. All of the standing waves on a rope are identical. This is not true of the standing waves in an atom. All of them are three-dimensional and all of them are different. Some of them look like concentric circles. Some of them look like butterflies, and others look like mandalas, as in the illustration on the next page.
Shortly before Schrödinger’s discovery, another Austrian physicist, Wolfgang Pauli, discovered that no two electrons in an atom can be exactly alike. The presence of an electron with one particular set of properties (“quantum numbers”) excludes the presence of another electron with exactly the same properties (quantum numbers) within the same atom. For this reason, Pauli’s discovery became known as the Pauli exclusion principle. In terms of Schrödinger’s standing wave theory, Pauli’s exclusion principle means that once a particular wave pattern forms in an atom, it excludes all others of its kind.
Schrödinger’s equation, modified by Pauli’s discovery, shows that there are only two possible wave patterns in the lowest of Bohr’s energy levels, or shells. Therefore, there can be only two electrons in it. There are eight different standing-wave patterns possible in the next energy level, therefore there can be only eight electrons in it, and so on.
*
,
†

From
Modern College Physics
, Harvey White, N.Y., Van Nostrand, 1972.
