The Dancing Wu Li Masters (40 page)
Read The Dancing Wu Li Masters Online
Authors: Gary Zukav

Now let us return to the distributive law: “A, and B or C” equals “A and B, or A and C.” (The whole purpose of making a transition table was to make a lattice to use in disproving the distributive law.)
Mathematicians use lattice diagrams to determine which elements in the lattice are connected and in what way.
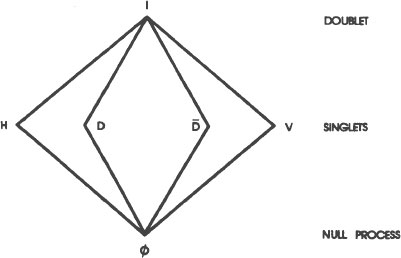
For example, to see how two elements in the lattice are connected by the word “and,” follow the lines leading from the elements in ques
tion
down
to a point where they both meet (which mathematicians call the “greatest lower bound”). If we are interested in “H and D,” we follow the lines
downward
from H and from D and find that they meet at ø. Therefore, the lattice tells us that “H and D” equals “ø.” If we are interested in “I and H,” we follow the line
downward
from the highest starting point on the lattice (I) and find that the lowest common point of I and H is H. Therefore, the lattice tells us that “I and H” equals “H.”
To see how two elements in the lattice are connected by the word “or,” follow the lines leading from the elements in question
up
to a point where they both meet (which mathematicians call the “least upper bound”). For example, if we are interested in “H or V,” we follow the lines
upward
from H and from V and find that they meet at I. Therefore, the lattice tells us that “H or V” equals “I.” Similarly, to find “D or I,” we follow the lines
upward
to their highest common point, which is I. Therefore, the lattice tells us that “D or I” equals “I.”
The rule is simple: “and” goes
down
, “or” goes
up
.
Go
down
the lattice to find “and,” go
up
the lattice to find “or.”
Now we come to the proof itself. The proof itself is considerably simpler than the preliminary explanations. The distributive law says that “A, and B or C” equals “A and B, or A and C.” To see whether this is true of experience or not we simply insert some of our actual states of polarization into the formula and solve it using the lattice method. For example, the distributive law says that “Horizontally polarized light and vertically polarized light or diagonally polarized light” equals “Horizontally polarized light and vertically polarized light, or horizontally polarized light and diagonally polarized light.” Using the abbreviations that we already have used, this is written: “H, and D or V” equals “H and D, or H and V.”
Returning to the lattice, let us examine the left side of this statement first. Solving for “D or V,” we follow the lines on the lattice upward from D and from V to their highest common point (“or” goes
up
). They meet at I. Therefore, the lattice tells us that “D or V” equals “I.” Substituting “I” for the original “D or V,” we have left
on this side of the statement “H and I.” Following the lines from H and from I downward on the lattice (“and” goes
down
), we find that their lowest common point is at H. Therefore, the lattice tells us that “H and I” equals “H.”
In short:
“H, and D or V” equals “H and D, or H and V”
“H and I” equals “H and D, or H and V”
“H” equals “H and D, or H and V”
We solve the right side of this statement in the same way. Solving for “H and D,” we follow the lines on the lattice downward from H and from D to their lowest common point. They meet at ø. Therefore, the lattice tells us that “H and D” equals “ø.”
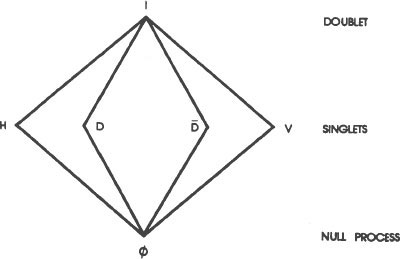
Substituting “ø” for “H and D,” we are left with “ø, or H and V” on the right side of the statement. To solve for “H and V,” we follow the lines on the lattice downward from H and from V to their lowest common point. They also intersect at ø. Therefore, the lattice tells us that “H and V” equals “ø.” Substituting “ø” for “H and V”
we now are left with “ø or ø” on the right side of the original statement. Both the lattice and common sense tell us that “ø or ø” equals “ø.”
In short:
“H” equals “H and D, or H and V”
“H” equals “ø, or H and V”
“H” equals “ø or ø”
“H” equals “ø”
But “H” does
not
equal “ø!” “H” is horizontally polarized light and “ø” is a non-experiment—a lack of any emission at all. The distributive law does not work!
Here is Birkhoff and von Neumann’s proof again. It is important because, simple as it is, it could end an illusion millennia old: the illusion that symbols and experience follow the same set of rules. Except for the mathematical symbols that represent the connectives “and” and “or,” this is exactly the way that physicists read it:
“H, and D or V” “H and D, or H and V”
“H and D, or H and V”
“H and I” “ø, or H and V”
“ø, or H and V”
“H”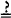 “ø or ø”
“ø or ø”
“H” ≠ “ø”
Finkelstein’s theory is a theory of
process
. Quantum logic is only one part of it. According to this theory, the basic unit of the universe is an event, or a process. These events link in certain ways (allowed transitions) to form webs. The webs in turn join to form larger webs. Farther up the ladder of organization are coherent superpositions of different webs (things which are neither “this web” nor “that web” but distinct entities in themselves).
The basic events of Finkelstein’s theory do not exist in space and time. They are
prior
to space and time. According to Finkelstein,
space, time, mass, and energy are secondary qualities
which are derived
from the basic events of the universe. In fact, Finkelstein’s latest paper is called “Beneath Time.”
This bold theory is a radical departure from conventional physics and from conventional thought. The mathematics of Finkelstein’s theory, which is called quantum topology, is remarkably simple compared to the complex mathematics of quantum theory and relativity. Quantum topology is as yet incomplete (lacking “proof”). Like many theories, it may never be complete. Unlike most other theories, however, it contains the potential to alter radically our conceptual framework.
Von Neumann’s discovery that our thought processes (the realm of symbols) project illusory restrictions onto the real word is essentially the same discovery that led Einstein to the general theory of relativity. Einstein disproved the universality of Euclidean geometry. Until the general theory of relativity, Euclidean geometry had been accepted without question as the underlying structure of the universe. Birkhoff and von Neumann disproved the universality of classical logic. Until now, classical logic has been accepted without question as a natural reflection of the nature of reality.
A powerful awareness lies dormant in these discoveries: an awareness of the hitherto-unsuspected powers of the mind to mold “reality,” rather than the other way round. In this sense, the philosophy of physics is becoming indistinguishable from the philosophy of Buddhism, which is the philosophy of enlightenment.
A vital aspect of the enlightened state is the experience of an all-pervading
unity. “This” and “that” no longer are separate entities. They are different
forms
of the same thing. Everything is a
manifestation
. It is not possible to answer the question, “Manifestation of
what?
” because the “what” is that which is beyond words, beyond concept, beyond form, beyond even space and time. Everything is a manifestation of that which is. That which is, is. Beyond these words lies the experience; the experience of that which is.
The forms through which that which is manifests itself are each and every one of them perfect.
We
are manifestations of that which is.
Everything
is a manifestation of that which is. Everything and everybody is exactly and perfectly what it is.
A fourteenth-century Tibetan Buddhist, Longchenpa, wrote:
Since everything is but an apparition
Perfect in being what it is,
Having nothing to do with good or bad,
Acceptance or rejection,
One may well burst out in laughter.
1
We might say, “God’s in His heaven and all’s well with the world,” except that according to the enlightened view, the world couldn’t be any other way. It is neither well nor not well. It simply is what it is. What it is is perfectly what it is. It couldn’t be anything else. It is perfect. I am perfect. I am exactly and perfectly who I am. You are perfect. You are exactly and perfectly who you are.
If you are a happy person, then that is what you perfectly are—a happy person. If you are an unhappy person, then
that
is what you perfect are—an unhappy person. If you are a person who is changing, then
that
is what you perfectly are—a person who is changing. That which is is that which is. That which is not is that which is. There is nothing which is not that which is. There is nothing other than that which is. Everything is that which is. We are a part of that which is. In fact,
we are that which is
.
If we substitute “subatomic particles” for people in this scheme, we have a good approximation of the conceptual dynamics of particle physics. Yet, there is another sense in which this aspect of unity has entered physics. The pioneers of quantum physics noticed a strange “connectedness” among quantum phenomena. Until recently this oddity lacked any theoretical significance. It was regarded as an accidental feature which would be explained as the theory developed.
In 1964, J. S. Bell, a physicist at the European Organization for Nuclear Research (CERN) in Switzerland, zeroed in on this strange connectedness in a manner that may make it the central focus of physics in the future. Dr. Bell published a mathematical proof which came to be known as Bell’s theorem. Bell’s theorem was reworked and refined over the following ten years until it emerged in its present form. Its present form is dramatic, to say the least.
Bell’s theorem is a mathematical construct which, as such, is indecipherable to the nonmathematician. Its implications, however, could affect profoundly our basic world view. Some physicists are convinced that it is the most important single work, perhaps, in the history of physics. One of the implications of Bell’s theorem is that, at a
deep and fundamental level, the “separate parts” of the universe are connected in an intimate and immediate way.
In short, Bell’s theorem and the enlightened experience of unity are very compatible.
The unexplained connectedness of quantum phenomena shows itself in several ways. The first way we already have discussed. It is the double-slit experiment. When both slits in a double-slit experiment are open, the light waves going through them interfere with each other to form a pattern of alternating light and dark bands on a screen. When only one slit in a double-slit experiment is open, the light waves going through it illuminate the screen in the ordinary way. How does a single photon in a double-slit experiment know whether or not it can go to an area on the screen that must be dark if both slits are open?
The great multitude of photons of which a single photon eventually will be a part distributes itself in one way if one slit is open, and in an entirely different way if both slits are open. The question is, assuming that a single photon goes through one of the two slits,
how does it know whether or not the other slit is open?
Somehow it does. An interference pattern
always
forms when we open both slits, and it
never
forms when we close one of the slits.
However, there is another experiment in which this apparent connectedness of quantum phenomena is even more perplexing. Suppose that we have what physicists call a two-particle system of zero spin. This means that the spin of each of the particles in the system cancels the other. If one of the particles in such a system has a spin
up
, the other particle has a spin
down
. If the first particle has a spin
right
, the second particle has a spin
left
. No matter how the particles are oriented, their spins are always equal and opposite.
Now suppose that we separate these two particles in some way that does not affect their spin (like electrically). One particle goes off in one direction and the other particle goes off in the opposite direction.
The spin of a subatomic particle can be oriented by a magnetic field. For example, if a beam of electrons with randomly oriented spin is sent through a particular type of magnetic field (called a Stern-Gerlach device), the magnetic field splits the beam into two equal smaller beams. In one of them all of the electrons have a spin
up
and in the other all of the electrons have a spin
down
. If only one electron goes through this magnetic field, it will come out of it with either a
spin
up
or a spin
down
. (We can design the experiment so that the odds are 50–50) (first drawing, previous page).
If we reorientate the magnetic field (change its axis) we can give all of the electrons a spin
right
or a spin
left
instead of a spin up or a spin down. If only one electron goes through the magnetic field when it is oriented this way, it will come out of it with either a spin
right
or a spin
left
(equal chance either way) (second drawing, previous page).
Now suppose that after we separate our original two-particle system we send one of the particles through a magnetic field that will give it either a spin
up
or a spin
down
. In this case, let us say that the particle comes out of the magnetic field with a spin
up
. This means that we automatically know that the other particle has a spin
down
. We do not have to make a measurement on the other particle because we know that its spin is equal to and opposite to that of its twin.
The experiment looks like this:
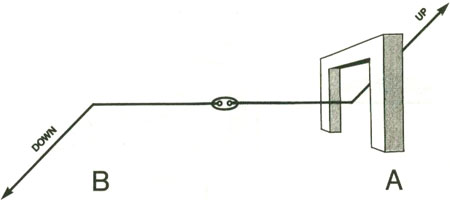
The original two-particle system with zero spin is at the center. One of the particles goes to area A. In area A it goes through a Stern-Gerlach device. In this case, the Stern-Gerlach device gives it a spin
up
. Therefore, we know
without measuring
that the other particle, which has gone to area B, has a spin
down
.
Albert Einstein, Boris Podolsky, and Nathan Rosen thought up this experience over forty-five years ago. Actually, this version of the Einstein-Podolsky-Rosen experiment (using spin states) was thought up by David Bohm, a physicist at the University of London. This ver
sion usually is used to illustrate the Einstein-Podolsky-Rosen effect. (The original paper dealt with positions and momenta.)
In 1935, Einstein, Podolsky, and Rosen published their thought experiment in a paper entitled, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?”
2
At that time, Bohr, Heisenberg, and the proponents of the Copenhagen Interpretation of Quantum Mechanics were saying that quantum theory is a complete theory even though it doesn’t provide any picture of the world separate from our observations of it. (They’re still saying it.) The message that Einstein, Podolsky, and Rosen wanted to convey to their colleagues was that the quantum theory is
not
a “complete” theory because it does not describe certain important aspects of reality which are physically real even if they are not observed. The message that their colleagues got, however, was quite different. The message that their colleagues got was that the particles in the Einstein-Podolsky-Rosen thought experiment somehow are connected in a way that transcends our usual ideas about causality.
For example, if the axis of the Stern-Gerlach device in our hypothetical experiment were changed to make the particles spin
right
or
left
instead of
up
or
down
, the experiment would look like this:

The particle in area A would have a spin
right
instead of a spin
up
. This means that the particle in area B would have a spin
left
instead of a spin
down
. Its spin is always equal and opposite that of its twin.
Now suppose that the axis of the Stern-Gerlach device is changed while the particles are
in flight
. Somehow the particle traveling in area B
“knows” that its twin in area A is spinning
right
instead of
up
and so it spins
left
instead of
down
. In other words,
what we did in area A (changed the axis of the magnetic field) affected what happened in area B
. This strange phenomenon is known as the Einstein-Podolsky-Rosen (EPR) effect.
Einstein, Podolsky, and Rosen’s thought experiment is the Pandora’s Box of modern physics. It inadvertently illustrated an unexplainable connectedness between particles in two different places. The particle in area B seems to know
instantaneously
the spin status of the particle in area A.
*
This connectedness allows an experimenter in one place (area A) to affect the state of a system in another place (area B).
“It is rather discomforting,” remarked Erwin Schrödinger, in reference to this phenomenon,
that the [quantum] theory should allow a system to be steered or piloted into one or the other type of state at the experimenter’s mercy in spite of his having no access to it.
3
At once physicists realized that this peculiar situation raises a critical question: “How can two of anything communicate so quickly?”
According to the usual ideas in physics, information is carried from one place to another by a signal. Without a carrier there is no communication. For example, the most common form of communication is talking. The information that we convey by talking is carried (in a face-to-face conversation) by sound waves. Sound waves only travel so fast (about 700 miles per hour). Therefore, how long it takes my information to get from me to you depends upon how far away from me you are. The fastest communication signal is an electromagnetic wave, like a light wave or a radio wave. These travel at approxi
mately 186,000 miles per second. Almost all of physics rests upon the assumption that
nothing in the universe can travel faster than the speed of light
.
*
The extraordinarily high velocity of light makes communication by light signal
seem
instantaneous. I seem to see you nod your head at the moment that you actually do it. Nonetheless, communication by light signal is not instantaneous. How long it takes my information to travel via light signal from me to you depends upon how far away from me you are. In most instances, the travel time required is so brief that it scarcely can be measured. It takes several seconds, however, for a radio signal to travel from the earth to the moon and back.
