The Essential Galileo (56 page)


This proposition having been demonstrated, let us next consider the case of prisms and cylinders that are similar. Concerning these we shall show
Proposition 6
:
In the case of similar cylinders and prisms, the compound moments, namely, those produced by their own weight and length (which latter acts as a lever arm), bear to each other a ratio that is the three-halves power of the ratio between the resistances of their bases.
In order to prove this, let us consider the two similar cylinders
AB
and
CD.
Then I say that the moment of the cylinder
AB
, opposing the resistance of its base
B
, bears to the moment of
CD
, opposing the resistance of its base
D
, a [164] ratio that is the three-halves power of the ratio between the resistance of the base
B
and the resistance of the base
D.
For, the solids
AB
and
CD
are effective in opposing the resistances of their bases
B
and
D
in proportion to both their weights and the mechanical advantages of their lever arms; and the advantage of the lever arm
AB
is equal to the advantage of the lever arm
CD
(this is true because, in virtue of the similarity of the cylinders, the length
AB
is to the radius of the base
B
as the length
CD
is to the radius of the base
D
); so it follows that the total moment of the cylinder
AB
is to the total moment of the cylinder
CD
as the weight alone of the cylinder
AB
is to the weight alone of the cylinder
CD
, that is, as the volume of the cylinder
AB
is to the volume
CD;
but these are as the cubes of the diameters of their bases
B
and
D;
and the resistances of the bases, being to each other as their areas, are to each other consequently as the squares of their diameters; therefore, the moments of the cylinders are to each other as the three-halves power of the resistances of their bases.

S
IMP.
   This proposition strikes me as both new and surprising. At first glance it is very different from anything which I myself should have guessed. For since these figures are similar in all other respects, I should have certainly thought that the moments and the resistances of these cylinders would have borne to each other the same ratio.
S
AGR.
   This is the proof of the proposition to which I referred, at the very beginning of our discussion, as one imperfectly understood by me.
S
ALV.
   For a while, Simplicio, I used to think, as you do, that the resistances of similar solids were similar. But a certain casual observation showed me that similar solids do not exhibit a strength that is proportional to their size, the larger ones being less fitted to undergo rough usage just as tall men are more apt than small children to be injured by a fall. [165] And as we remarked at the outset, a large beam or column falling from a given height will go to pieces when under the same circumstances a small scantling or small marble cylinder will not break. It was this observation that led me to the investigation of the fact which I am about to demonstrate to you: it is a very remarkable thing that, among the infinite variety of solids that are similar one to another, there are no two whose moments are related in the same ratio to their own resistances.
S
IMP.
   You remind me now of a passage in Aristotle's
Questions of Mechanics
14
in which he tries to explain why it is that a wooden beam becomes weaker and can be more easily bent as it grows longer, notwithstanding the fact that the shorter beam is thinner and the longer one thicker. And, if I remember correctly, he explains it in terms of the simple lever.
S
ALV.
   Very true. But, since this solution seemed to leave room for doubt, Monsignor di Guevara,
15
whose truly learned commentaries have greatly enriched and illuminated this work, indulges in additional clever speculations with the hope of thus overcoming all difficulties. Nevertheless, even he is confused as regards this particular point, namely, whether, when the length and thickness of these solid figures increase in the same ratio, their strength and resistance to fracture, as well as to bending, remain constant. After much thought upon this subject, I have reached the following results. First I shall show that (
Proposition 7
):
Among prisms or cylinders that are similar and have weight
,
there is one and only one which, under the stress of its own weight, lies just on the limit between breaking and not breaking, such that every larger one is unable to carry the load of its own weight and breaks, while every smaller one is able to withstand some additional force tending to break it.

Let
AB
be a prism, the longest possible that will just sustain its own weight, so that if it be lengthened the least bit it will break. Then, I say, this prism is unique among all similar prismsâinfinite in numberâ in occupying [166] that boundary line between breaking and not breaking; so that every larger one will break under its own weight, and every smaller one will not break but will be able to withstand some force in addition to its own weight. Let the prism
CE
be similar to, but larger than,
AB;
then, I say, it will not remain intact but will break under its own weight. Lay off the portion
CD
, equal in length to
AB
. Since the resistance of
CD
is to that of
A
B as the cube of the thickness of
CD
is to the cube of the thickness of
AB
, that is, as the prism
CE
is to the similar prism
AB
, it follows that the weight of
CE
is the utmost load which a prism of the length
CD
can sustain; but the length of
CE
is greater; therefore the prism
CE
will break. Now take another prism
FG
smaller than
AB
, and let
FH
equal
AB
. Then it can be shown in a similar manner that the resistance of
FG
is to that of
AB
as the prism
FG
is to the prism
AB
, provided the distance
AB
(that is,
FH
) is equal to the distance
FG;
but
AB
is greater than
FG;
therefore the moment of the prism
FG
applied at
G
is not sufficient to break the prism
FG.
S
AGR.
   The demonstration is short and clear; while the proposition which, at first glance, appeared improbable is now seen to be both true and inevitable. In order therefore to bring this prism into that limiting condition that separates breaking from not breaking, it would be necessary to change the ratio between thickness and length either by increasing the thickness or by diminishing the length. An investigation of this limiting state will, I believe, demand equal ingenuity.
S
ALV.
   Nay, even more; for the question is more difficult. This I know because I spent no small amount of time in its discovery which I now wish to share with you.
Proposition 8: Given a cylinder or prism of the greatest length consistent with its not breaking under its own weight, and given a greater length, to find the thickness of another cylinder or prism of this greater length that shall be the only and largest one capable of withstanding its own weight.
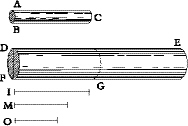
Let
BC
be the largest cylinder capable of sustaining its own weight; and let
DE
be a length greater than
AC.
The problem is to find the thickness of the [167] cylinder which, having the length
DE
, shall be the largest one just able to withstand its own weight. Let
I
be the third proportional to the lengths
DE
and
AC;
let the diameter
FD
be to the diameter
BA
as
DE
is to
I;
draw the cylinder
FE;
then, I say, among all cylinders having the same proportions, this is the largest and only one just capable of sustaining its own weight. Let
M
be the third proportional to
DE
and
I;
also let
O
be the fourth proportional to
DE, I
, and
M;
lay off
FG
equal to
AC
. Now since the diameter
FD
is to the diameter
AB
as the length
DE
is to
I
, and since
O
is the fourth proportional to
DE
,
I
, and
M
, it follows that the cube of
FD
is to the cube of
BA
as
DE
is to
O;
but the resistance of the cylinder
DG
is to the resistance of the cylinder
BC
as the cube of
FD
is to the cube of
BA;
hence the resistance of the cylinder
DG
is to that of cylinder
BC
as the length
DE
is to
O.
And since the moment of the cylinder
BC
is held in equilibrium by its resistance, we shall accomplish our end (which is to prove that the moment of the cylinder
FE
is equal to the resistance located at
FD
), if we show that the moment of the cylinder
FE
is to the moment of the cylinder
BC
as the resistance
DF
is to the resistance
BA
, that is, as the cube of
FD
is to the cube of
BA
, or as the length
DE
is to
O.
But the moment of the cylinder
FE
is to the moment of the cylinder
DG
as the square of
DE
is to the square of
AC
, that is, as the length
DE
is to
I;
and the moment of the cylinder
DG
is to the moment of the cylinder
BC
as the square of
DF
is to the square of
BA
, that is, as the square of
DE
is to the square of
I
, or as the square of
I
is to the square of
M
, or as
I
is to
O.
Therefore, by equidistance of ratios, it results that the moment of the cylinder
FE
is to the moment of the cylinder
BC
as the length
DE
is to
O
, that is, as the cube of
DF
is to the cube of
BA
, or as the resistance of the base
DF
is to the resistance of the base
BA.
This is what was being
sought.
