Warped Passages (32 page)

In 1927, the physicists Fritz London and Hermann Weyl demonstrated that the simplest quantum field theory description of forces involves internal symmetries similar to that in the spotlight example above. The connection between forces and symmetry is subtle, so you won’t usually read about it outside textbooks. Because you don’t really need to understand this connection to follow the discussion of the issues about masses—including the Higgs mechanism and the hierarchy problem of the next few chapters—you can skip ahead to the next chapter at this point if you want. But if you’re interested in the role of internal symmetry in the theory of forces and the Higgs mechanism, read on.
Symmetry and Forces
Electromagnetism, the weak force, and the strong force all involve internal symmetries. (Gravity is related to symmetries of space and time, and must therefore be considered separately.) Without internal symmetries, the quantum field theory of forces would be an intractable mess. To understand these symmetries, we need first to consider the
gauge boson polarizations
.
You might be familiar with the notion of polarization of light; for example, polarizing sunglasses reduce glare by letting through only light that is vertically polarized and eliminating the horizontally polarized light. In this case, polarizations are the independent directions in which the electromagnetic waves associated with light can oscillate.
Quantum mechanics associates a wave with every photon. Each individual photon has different possible polarizations as well, but not all imaginable polarizations are allowed. It turns out that when a photon travels in any particular direction, the wave can oscillate only in directions that are perpendicular to its direction of motion. This wave acts like water waves on the ocean, which also oscillate perpendicularly. That is why you see a buoy or a boat bob up and down as a water wave passes by.
The wave associated with a photon can oscillate in any direction perpendicular to its direction of motion (see Figure 57). Really, there is an infinite number of such directions: imagine a circle perpendicular to the line of motion, and you can see that the wave is able to oscillate in any radial direction (from the center to the outside of the circle), and there are an infinite number of such directions.
But in the physical description of these oscillations, we need only
two independent perpendicular oscillations to account for them all. In physics terminology they are called
transverse polarizations
. It is as if you had labeled a circle with
x
and
y
axes. No matter what line you draw from the center of the circle, it will always intersect the circle at a particular position—a particular pair of
x
and
y
values—and can therefore be uniquely specified by only two coordinates. Similarly (without going into the details of how this works), although there are an infinite number of directions that are perpendicular to the direction in which a wave travels, all of those directions can be obtained from combinations of polarized light in any two perpendicular directions.
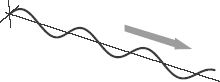
Figure 57.
A transverse wave oscillates perpendicularly to the direction of motion (in this case up and down, while the wave travels to the right).
The important thing is that, in principle, there could have been a third polarization direction, one that oscillates along the direction in which the wave travels (had it existed, it would have been called the
longitudinal
polarization).
15
That is how sound waves travel, for example. But no such polarization of the photon exists. Only two of the three conceivable independent polarization directions exist in nature. A photon never oscillates along its direction of motion or in the time direction: it oscillates only along the directions perpendicular to its motion.
Even if we didn’t already know from independent theoretical considerations that the longitudinal polarization was spurious, quantum field theory would have told us not to include it. If a physicist were to make calculations using a theory of forces that mistakenly included all three polarization directions, the theory’s predictions of their properties wouldn’t make sense. For example, she would predict ridiculously high gauge boson interactions rates. In fact, she would predict gauge bosons that interacted more often than always—that is, more than 100% of the time. Any theory that makes such nonsensical predictions is clearly wrong, and both nature and quantum field theory make it clear that this nonperpendicular polarization does not exist.
Unfortunately, the simplest theory of forces that physicists could formulate includes this spurious polarization direction. That is not so surprising because a theory that would work for any photon can’t possibly contain information about one particular photon traveling in one particular direction. And without such information, special
relativity would not distinguish any direction. In a theory that preserves the symmetries of special relativity (including rotational symmetry), you would need three directions—not two—to describe all the directions in which a photon could oscillate; in such a description, the photon could oscillate in any direction of space.
But we know that isn’t true. For any particular photon, its direction of motion is singled out and oscillation in that direction is forbidden. But you wouldn’t want to have to make a different theory for each and every photon, all with their own directions of travel. You would want a theory that works no matter which way a photon is travelling. Although you could try to make a theory that didn’t include the spurious polarization direction at all, it is far simpler and cleaner to respect rotational symmetry and eliminate the bad polarization in some other way. Physicists, aiming for simplicity, have recognized that quantum field theory works best when they include the spurious longitudinal polarization in their theory but add an extra ingredient to filter out the good, physically relevant predictions from the bad.
This is where internal symmetries enter the picture. The role of internal symmetries in the theory of forces is to eliminate the contradictions that the unwanted polarization would create without making us forfeit the symmetries of special relativity. Internal symmetries are the simplest way to filter out the polarization along the direction of travel that independent theoretical considerations and experimental observations tell us does not exist. They classify polarizations into good and bad categories, those that are consistent with the symmetries and those that are not. The way it works is a bit too technical to explain here, but I can give you the general idea by using an analogy.
Suppose you have a shirt-making machine that can make left and right sleeves in two sizes, short and long, but for some reason the inventor of the machine neglected to include a control to ensure that the left and right sleeves are the same size. Half the time you will make useful shirts—ones with two long sleeves or two short sleeves—but half the time you will make useless, unbalanced shirts with one short and one long sleeve. Unfortunately for you, this is the only shirt-making machine you have.
You have a choice of throwing your shirt-making machine away
and making no shirts at all, or keeping the machine and making some good shirts and some duds. All is not lost, however, because it will be pretty obvious which shirts to throw away: only the shirts that preserve a left-right symmetry are worth wearing. You will always be properly dressed if you let your machine make all kinds of shirts, but then keep only those shirts that have left-right symmetry.
The internal symmetry associated with forces accomplishes something analogous. It provides a useful marker to distinguish those quantities that we might in principle observe (the ones that involve the polarizations you want to keep) from those that should not be present (the ones involving the spurious polarization along the direction of motion). As with spam filters in computers that look for identifying features of unwanted e-mail to separate it from useful messages, the filter of internal symmetries distinguishes physical processes that preserve the symmetry from spurious ones that don’t. Internal symmetries make it easy to eliminate the spamlike polarizations; if they were present, they would break the internal symmetry.
The way the symmetry works is very similar to the colored spotlight example we discussed earlier, in which we could observe only the white light produced by the three colors together, not the individual lights. Similarly, it turns out that only certain combinations of particles are consistent with the internal symmetries involved in the theory of forces, and those are the only combinations that appear in the physical world.
The internal symmetries associated with forces ban any process involving the bad polarizations—the ones oscillating along the direction of motion (the ones that don’t really exist in nature). Just as the unbalanced shirts that were inconsistent with the left-right symmetry were readily distinguished and thrown away, the spurious polarizations that are inconsistent with the internal symmetry are automatically eliminated and never confuse calculations. A theory that stipulates the correct internal symmetry eliminates the bad polarizations that would otherwise be present.
Electromagnetism, the weak force, and the strong force are all communicated by gauge bosons: electromagnetism by the photon, the weak force by the weak gauge bosons, and the strong force by gluons. And each type of gauge boson is associated with waves that could in
principle oscillate in any direction, but in reality oscillate only in the perpendicular directions. So each of the three forces requires its own particular symmetry to eliminate the bad polarizations of the gauge bosons that communicate that force. There is therefore a symmetry associated with electromagnetism, an independent symmetry associated with the weak force, and still another symmetry associated with the strong force.
Internal symmetries in the theory of forces might seem complicated, but they are the simplest way physicists know to formulate a useful quantum field theory of forces that allows us to make predictions. The internal symmetries are what discriminate between the true and the spurious polarizations.
The internal symmetries we have just explored are critical to the theory of forces. They also underlie the Higgs mechanism, which tells us how elementary particles in the Standard Model acquire their mass. For the next chapter we will not need the details of the internal symmetry, but we will see that symmetry (and symmetry breaking) are essential components of the Standard Model.
Gauge bosons, Particles, and Symmetry
So far we’ve considered the effect of symmetry only on gauge bosons. But the symmetry transformations associated with a force do not act only on the gauge bosons. A gauge boson interacts with the particles that experience the force associated with that gauge boson: the photon interacts with electromagnetically charged particles, the weak bosons interact with weakly charged particles, and the gluons interact with quarks.
Because of these interactions, each of the internal symmetries can be preserved only if it transforms both the gauge bosons and the particles with which they interact. We can see this by analogy. Rotations, for example, wouldn’t be symmetry transformations if they acted on some objects but not others. If you rotate the top wafer of an Oreo cookie,
*
but not the rest of it, you would pull it apart. The
Oreo cookie would look the same after a rotation only if you were to rotate the entire thing simultaneously.
For similar reasons, a transformation that transformed only the gauge bosons that communicate a force, but not the particles that experience that force, could never preserve a symmetry. The internal symmetry that eliminates the spurious polarizations of the gluons requires the quarks to be interchangeable as well as the gluons. In fact, the symmetry transformation that interchanges quarks is the same one that interchanges the gauge bosons. The only way to preserve the symmetry is to mix up both together, just as the only way to preserve the Oreo cookie is to rotate the whole thing at the same time.
The force that will interest us most in this book is the weak force. The internal symmetry associated with the weak force treats the three weak gauge bosons as equivalent. It also treats particle pairs such as the electron and the neutrino, or the up and down quarks, as equivalent. This weak force symmetry transformation interchanges the three weak gauge bosons and also these pairs of particles. As with gluons and quarks, the symmetry is preserved only when everything is interchanged at once.
16
What to Remember
- Symmetries
tell us when two different configurations behave the same way. - In particle physics, symmetries are useful as a way of forbidding certain interactions: those that don’t preserve the symmetries are not allowed.
- Symmetries are important to the theory of forces because the simplest workable theory of forces includes a symmetry associated with each force. Those symmetries eliminate unwanted particles. They also eliminate the false predictions that the simplest theory of forces would otherwise make about high-energy particles.
