Warped Passages (74 page)

15
. Actually, according to special relativity’s underlying principles, there could have been a fourth polarization as well, one that would oscillate in the time direction. But that one doesn’t exist either, and the same internal symmetry that eliminates the third (longitudinal) polarization eliminates “time polarization” as well. Since it plays no role in the discussion in this or the following chapter, we won’t consider it any further.
16
. The true symmetries associated with all the forces are actually more subtle and rotate fields, which are complex quantities, into each other. The symmetries don’t merely interchange fields, they turn one field into a linear superposition of the others. The force associated with electromagnetism rotates a single complex field, whereas the weak force rotates two complex fields into each other, and the strong force rotates three.
17
. To make a Higgs model work, at least one of the Higgs fields must be forced to take a nonzero value. This would be true if the minimum energy configuration occurs when the value of at least one of the Higgs fields is nonzero. One way this can happen is illustrated in Figure M2, which shows the so-called Mexican hat potential, a plot of the energy the system would take for any combination of values of the two Higgs fields, where the two lower axes are the absolute values of the two Higgs fields and the height of the three-dimensional surface represents the energy of that particular configuration. This particular potential takes the form λ(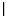 H
H
1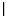 2
2
+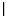 H
H
2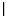 2
2
−
ν
2
)
2
, where λ determines how bowed up the potential is and
ν
determines the value that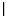 H
H
1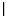 2
2
+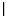 H
H
2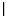 2
2
will take when the potential is at its minimum. The key feature of this potential is that when both fields have zero value, it is at a local maximum. Therefore, energy considerations tell us that the Higgs fields will not both be zero. Instead, they will take values that put them at the bottom of the circular basin surrounding the origin.
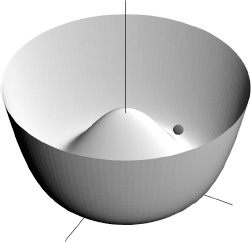
Figure M2.
The “Mexican hat” potential for the Higgs field.
18
. A more accurate way to describe the weak force symmetry would be to say that it rotates fields, rather than interchanging them.
19
. This actually simplifies the symmetry breaking. Even if both
x
and
y
were nonzero—if both
x
and
y
were 5, for example—the rotational symmetry would be broken since a particular direction is picked out, the direction pointing from
x
= 0,
y
= 0 to the point where
x
= 5 and
y
= 5. A similar “rotational” symmetry applies to Higgs
1
and Higgs
2
, but I have simplified and described the symmetry simply as an interchange symmetry. In the true description, even if both Higgs fields take the same value, the weak interaction symmetry would be broken—in much the same way as the point
x
= 5,
y
= 5 spontaneously breaks rotational symmetry.
20
. Although this model starts with two complex Higgs fields, there is only a single Higgs particle in the end. That is because the three other (real) fields become the three additional fields that are required to turn three massless particles with two physical polarizations into massive particles with three polarizations. Three of the Higgs fields become the third polarizations of the three heavy weak gauge bosons—the two Ws and the Z. The fourth remaining Higgs field should create true physical Higgs particles. If this model is right, the LHC should produce them.
21
. The strength of each of the forces is determined by a numerical coefficient. Renormalization group calculations show that the values of these quantities change logarithmically with energy.
22
. Whereas the weak force symmetry mixes pairs of fields and the strong
symmetry group mixes five fields. Some of the symmetry transformations associated with the forces of the GUT coincide with the weak symmetry and the strong symmetry transformations. The forces are unified because a single symmetry group of transformations includes all the symmetry transformations of the Standard Model.
23
. This connection to space and time is actually most manifest when two supersymmetry transformations are performed in succession, first in one order and then in the other, and then subtracted one from the other. In that case, fermions remain fermions and bosons remain bosons, but the system is moved; the net result of the transformation is exactly the same as a conventional spacetime transformation. The commutator of the two supersymmetry transformations, which perform exactly the same operation as a single spacetime symmetry transformation, decisively demonstrates that supersymmetry transformations must be connected to the symmetries that act on space and time and move things around.
