What If? (25 page)

Falling with Helium

Q.
What if I jumped out of an airplane with a couple of tanks of helium and one huge, un-inflated balloon? Then, while falling, I release the helium and fill the balloon. How long of a fall would I need in order for the balloon to slow me enough that I could land safely?
—Colin Rowe

A.
As ridiculous as it
sounds, this is—sort of—plausible.

Falling from great
heights is dangerous.
[
citation needed
]
A balloon could actually help save you, although a regular helium one from a party obviously won’t do the trick.

If the balloon is large enough, you don’t even need the helium. A balloon will act as a parachute, slowing your fall to nonfatal speeds.

Avoiding a high-speed landing is, unsurprisingly, the key to survival. As one medical paper put it
 . . . 

It is, of course, obvious that speed, or height of fall, is not in itself injurious . . . but a high rate of change of velocity, such as occurs after a 10 story fall onto concrete, is another matter.

 . . . which is just a wordy version of the old saying “It’s not the fall that kills you, it’s the sudden stop at the end.”

To act as a parachute, a balloon filled with air
—
rather than helium
—
would have to be 10 to 20 meters across, far too big to be inflated with portable tanks. A powerful fan could be used to fill it with ambient air, but at that point, you may as well just use a parachute.

Helium

Th
e helium makes things easier.

It doesn’t take too many helium balloons to lift a person.
In 1982, Larry Walters flew across Los Angeles in a lawn chair lifted by weather balloons, eventually reaching several miles in altitude. After passing through LAX airspace, he descended by shooting some of the balloons with a pellet gun.

On landing, Walters was arrested, although the authorities had some trouble figuring out what to charge him with. At the time, an FAA safety inspector told
the
New York Times,
“We know he broke some part of the Federal Aviation Act, and as soon as we decide which part it is, some type of charge will be filed.”

A relatively small helium balloon
—
certainly smaller than a parachute
—
will suffice to slow your fall, but it still has to be huge by party balloon standards.
Th
e biggest consumer rental helium tanks are about 250 cubic feet, and you would
need to empty at least ten of them to put enough air in the balloon to support your weight.

You’d have to do it quickly. Compressed helium cylinders are smooth and often quite heavy, which means they have a high terminal velocity. You’ll have only a few minutes to use up all the cylinders. (As soon as you emptied one, you could drop it.)

You can’t get around this problem by moving your
starting point higher. As we learned from the steak incident, since the upper atmosphere is pretty thin, anything dropped from the stratosphere or higher will accelerate to very high speeds until it hits the lower atmosphere, then fall slowly the rest of the way.
Th
is is true of everything from small meteors
1
to Felix Baumgartner.

But if you inflated the balloons quickly, possibly by connecting many canisters to it at once, you’d be able to slow your fall. Just don’t use too much helium, or you’ll end up floating at 16,000 feet like Larry Walters.

While researching this answer, I managed to lock up my copy of
Mathematica
several times on balloon-related differential equations, and subsequently got my IP address
banned from Wolfram|Alpha for making too many requests.
Th
e ban-appeal form asked me to explain what task I was performing that necessitated so many queries. I wrote, “Calculating how many rental helium tanks you’d have to carry with you in order to inflate a balloon large enough to act as a parachute and slow your fall from a jet aircraft.”

Sorry, Wolfram.

Everybody Out

Q.
Is there enough energy to move the entire current human population off-planet?
—Adam

A.
Th
ere are a bunch
of science fiction movies where, because of pollution, overpopulation, or nuclear war, humanity abandons Earth.

But lifting people into space is hard. Barring a massive reduction in the population, is launching the whole human race into space physically
possible? Let’s not even worry about where we’re headed
—
we’ll assume we don’t have to find a new home, but we can’t stay here.

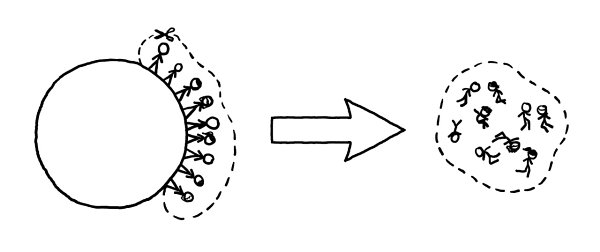
To figure out if this is plausible, we can start with an absolute baseline energy requirement: 4 gigajoules per person. No matter how we do it, whether we use rockets or a cannon or a space elevator or a ladder, moving a 65-kilogram person
—
or 65 kilograms of anything
—
out of the Earth’s gravity well requires at least this much energy.

How much is 4 gigajoules? It’s about a megawatt-hour,
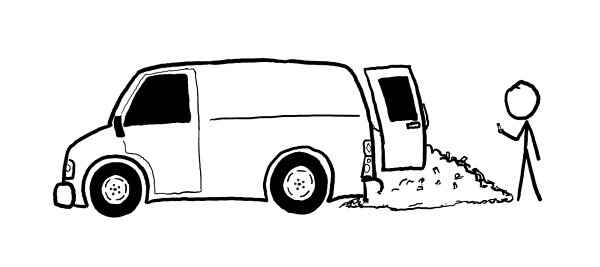
which is what a typical US household consumes in electricity in a month or two. It’s equal to the amount of stored energy in 90 kg of gasoline or a cargo van full of AA batteries.

Four gigajoules times seven billion people gives us 2.8×10
18
joules, or 8 peta-watt-hours.
Th
is is about 5 percent of the world’s annual energy consumption. A lot, but not physically implausible.

However, 4 gigajoules is just a minimum. In practice, everything would depend on our means of transportation. If we were using rockets, for example, it would take a lot more energy
than that.
Th
is is because of a fundamental problem with rockets:
Th
ey have to lift their own fuel.

Let’s return for a moment to those 90 kilograms of gasoline (about 30 gallons), because they help illustrate this central problem in space travel.

If we want to launch a 65-kilogram spaceship, we need the energy of around 90 kilograms of fuel. We load that fuel on board
—
and now our spaceship
weighs 155 kilograms. A 155-kilogram spaceship requires 215 kilograms of fuel, so we load another 125 kilograms on board . . . 

Fortunately, we’re saved from an infinite loop
—
where we add 1.3 kilograms for every 1 kilogram we add
—
by the fact that we don’t have to carry that fuel all the way up. We burn it as we go, so we get lighter and lighter, which means we need less and less fuel. But
we do have to lift the fuel partway.
Th
e formula for how much propellant we need to burn to get moving at a given speed is given by the Tsiolkovsky Rocket equation:

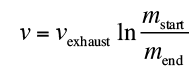
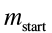and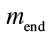
are the total mass of the ship plus the fuel before and after the burn, and
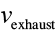is the “exhaust velocity” of the fuel, a number that’s between 2.5 and 4.5 km/s for rocket fuels.

What’s important is the ratio between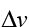
, the speed we want to be going, and
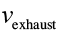, the speed that the propellant exits our rocket. For leaving Earth, we need a
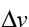of upward of 13 km/s, and
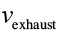is limited to about 4.5 km/s,
which gives a fuel-to-ship ratio of at least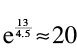
. If that ratio is x, then to launch a kilogram of ship, we need e
x
kilograms of fuel.