Why Beauty is Truth (38 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Lie's dream of a “Galois theory” of differential equations was eventually realized with the creation of a theory of “differential fields” in the early 1900s. But the theory of Lie groups turned out to be far more important, and more widely applicable, than Lie expected. Instead of being a tool to determine whether a differential equation can be solved in specific ways, the theory of Lie groups and Lie algebras has pervaded almost every
branch of mathematics. “Lie theory” escaped its creator and became greater than he ever imagined.
In hindsight, the reason is symmetry. Symmetry is deeply involved in every area of mathematics, and it underlies most of the basic ideas of mathematical physics. Symmetries express underlying regularities of the world, and those are what drive physics. Continuous symmetries such as rotations are closely related to the nature of space, time, and matter; they imply various conservation laws, such as the law of conservation of energy, which states that a closed system can neither gain nor lose energy. This connection was worked out by Emmy Noether, a student of Hilbert.
The next step, of course, is to understand the possible Lie groups, just as Galois and his successors sorted out many properties of finite groups. Here a second mathematician joined in the hunt.

Anna Catharina was worried about her son.
Her doctor had told her that young Wilhelm was “quite weakly and besides very awkward” and “always excited, but a completely impractical bookworm.” Wilhelm's health improved as he grew, but his bookworm tendencies did not. Just before his 39th birthday, he would publish a piece of mathematical research that has been described, with justification, as “the greatest mathematical paper of all time.” Such designations are of course subjective, but Wilhelm's paper would certainly be high on anyone's list.
Wilhelm Karl Joseph Killing was the son of Josef Killing and Anna Catharina Kortenbach. He had one brother, Karl, and one sister, Hedwig. Josef was a legal clerk, and Anna was a pharmacist's daughter. They were married in Burbach, on the eastern side of central Germany, and soon afterward moved to Medebach when Josef became the mayor there. Then he was made mayor of Winterberg, and after that mayor of Rüthen.
The family was quite well off and could afford a private tutor to prepare Wilhelm for the gymnasium, which in his case was in Brilon, 50 miles west of Dortmund. At school he liked classicsâLatin, Hebrew, Greek. A teacher named Harnischmacher introduced him to mathematics; Wilhelm turned out to be very good at geometry, and resolved to become a mathematician. He attended what is now the Westphalian Wilhelm University of Münster, but was then merely a Royal Academy. The academy did not teach advanced mathematics, so Killing taught himself. He read Plücker's
geometrical work and tried to derive some new theorems of his own. He also read Gauss's
Disquisitiones Arithmeticae.
After two years at the Royal Academy he moved to Berlin, where the quality of mathematical teaching was much superior, and came under the influence of Weierstrass, Kummer, and Hermann von Helmholtz, a mathematical physicist who clarified the link between conservation of energy and symmetry. Killing wrote a PhD thesis on the geometry of surfaces, based on some ideas of Weierstrass, and took a job as a teacher of mathematics and physics, with a sideline in Greek and Latin.
In 1875, he married a music lecturer's daughter, Anna Commer. Their first two children, both sons, died in infancy; the next two, daughters named Maria and Anka, thrived. Later, Killing fathered two more sons.
By 1878, he had gone back to his old school, but now as a teacher. He had a heavy workload, about 36 contact hours per week, but somehow he found the time to continue his mathematical researchâthe greats always do. He published a series of important papers in top journals.
In 1882, Weierstrass secured Killing a professorship at the Lyceum Hosianum in Braunsberg, where he spent the next ten years. Braunsberg had no strong mathematical tradition and offered no colleagues with whom to discuss research, but Killing seems not to have needed such stimulation. For it was there that he made one of the most important discoveries in the whole of mathematics. It left him rather disappointed.
What he had hoped to achieve was hugely ambitious: a description of
all possible
Lie groups. The Lyceum did not buy the journals in which Lie published, and Killing had very little idea of Lie's work, but he independently discovered the role of Lie algebras in 1884. So Killing knew that each Lie group was associated with a Lie algebra, and he quickly recognized that Lie algebras would probably be more tractable than Lie groups, so his problem reduced to the classification of all possible Lie algebras.
This problem turns out to be desperately hardâwe now know that it probably has no sensible answer, in the sense that no simple construction can produce all Lie algebras by a uniform and transparent procedure. So Killing was forced to settle for something far less ambitious: to describe the basic building blocks from which all Lie algebras can be assembled. This is a bit like wanting to describe all possible architectural styles but having to settle for a list of all possible shapes and sizes of brick.
These basic building blocks are known as
simple
Lie algebras. They are distinguished by a very similar property to Galois's idea of a simple group, one with no normal subgroups except trivial ones. In fact, a simple Lie group has a simple Lie algebra, and the converse is very nearly true as well. Amazingly, Killing succeeded in listing all possible simple Lie algebrasâmathematicians call such a theorem a “classification.”
In Killing's eyes, that classification was a very limited version of something far more general, and he was frustrated by several restrictive assumptions he had been forced to make in order to get anywhere. He was particularly irked by the need to assume simplicity, which forced him to switch to Lie algebras over the complex numbers rather than the reals. The former are better behaved but less directly related to the geometrical problems that fascinated Killing. Because of these self-imposed limitations, he did not consider his work worth publishing.
He did manage to make contact with Lie; not very fruitfully, as it turned out. First he wrote to Klein, who put him in touch with Lie's assistant Friedrich Engel, then working in Christiania. Killing and Engel hit it off immediately, and Engel became a staunch supporter of Killing's work, helped him get over some tricky points, and encouraged him to push the ideas further. Without Engel, Killing might have given up.
At first, Killing thought he knew the complete list of simple Lie algebras, and that these were the Lie algebras so(
n
) and su(
n
) associated with two infinite families of Lie groups: the special orthogonal groups SO(
n
), consisting of all rotations in
n
-space, and their analogues SU(
n
) in complex
n
-space, the special unitary groups. The historian Thomas Hawkins imagined “the amazement with which Engel read Killing's letter with its bold conjectures. Here was an obscure professor at a Lyceum dedicated to the training of clergymen in the far-away reaches of East Prussia, discoursing with authority and conjecturing profound theorems on Lie's theory of transformation groups.”
In the summer of 1886, Killing visited Lie and Engel at Leipzig, where both now worked. Unfortunately, there was some friction between Lie and Killing; Lie never really appreciated Killing's work and generally tried to play down its significance.

Killing quickly discovered that his original conjecture about simple Lie algebras was wrong, for he discovered a new one, whose corresponding Lie
group is now known as G
2
. It had 14 dimensions, and unlike the special linear and orthogonal Lie algebras, it did not seem to belong to an infinite family. It was a lone exception.
If this was strange, the final classification, which Killing completed in the winter of 1887, was stranger. To the two infinite families Killing added a third, the Lie algebras sp(2
n
) of what are now known as the symplectic groups Sp(2
n
). (Nowadays, we split the orthogonal groups into two different subfamilies, those acting on spaces of even dimension and those acting on spaces of odd dimension, yielding four families. There are reasons for doing this.) And now the exception G
2
had acquired five companions: two of dimension 56, and a short family that petered out, with dimensions 78, 133, and 248.
Killing's classification proceeded by a lengthy algebraic argument, which reduced the entire question to a beautiful problem in geometry. From a hypothetical simple Lie algebra he conjured up a configuration of points in a multidimensional space, known today as a
root system.
For exactly three of the simple Lie algebras, the root system lives in a space of two dimensions. These root systems look like this:
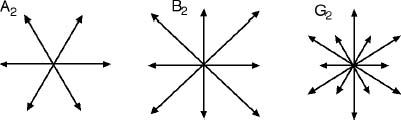
The root systems in two dimensions.
These patterns have a great deal of symmetry. In fact, they are reminiscent of the patterns you see in a kaleidoscope, where two mirrors set at an angle create multiple reflections. The similarity is no coincidence, because root systems have wonderful, elegant symmetry groups. Now known as Weyl groups (unfair, since they were invented by Killing), they are multidimensional analogues of the patterns formed by reflecting objects in a kaleidoscope.
The underlying structure of Killing's proof is that the search for all possible simple Lie algebras can be carried out by breaking the algebras into nice pieces, analogous to structures found in su(
n
). The classification then reduces to the geometry of those pieces, using their wonderful symmetries. Having sorted out the geometry of those pieces, you can now
bootstrap your results back to the problem you really wanted to solve: finding the possible simple Lie algebras.
As Killing put it, “The roots of a simple system correspond to a simple group. Conversely, the roots of a simple group can be regarded as determined by a simple system. In this way one obtains the simple groups. For each
l
there are four structures, supplemented for
l
= 2, 4, 6, 7, 8 by exceptional simple groups.”
Here “group” was a shortened form of “infinitesimal group,” which we now call a Lie algebra, and
l
is the dimension of the root system.
The four structures that Killing refers to are the Lie algebras su(
n
), so(2
n
), so(2
n
+1), and sp(2
n
) corresponding to families of groups SU(
n
), SO(2
n
), SO(2
n
+1), and Sp(2
n
): the unitary groups, the orthogonal groups in spaces of even dimension, the orthogonal groups in spaces of odd dimension, and the symplectic groups in spaces of even dimension. The symplectic groups are the symmetries of the positionâmomentum variables introduced by Hamilton in his formulation of mechanics, and the number of dimensions there is always even because the variables come in positionâmomentum pairs. Aside from these four families, Killing claimed that exactly six other simple Lie algebras exist.
