Zero (30 page)

Let
a
and
b
each be equal to 1. Since
a
and
b
are equal,

b
²
=
ab
(eq. 1)

Since
a
equals itself, it is obvious that

a
²
=
a
²
(eq. 2)

Subtract equation 1 from equation 2. This yields

a
²
-
b
²
=
a
²
-
ab
(eq. 3)

We can factor both sides of the equation;
a
²
-
ab
equals
a
(
a
-
b
). Likewise,
a
²
-
b
²
equals (
a
+
b
)(
a
-
b
). (Nothing fishy is going on here. This statement is perfectly true. Plug in numbers and see for yourself!) Substituting into equation 3, we get

(
a
+
b
)(
a
-
b
) =
a
(
a
-
b
) (eq. 4)

So far, so good. Now divide both sides of the equation by (
a
-
b
) and we get

a
+
b
=
a
(eq. 5)

Subtract
a
from both sides and we get

b
= 0 (eq. 6)

But we set
b
to 1 at the very beginning of this proof, so this means that

1 = 0 (eq. 7)

This is an important result. Going further, we know that Winston Churchill has one head. But one equals zero by equation 7, so that means that Winston has no head. Likewise, Churchill has zero leafy tops, therefore he has one leafy top. Multiplying both sides of equation 7 by 2, we see that

2 = 0 (eq. 8)

Churchill has two legs, therefore he has no legs. Churchill has two arms, therefore he has no arms. Now multiply equation 7 by Winston Churchill's waist size in inches. This means that

(Winston's waist size) = 0 (eq. 9)

This means that Winston Churchill tapers to a point. Now, what color is Winston Churchill? Take any beam of light that comes from him and select a photon. Multiply equation 7 by the wavelength, and we see that

(Winston's photon's wavelength) = 0 (eq. 10)

But multiplying equation 7 by 640 nanometers, we see that

640 = 0 (eq. 11)

Combining equations 10 and 11, we see that

(Winston's photon's wavelength) = 640 nanometers

This means that this photon—or any other photon that comes from Mr. Churchill—is orange. Therefore Winston Churchill is a bright shade of orange.

To sum up, we have proved, mathematically, that Winston Churchill has no arms and no legs; instead of a head, he has a leafy top; he tapers to a point; and he is bright orange. Clearly, Winston Churchill is a carrot. (There is a simpler way to prove this. Adding 1 to both sides of equation 7 gives the equation

2 = 1

Winston Churchill and a carrot are two different things, therefore they are one thing. But that's not nearly as satisfying.)

What is wrong with this proof? There is only one step that is flawed, and that is the one where we go from equation 4 to equation 5. We divide by
a
-
b.
But look out. Since
a
and
b
are both equal to 1,
a
-
b
= 1 - 1 = 0. We have divided by zero, and we get the ridiculous statement that 1 = 0. From there we can prove any statement in the universe, whether it is true or false. The whole framework of mathematics has exploded in our faces.

Used unwisely, zero has the power to destroy logic.

Divide a line in two, such that the ratio of the small part to the large part is equal to the ratio of the large part to the whole line. For the sake of simplicity, let's say that the small part is 1 foot long.

If the small part is 1 foot long, and the large part is
x
feet long, then the length of the whole line is obviously 1 +
x
feet long. Putting our relationship into algebra, we find that the ratio of the small part to the large part is

1/
x

while the ratio of the large part to the whole thing is

x
/(1 +
x
)

Since the ratio of the small to the large is equal to the ratio of the large to the whole, we can set the two ratios equal to each other, yielding the equation

x
/(1 +
x
) = 1/
x

We wish to solve the equation for
x,
which is the golden ratio. The first step is to multiply both sides by
x,
which yields

x
²
/(1 +
x
) = 1

We then multiply by (1 +
x
), which gives us the equation

x
²
= 1 +
x

Subtract 1 +
x
from both sides, yielding

x
²
-
x
- 1 = 0

Now we can solve the quadratic equation. This gives us two solutions:

Only the first one, with a value of about 1.618, is positive, thus it is the only one that made sense to the Greeks. Thus the golden ratio is approximately 1.618.

Nowadays, the derivative is on firm logical grounds, because we define it in terms of limits. The formal definition of a derivative of a function
f
(
x
) [which we denote as
f
'(
x
)] is

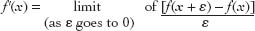
To see how this gets rid of Newton's dirty trick, let's look at the same function we used for demonstrating Newton's fluxions:
f
(
x
) =
x
²
+
x
+ 1. The derivative of this function is equal to

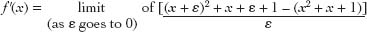
Multiplying out, we get

Now the
x
²
cancels out the -
x
²
, the
x
cancels out the -
x
, and the 1 cancels the - 1, leaving us with

Dividing through by ?—remember, ? is always nonzero because we haven't taken the limit yet—we get

f
'(
x
) = limit
(as ? goes to 0) of 2
x
+ 1 + ?

Now
we take the limit and let ? approach zero. We get

f
'(
x
) = 2
x
+ 1 + 0 = 2
x
+ 1

which is the answer we desired.

It's a small shift in thinking, but it makes all the difference in the world.

To show that the rational numbers are the same size as the natural numbers, all Cantor had to do was come up with a clever seating pattern. This is precisely what he did.

As you may recall, the rationals are the set of numbers that can be expressed as
a
/
b
for some integers
a
and
b
(with
b
nonzero, of course). To start with, let us consider the positive rational numbers.

Imagine a grid of numbers—two number lines crossed at zero, just like the Cartesian coordinate system. Let's put zero at the origin, and at every other point on that grid, let's associate with the rational number
x/y
where
x
is the point's
x
-coordinate and
y
is the point's
y
-coordinate. Since the number lines go off to infinity, every positive combination of
x
s and
y
s has a spot on that grid (Figure 58).

Now let's create a seating chart for the positive rational numbers. For seat one, let's start at 0 on the grid. Then let's move to 1/1: that's seat two. Next, wander over to ½: seat three. Then to 2/1 (which, of course, is the same thing as 2): seat four. Then to 3/1: seat five. We can wander back and forth along the grid, counting off numbers as we go. This yields a seating chart:

Figure 58: An enumeration of the rational numbers

Eventually, all the numbers have a seat; some, in fact, have two seats. It's easy to remove the duplicates—just skip over them when making the seating chart. The next step is to double the list, adding the negative rationals after the corresponding positive rational. This gives us a seating chart:

Now all the rational numbers—positives, negatives, and zero—have a seat. Since nobody is left standing and no seats are open, this means that the rationals are the same size as the counting numbers.