100 Essential Things You Didn't Know You Didn't Know (29 page)
Read 100 Essential Things You Didn't Know You Didn't Know Online
Authors: John D. Barrow

And so on, forever: every term in the sum exactly half the size of its predecessor. The sum of this series is actually equal to 1, but someone in the audience who wasn’t a mathematician wanted to know if there was any way to show him that this is true.
Fortunately, there is a simple demonstration that just uses a picture. Draw a square of size 1 × 1, so its area is 1. Now let’s divide the square in half by dividing it from top to bottom into two rectangles. Each of them must have an area equal to ½. Now divide one of these rectangles in two to make two smaller rectangles, each with
area
equal to one-quarter. Now divide one of these smaller rectangles in half to make two more rectangles, each of area equal to one-eighth. Keep on going like this, making a rectangle of half the area of the previous one, and look at the picture. The original square has just had its whole area subdivided into a never-ending sequence of regions that fill it completely. The total area of the square is equal to the sum of the areas of the pieces that I have left intact at each stage of the cutting process, and the areas of these pieces is just equal to our series S. So the sum of the series S must be equal to 1, the total area of the square.

Usually when we encounter a series like S for the first time, we work out its sum in another way. We notice that each successive term is one half of the previous one and then multiply the whole series by 1/2 so we have
½ × S = ¼ + ⅛ +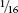 +
+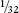 +
+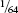 + . . .
+ . . .
But we notice that the series on the right is just the original series, S, minus the first term, which is ½. So we have that ½× S = S – ½, and S = 1 again.
93
Segregation and Micromotives
The world is full of obvious things which nobody by any chance ever observes.
Sherlock Holmes in
The Hound of the Baskervilles
In many societies there is a significant segregation between communities of different types – racial, ethnic, religious, cultural and economic. In some cases there is loudly stated dislike of one community by another, but in others there doesn’t seem to be any overt attempt to be separate and the different communities get on well as individuals in their spheres of activity. However, the tendencies of individuals may not be a good guide to the behaviour of a group because of the interplay between many individual choices. When some of the statistical methods used by scientists to study the collective behaviour of large numbers of things are applied to populations of people, some very simple but unexpected truths emerge.
In 1978 Thomas Schelling, an American political scientist, decided to investigate how racial segregation came about in American cities. Many people assumed that it was simply a result of racial intolerance. Some thought that it might be overcome by throwing different communities together in a random mix, but were surprised to find that the result was always segregation into different racial sub-communities again, even though the residents seemed to be quite
tolerant
of other ethnic groups when questioned in surveys. What emerged from a mathematical study of virtual societies using computer simulations was that very slight imbalances result in complete segregation despite an average tolerant outlook. Suppose that a family will move, because of intolerance or to avoid it, if more that one in three of its neighbours are different from them, but will stay put if fewer than one in five are different. In this situation a random mix of two sorts of families (‘blue’ and ‘red’) that differ in some way (race, religion or class, say) will gradually become more and more polarised, until eventually it is completely segregated into a totally blue and a totally red community, just like a mixture of oil and water,
fn1
with empty ‘buffer’ regions between them. In a region with above average reds the blues move, leading to above average blues elsewhere, so the reds in that new above average blue neighbourhood move out, and so on. The moves all tend to be towards regions where there is an above average concentration of the mover’s type. The boundary regions between different regions are always very sensitive since single movers can tip the balance one way or the other. It is more stable to evolve towards these boundary regions being empty to create a buffer between the segregated communities.
These simple insights were very important. They showed that very strong segregation was virtually inevitable in mixed communities and didn’t imply that there was serious intolerance. Segregation doesn’t necessarily mean prejudice – although it certainly can, as the examples of the United States, Rhodesia, South Africa and Yugoslavia show. Better to foster close links between the separate communities than to try to prevent them forming. Macrobehaviour is fashioned by micromotives that need not be part of any organised policy.
fn1
Actually, this familiar example should not be examined too closely. If the dissolved air is removed from water, say by repeated freezing and thawing, it
will
mix with oil quite smoothly.
94
Not Going with the Flow
Email is a wonderful thing for people whose role in life is to be on top of things. But not for me; my role is to be on the bottom of things.
Don Knuth
We have seen in the previous chapter an example of collective behaviour where no individual wants to find themselves in a significant minority. Not all situations are like this. If you are wanting to get away from it all at an idyllic island holiday destination, you want to be in the minority, not the majority, when it comes to everyone’s holiday destination of choice. The pub that ‘everyone’ chooses to go to because of the music or the food is going to turn out to be a far from ideal experience if you have to queue to get in, can’t find a chair and have to wait an hour to be served. You will do better at a less popular venue.
This is like playing a game where you ‘win’ by being in the minority. Typically, there will be an average number of people who choose to go to each of the venues on offer, but the fluctuations around the average will be very large. In order to reduce them and converge on a strategy that is more useful, it is necessary to use past information about the attendance at the venue. If you just try to guess the psychology of fellow customers, you will end up committing the usual sin of assuming that you are not average. You think that your choice will not also be made by
lots
of other people acting on the same evidence – that’s why you find that everyone else has decided to go for the same stroll by the river on a sunny Sunday afternoon.
If there are two venues to choose between, then as a result of everyone’s accumulated experience the optimal strategy gets closer and closer to half of the people going to each venue – so neither is specially popular or unpopular – on the average. At first, the fluctuations around the average are quite large, and you might turn up at one venue to find a smaller than average crowd. As time goes on, you use more and more past experience to evaluate when and if these fluctuations will occur and act accordingly, trying to go to the venue with the smaller number. If everyone acts in this way, the venue will maintain the same average number of attendees over time but the fluctuations will steadily diminish. The last ingredient of this situation is that there will be players who trust their memories and analyses of past experience, and there will be others who don’t or who only appeal to experience a fraction of the times when they have to make a choice. This tends to split the population into two groups – those who follow past experience totally and those who ignore it. Since the consequences of making the wrong choice are far more negative (no dinner, wasted evening) than the consequences of making the right choice are positive (quicker dinner, more comfortable evening), greater care is made to avoid wrong choices, and players tend to hedge their bets and go for each available choice with equal probability over the long run. Adopting a more adventurous strategy results in more extreme losses than gains. The result is a rather cautious and far from optimal pattern of group decision making and all the eating venues are less than full.
95
Venn Vill They Ever Learn
There are two groups of people in the world; those who believe that the world can be divided into two groups of people, and those who don’t.
Anon.
John Venn came from the east of England, near the fishing port of Hull, and went – as promising mathematicians did – to Cambridge, where he entered Gonville and Caius College as a student in 1853. Graduating among the top half-dozen students in mathematics, he was elected into a college teaching fellowship. He then left the college for four years and was ordained a priest in 1859, following in the line of his distinguished father and grandfather, who were prominent figures in the evangelical wing of the Anglican Church. However, instead of following the ecclesiastical path that had been cleared for him, he returned to Caius in 1862 to teach logic and probability. Despite this nexus of chance, logic and theology, Venn was also a practical man and rather good at building machines. He constructed one for bowling cricket ball which was good enough to clean bowl one of the members of the Australian touring cricket team on four occasions when they visited Cambridge in 1909.
It was his college lectures in logic and probability that made Venn famous. In 1880 he introduced a handy diagram for representing logical possibilities. It soon replaced alternatives that had
been
tried by the great Swiss mathematician Leonard Euler and the Oxford logician and Victorian surrealist writer Lewis Carroll. It was eventually dubbed the ‘Venn diagram’ in 1918.
Venn’s diagrams represented possibilities by regions of space. Here is a simple one that represents all the possibilities where there are two attributes.

