100 Essential Things You Didn't Know You Didn't Know (5 page)

After you have acquired 40 different cards there will be a 10/50 chance that the next one will be one you haven’t already got. So on the average you will have to buy another 50/10, or 5 more cards to have a better than evens chance of getting another new one that you need for the set. Therefore, the total number of cards you will need to buy on average to get the whole set of 50 will be the sum of 50 terms:

50/50 + 50/49 + 50/48 + . . . + 50/3 + 50/2 + 50/1

where the first term is the certain case of the first card you get and each successive term tells you how many extra cards you need to buy to get the 2nd, 3rd and so on missing members of the set of 50 cards.

As there can be collections with all sorts of different numbers of cards in them, let’s consider acquiring a set with any number of cards in it, that we will call N. Then the same logic tells us that on the average we will have to buy a total of

(N/N) + (N/N-1) + (N/N-2) + . . . + N/2 + N/1 cards

Taking out the common factor N in the numerators of each term, this is just

N(1 + 1/2 + 1/3 + . . . + 1/N).

The sum of terms in the brackets is the famous ‘harmonic’ series. When N becomes large it is well approximated by 0.58 + ln(N) where ln(N) is the natural logarithm of N. So as N gets realistically large we see that the number of cards we need to buy on the average to complete our set is about

Cards needed ≈ N × [0.58 + ln(N)]

For my sets of 50 motor car cards the answer is 224.5, and I should have expected to have to have bought on average about 225 cards to make up my set of 50. Incidentally, our calculation shows how much harder it gets to complete the second half of the collection than the first half. The number of cards that you need to buy in order to collect N/2 cards for half a set is

(N/N) + (N/N-1) + (N/N-2) + . . . + N/(½N+1)

which is the difference between N times the harmonic series summed to N and summed to N/2 terms, so

Cards needed for half a set ≈ N × [ln(N) + 0.58 – ln(N/2) – 0.58] = Nln(2) = 0.7N

Or just 35 to get the first half of my set of 50.

I wonder if the original manufacturers performed such calculations. They should have, because they enable you to work out the maximum possible profit you could expect to gain in the long run from marketing a particular size set of cards. It is likely to be a maximum
possible
profit only because collectors will trade cards and be able to acquire new cards by swopping rather than buying new ones.

What impact can friends make by swopping duplicates with you?

Suppose that you have F friends and you all pool cards in order to build up F+1 sets so that you have one each. How many cards
would
you need to do this? On the average, when the number of cards N is large, and you share cards, the answer approaches

N × [ln(N) + F ln(lnN) + 0.58]

On the other hand, if you had each collected a set without swopping, you would have needed about (F+1)N[ln(N) + 0.58] cards to complete F+1 separate sets. For N = 50, the number of card purchases saved would be 156F. Even with F = 1 this is a considerable economy.

If you know a little statistics you might like to show that the deviation that can be expected on the N × [0.58 + ln(N)] result is close to 1.3N. This is quite significant in practice because it means that you have a 66% chance of needing to collect 1.3 N more or less than the average. For our 50-card set this uncertainty in the expected number of purchases is 65. There was a story a few years ago that a consortium was targeting suitable national lotteries by calculating the average number of tickets that needed to be bought in order to have a good chance of collecting all the possible numbers – and so including the winning one. The members neglected to include the likely variance away from the average result but were very lucky to find that they did have a winning ticket among the millions they had bought.

If the probability of each card appearing is not the same, then the problem becomes harder but is still soluble. In that case it is more like the problem of coin collecting where you try to collect a coin with each available year date on. You don’t know whether equal numbers were minted in each year (almost certainly they weren’t) or how many may have been withdrawn later, so you can’t rely on there being an equal chance of collecting an 1840 penny or an 1890 one. But if you do find a 1933 English penny (of which only 7 were made and 6 are accounted for) then be sure to let me know.

13

Tally Ho

It is a profoundly erroneous truism . . . that we should cultivate the habit of thinking of what we are doing. The precise opposite is the case. Civilization advances by extending the number of important operations which we can perform without thinking about them.

Alfred North Whitehead

The hopeless prisoner is incarcerated in a dark, dank, forgotten cell. The days, months and years are passing slowly. There are many more to come. The scene is familiar from the movies. But there is usually an interesting mathematical sub-text. The prisoner has been keeping track of the days by systems of marks on the cell wall. The oldest human artefacts with records of counting in Europe and Africa go back more than 30,000 years and show similar elaborate groups of tally marks following the days of the month and the accompanying phases of the Moon.

The standard European pattern of tallying goes back to finger counting and results in sets of 4 vertical(ish) lines | | | | being completed by a cross slash to signal a score of five. On to the next set of five
and so on. The vertical bars plus slash denoting each counted item show ways of counting that predate our formal counting systems and led to the adoption of the Roman numerals I, II and III or the simple Chinese rod numeral systems. They are closely linked to simple methods of finger counting and make use
of
groups of 5 and 10 as bases for the accumulated sets of marks. Ancient tallying systems recorded marks on bone or were notches carved in wood. Single notches recorded the first few, but a half-cross notch V was then used to mark the 5, with a complete cross X for the ten, hence the V and X Roman numerals; 4 was made either by addition as IIII, or by subtraction as IV. Tallying remained a serious official business in England until as late as 1826, with the Treasury using great wooden tally sticks to keep records of large sums entering and leaving the Exchequer. This use is also the source of the multiple meanings of the word ‘score’, which means to make a mark and to keep count, as well as the quantity 20. The word tally comes from the word for cut, as still in ‘tailor’. When a debt was owed to the Treasury, the tally stick with its scored marks was cleft down the middle and the debtor given one half, the Treasury the other. When the debt was settled the two pieces were joined to check that they ‘tallied’.

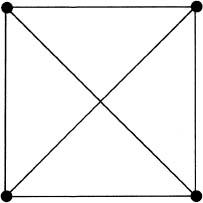
Counting these tally marks is rather laborious, especially if large totals arise. Individual marks have to be mentally counted and then the number of sets has to be totalled as well. In South America we find the occasional use of a memorable system that uses a gradual build-up of numbers by lines around a square, completed by the two diagonals
.

We are familiar with a variant of this square frame counting when we keep score in a cricket match by making six marks in three rows of two – a ‘dot’ if no run is scored, or the number scored, or a ‘w’ if a wicket falls. Other symbols denote wides, byes, no-balls and leg byes. If no runs are scored off all six balls, the six dots are joined up to create the sides of an M, denoting a ‘maiden’ over; if no runs are scored and a wicket is taken, they are joined to form a W, to indicate a ‘wicket maiden’ over. In this way a glance at the score book reveals the pattern and number of runless overs.

It is tempting to combine the insights from South American games with those of the cricket scorer to create an ideal aide-memoire for
anyone
wanting to tally in tens and not have to count up to ten vertical marks to ‘see’ where the running total has reached. First count from 1 to 4 by placing dots at the four corners of a square, keep on counting from 5 to 8 by adding the four sides, and count 9 and 10 by adding the two diagonals. Each set of 10 is represented by the completed square of four dots and 6 lines. For the next 10 move on to a new square. Completion of a ten is obvious at a glance.

14

Relationships

Relationship:
The civilised conversationalist uses this word in public only to describe a seafaring vessel carrying members of his family.

Cleveland Amory

Most magazines have endless articles and correspondence about relationships. Why? Answer: Relationships are complicated, sometimes interesting and can often appear unpredictable. This is just the type of situation that mathematics can help you with.

The simplest relationships between things have a property that we call ‘transitivity’ and it makes life simple. Being ‘taller than’ is one of these transitive relationships. So if Ali is taller than Bob and Bob is taller than Carla, then Ali is necessarily taller than Carla. This relationship is a property of heights. But not all relations are like this. Ali might like Bob and Bob might like Carla, but that does not mean that Ali likes Carla. These ‘intransitive’ relations can create very unusual situations when it comes to deciding what you should do when everyone does not agree.

Suppose that Ali, Bob and Carla decide to invest together in a second-hand car and go out to look at three different possibilities: an Audi, a BMW and a Reliant Robin. They don’t all agree on what to buy, so they decide that the outcome must be decided democratically. They must vote on it. So, each of them writes down their order of preference for the three makes:

The voting looks promising at first: Audi beats BMW by 2 preferences to 1, and BMW beats the Reliant Robin by 2 preferences to 1. But, strangely, the Reliant Robin beats the Audi by 2 preferences to 1. Preferring, like ‘admiring’, is an intransitive relationship that can create awkward paradoxes if not used with care. Small elections to decide who you prefer among candidates for a job, who captains a sports team or even what car to buy are fraught with paradox. Let the voter beware.

Faced with this trilemma, Ali, Bob and Carla decided to give up on the car buying and put their resources into renting a house together. Alas, more decisions were soon necessary. Should they decorate the living room? Should they tidy the garden? Should they buy a new TV? There was no consensus so they decided to vote ‘yes’ or ‘no’ on each of the three issues in turn. Here’s what they said: