Alex’s Adventures in Numberland (31 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Only the digit 8 seems a little overabundant, yet the difference is statistically insignificant. It would appear that pi is normal, yet no one has been able to prove it. And neither has anyone been able to prove that such a proof is impossible. There is a chance, therefore, that pi is
not
normal. Maybe after 10
20
there really are just 0s and 1s?
A different, but related issue, is the positioning of the numbers. Are they distributed randomly? Stan Wagon analysed the first ten million digits of pi with a ‘poker test’: take five consecutive digits and consider them as if they are a poker hand.
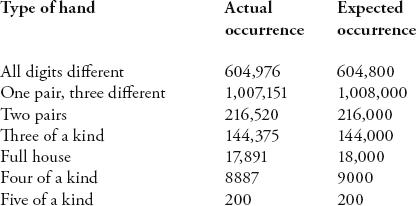
The right column is how many times we would expect to see the poker hands if pi was normal and each decimal place had an equal chance of being occupied by any digit. The results are well within the boundaries of what we would expect. Each pattern of numbers seems to appear with the frequency it would had each decimal place been randomly generated.
There are websites that can find you the first occurrence in pi of the numbers of your birthday. The first time the sequence 0123456789 occurs is at the 17,387,594,880th place – which was discovered only when Kanada got that far in 1997.
I asked Gregory if he ever believed an order would be found in pi. ‘There is no order,’ he replied dismissively. ‘And if there would be an order, it would be weird and not right. So there is no point wasting the time.’
Instead of focusing on patterns in pi, some see its very randomness as a tremendous expression of mathematical beauty. Pi is predetermined but it seems to mimic randomness extraordinarily well.
‘It is a very good random number,’ agreed Gregory.
Shortly after the Chudnovskys started computing pi they got a call from the United States government. David squealed an impersonation of the voice at the end of the line: ‘Could you please send pi?’
Random numbers are needed in industry and commerce. For example, just say a market-research company needs to poll a representative sample of a thousand people from a population of a million. The company will use a random-number generator to select the sample group. The better the generator is at providing random numbers, the more representative the sample will be – and the poll will be more accurate. Likewise, streams of random numbers are needed to simulate unpredictable scenarios when testing computer models. The more random the numbers, the more robust the testing will be. In fact, projects can fail if the random numbers used to test them are not random enough. ‘You are only as good as your random number,’ remarked David. ‘If you use terrible random numbers, you will end up in a terrible condition,’ concluded Gregory. Of all sets of available random numbers, the decimal expansion of pi is the best.
Yet there is a philosophical paradox. Pi is self-evidently not random. Its digits may behave like random digits, but they are fixed. For example, if the digits in pi were truly random then there would be only a 10 percent chance that the first digit after the decimal point is a 1, yet we know that it is 1 with absolute certainty. Pi exhibits randomness non-randomly – which is fascinating, and weird.
Pi is a mathematical concept that has been studied for thousands of years, yet it holds many secrets. There have been no great advances in understanding its nature since transcendence was proved almost a century and a half ago.
‘We actually don’t know about most of this stuff,’ said Gregory.
I asked if there would ever be a new advance in understanding pi.
‘Of course, of course,’ said Gregory, ‘There are always advances. Mathematics moves forward.’
‘It will be more miraculous but it won’t be nice,’ David said.
Nineteen sixty-eight was a year of counter-cultural uprisings around the world, and Britain was not immune to such generational upheaval. In May the Treasury announced the introduction of a revolutionary new coin.
The 50p piece was designed to replace the old ten-shilling note as part of the switch from imperial to decimal currency. Yet what set the coin apart was not its denomination, but its unorthodox shape.
‘It’s no ordinary coin,’ exhorted the
Daily Mirror
. ‘Why, the Decimal Currency Board even go so far as to call it a “multilateral-curve heptagon”.’ Never before had a country introduced a seven-sided coin. And never before had a nation been so outraged over the aesthetics of a geometric shape. Leading the foment was retired army colonel Essex Moorcroft, of Rosset, Derbyshire, who formed the Anti-Heptagonists. ‘We take our motto from Cromwell’s heartfelt cry, “Take away this bauble”. I have founded the society because I believe our Queen is insulted by this heptagonal monstrosity,’ he said. ‘It is an ugly coin and an insult to our Sovereign, whose image it bears.’
Nonetheless, the 50p entered circulation in October 1969, and Colonel Moorcroft did not take to the barricaes. Indeed, by January 1970
The Times
reported that ‘the curvaceous heptagon seems to have won for herself some affection’. Today the 50p piece is considered a distinctive and cherished part of British heritage. When a 20p piece was introduced in 1982, it too was heptagonal.
The 50p and 20p pieces are, in fact, design classics. Their seven-sided shape means that they are easily distinguished from circular coins, helping in particular the blind and partially sighted. They are also the most thought-provoking coins in circulation. The circle is not the only interesting round shape in mathematics.
A circle can be defined as a curve for which every point is equidistant from a fixed point, the centre. This property has many practical applications. The wheel – generally trumpeted as humanity’s first great invention – is the most obvious. An axle attached to the centre of a wheel will stay at a fixed point above the ground when the wheel rotates smoothly along a surface, which is why carts, cars and trains run smoothly without bobbing up and down.
For the transportation of very heavy loads, however, an axle might not take the weight. One alternative is to use rollers. A roller is a long tube with a circular cross-section, laid out on the ground. If a heavy object with a flat base (such as a giant cuboidal piece of stone intended for a pyramid) is put on several rollers, then it can be pushed smoothly over the rollers, with new rollers being put in front as it inches forward.
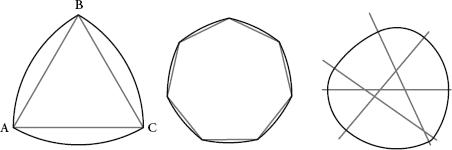
Curves of constant width include the Reuleaux triangle (left) and the multilateral-curve heptagon, better known as the 50p piece (centre).
The crucial feature of a roller is that the distance between the ground and the top of the roller is always the same. This is obviously the case with a circular cross-section, since the width of a circle (the diameter) is always the same.
Do all rollers have to have a circular cross-section? Are there any other shapes that will work? It may appear counter-intuitive, but there are, in fact, a variety of shapes that will make perfect rollers. An example is the 50p piece.
If you welded coins together to form rollers that had a 50p piece as a cross-section and then placed this book on these rollers, the book would not wobble up and down as you pushed it along. It would ride as smoothly as if on circular cylinders.
The reason this happens is because the 50p piece is a
curve of constant width
. Wherever you measure it around its perimeter, the 50p has the same breadth. So, when a 50p rolls along the floor, the distance from the floor to the top of the coin is always equal. A book lying atop a set of 50p rollers therefore stays at the same height.
Surprisingly, there are many, many curves of constant width. The simplest is the Reuleaux triangle. It is constructed from an equilateral triangle by putting the point of a compass at each vertex and drawing the arc that goes between the other two vertices. In the diagram above, put the compass at A and move the pencil from B to C, and then repeat with the other vertices. The multilateral-curve heptagon is constructed the same way. Curves of constant width do not need to be symmetrical. It is possible to construct them from any number of lines crossing, as shown above right. The sections of perimeter are always arcs of a circle centred in the opposing vertex.
The curvilinear triangle owes its name to Franz Reuleaux, a German engineer who first wrote about its applications in his 1876 book
Kinematics of Machinery
. This was read many years later by H.G. Conway, a former president of the Institution of Mechanical Engineers, who sat on the British Treasury’s Decimal Currency Board. Conway suggested a non-circular curve of constant breadth for the 50p piece since this property made it suitable for use in coin-operated machines. Machines distinguish coins by measuring diameter, and the 50p piece has the same width whichever position it is in. (A square coin, even with rounded sides, can never have constant width, which is why there are no four-sided coins.) Seven sides were chosen since it was considered the most aesthetically pleasing.
While the Reuleaux triangle reinvented the roller, it didn’t reinvent the wheel. Wheels cannot be made of Reuleaux triangles because non-circular curves of constant width do not have a ‘centre’ – a fixed point that is equidistant from every point on the perimeter. If you put an axle on a Reuleaux triangle and rolled it, the height of the shape would stay the same but the axle would judder around.
One useful property of a Reuleaux triangle is that it can be rotated inside a square so that it touches all four sides of the square at all times. This property was exploited by Harry James Watts, an English engineer living in Pennsylvania, in 1914, when he designed one of the most bizarre tools in existence: a drill that can drill square holes. (The corners are rounded, rather than sharp, so, strictly speaking, the hole is a modified square.)
The cross-section of Watts’s invention is simply a Reuleaux triangle, with three portions removed to make a cutting edge. It comes with a special chuck to compensate for the wobble of the drill bit’s centre as it rotates. The Watts square-hole drill is still used today.
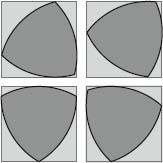
Reuleaux triangle rotating in square.

