Alex’s Adventures in Numberland (5 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

As more and more objects were tracked, our vocabulary and symbology of numbers expanded and – accelerating to the present day – we now have a fully developed system of exact numbers with which we can count as high as we like. Our ability to express numbers exactly, such as being able to say that there are precisely 75 dots in the top picture on the previous page, sits cheek-by-jowl with our more fundamental ability to understand such quantities approximately. We choose which approach to use depending on circumstance: in the supermarket, for example, we use our understanding of exact numbers when we look at prices of products. But when we decide to join the shortest checkout queue we are using our instinctive, approximate sense. We do not count every person in every queue. We look at the queues and estimate which one has the fewest people in it.
In fact, we use our imprecise approach to numbers constantly, even when using precise terminology. Ask someone how long it takes them to get to work and most often the answer will be a range, say, ‘Thirty-five, forty minutes.’ In fact, I have noticed that I am incapable of giving single-number answers to questions involving quantity. How many people were at the party? ‘Twenty, thirty…’ How long did you stay? ‘Three and a half, four hours…’ How many drinks did you have? ‘Four, five…
ten
…’ I used to think that I was just being indecisive. Now I’m not so sure. I prefer to think that I was drawing on my inner number sense, an intuitive, animal propensity to deal in approximations.
Since the approximate number sense is essential for survival, it might be thought that all humans would have comparable abilities. In a 2008 paper, psychologists at Johns Hopkins University and the Kennedy Krieger Institute investigated whether or not this was the case among a group of 14-year-olds. The teenagers were shown varying numbers of yellow and blue dots together on a screen for 0.2 seconds, and asked only whether there were more blue or yellow dots. The results astonished the researchers, since the scores showed an unexectedly wide variation in performance. Some pupils could easily tell the difference between 9 blue dots and 10 yellow, but others had abilities comparable to those of infants – hardly even able to say if 5 yellow dots beat 3 blue.
An even more startling finding became apparent when the teenagers’ dot-comparing scores were then compared to their maths scores since kindergarten. Researchers had previously assumed that the intuitive ability to discriminate amounts does not contribute much to how good a student is at tasks such as solving equations and drawing triangles. Yet this study found a strong correlation between a talent at reckoning and success in formal maths. The better one’s approximate number sense, it seems, the higher one’s chance of getting good grades. This might have serious consequences for education. If a flair for estimation fosters mathematical aptitude, maybe maths classes should be less about times tables and more about honing skills at comparing sets of dots.
Stanislas Dehaene is perhaps the leading figure in the cross-disciplinary field of numerical cognition. He started off as a mathematician, and is now a neuroscientist, a professor at the Collège de France and one of the directors of NeuroSpin, a state-of-the-art research institute near Paris. Shortly after he published
The Number Sense
in 1997, he was having lunch in the canteen of Paris’s Science Museum with the Harvard development psychologist Elizabeth Spelke. There they sat down by chance next to Pierre Pica. Pica brought up his experiences with the Munduruku and, after excited discussions, the three decided to collaborate. The chance to study a community that doesn’t have counting was a wonderful opportunity for new research.
Dehaene devised experiments for Pica to take to the Amazon, one of which was very simple: he wanted to know just what they understood by their number words. Back in the rainforest Pica assembled a group of volunteers and showed them varying numbers of dots on a screen, asking them to say aloud the number of dots they saw.
The Munduruku numbers are:
one | |
two | |
three | |
four | |
five | |
When there was one dot on the screen, the Munduruku said
p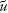 g
g
. When there were two, the said
xep xep
. But beyond two they were not precise. When three dots showed up,
ebapug
was said only about 80 percent of the time. The reaction to four dots was
ebadipdip
in only 70 percent of cases. When shown five dots,
p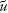 g pogbi
g pogbi
was the answer managed only 28 percent of the time, with
ebadipdip
being given instead in 15 percent of answers. In other words, for three and above the Munduruku’s number words were really just estimates. They were counting ‘one’, ‘two’, ‘threeish’, ‘fourish’, ‘fiveish’. Pica started to wonder whether
p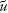 g pogbi
g pogbi
, which literally means ‘handful’, even really qualified as a number. Maybe they could not count up to five, but only to fourish?
Pica also noticed an interesting linguistic feature of their number words. He pointed out to me that from one to four, the number of syllables of each word is equal to the number itself. This observation really excited him. ‘It is as if the syllables are an aural way of counting,’ he said. In the same way that the Romans counted I, II, III and IIII but switched to V at five, the Munduruku started with one syllable for one, added another for two, another for three, another for four but did not use five syllables for five. Even though the words for three and four were not used precisely, they contained precise numbers of syllables. When the number of syllables was no longer important, the word was maybe not a number word at all. ‘This is amazing since it seems to corroborate the idea that humans possess a number system that can only track up to four exact objects at a time,’ Pica said.
Pica also tested the Munduruku’s abilities to estimate large numbers. In one test, illustrated overleaf, the subjects were shown a computer animation of two sets of several dots falling into a can. They were then asked to say if these two sets added together in the can – no longer visible for comparison – amounted to more than a third set of dots that then appeared on the screen. This tested whether they could calculate additions in an approximate way. They could, performing just as well as a group of French adults given the same task.
In a related experiment, also illustrated overleaf, Pica’s computer screen showed an animation of six dots falling into a can and then four dots falling out. The Munduruku were then asked to point at one of three choices for how many dots were left in the can. In other words, what is 6 minus 4? This test was designed to see if the Munduruku understood exact numbers for which they had no words. They could not do the task. When shown the animation of a subtraction that contained either 6, 7 or 8 dots, the solution always eluded them. ‘They could not calculate even in simple cases,’ said Pica.
The results of these dot experiments showed that the Munduruku were very proficient in dealing with rough amounts, but were abysmal in exact numbers above five. Pica was fascinated by the similarities this revealed between the Munduruku and Westerners: both had a fully functioning, exact system for tracking small numbers and an approximate system for large numbers. The significant difference was that the Munduruku had failed to combine these two independent systems together to reach numbers beyond five. Pica said that this must be because keeping the systems separate was more useful. He suggested that in the interests of cultural diversity it was important to try to protect the Munduruku way of counting, since it would surely become threatened by the inevitable increase in contact between the Indians and Brazilian settlers.

