Alex’s Adventures in Numberland (45 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Finding God’s number is extremely complex because the numbers are so large. There are about 43×10
18
(or 43 followed by 18 zeros) cube positions. If every unique cube position were stacked on top of each other, the tower of cubes would go to the sun and back more than eight million times. It would take far too long to analyse each position one by one. Instead, mathematicians have looked at subgroups of positions. Tomas Rokicki, who has been studying the problem for around two decades, has analysed a collection of 19.5 billion related positions and found ways of solving them in 20 moves or less. He has now looked at a million or so similar collections, each containing 19.5 billion positions, and found again that 20 moves was sufficient for a solution. In 2008 he proved that every other remaining Rubik’s Cube position is only two moves away from a position in one of his collections, giving an upper bound for God’s number of 22.
Rokicki is convinced that God’s number is 20. ‘I’ve solved, at this point, approximately 9 percent of all cube positions, and none of them has required 21 moves. If there are any positions that require 21 or more moves, they are exceptionally rare.’ Rokicki’s challenge is not so much theoretical but logistical. Running through sets of cube positions uses an incredible amount of computer memory time. ‘With my current technique, I would need about 1000 modern computers for about one year to prove [that God’s number] is 20,’ he said.
Cube maths has been a long-term hobby for Rokicki. When I asked him whether he has thought of investigating the maths of other puzzles, like Sudoku, he joked: ‘Don’t try to distract me with other shiny problems. Cube math is challenging enough!’
Ernö Rubik still lives in Hungary and rarely gives interviews. I did, however, get a chance to meet one of his former students, Dániel Erdély, in Atlanta. We met in a room in the hotel devoted to ‘mathematical objects’. Origami models, geometrical shapes and elaborate puzzles were laid out on tables. Erdély was there looking after his own creations: light blue objects about the size of cricket balls, ridged with intricate, swirling patterns. Erdély treated them with the affection that a dog breeder has for a litter of his puppies. He picked one up, pointed to the palm-sized planet’s crystalline landscape and said: ‘Spidrons.’
Erdély, like Rubik, is not a mathematician. Rubik is an architect, and Erdély is a graphic designer who studied graphic design at the Budapest College of Applied Arts, where Rubik was a professor. In 1979 Erdély attended classes given by Rubik. As homework for these classes he devised a new shape made out of a sequence of alternate, and shrinking, equilateral and isosceles triangles. He called the shape a ‘spidron’ because it curved like a spiral. By the time he left university, spidrons were his obsession. He played around with them endlessly, noticing that they could fit together like tiles in many aesthetically satisfying ways, in both two and three dimensions. About five years ago, a Hungarian friend helped write a program to generate spidrons on the computer. Their tessellating properties have subsequently captivated mathematicians, engineers and sculptors, and Erdély has made himself the shape’s globetrotting chaperon. He believes it could have applications in the design, for example, of solar panels. At the G4G he had met a man who runs a company that launches rockets. The spidron, he told me, may be about to go into space.
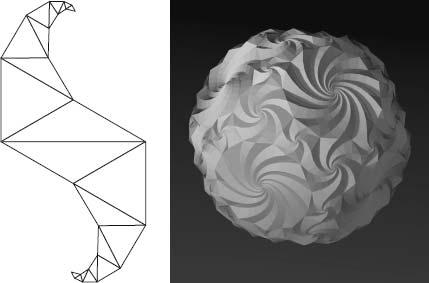
Spidron and spidron ball.
One afternoon the delegates of the conference relocated to the home of Tom Rodgers in the Atlanta suburbs. Rodgers, a businessman in late middle age, organized the first G4G in 1993. An admirer of Gardner’s since childhood, Rodgers’ initial idea was to have an event where the famously shy Gardner could meet some of the many readers he had corresponded with. He decided to invite guests from three specific areas of Gardner’s interest – maths, magic and puzzles. The gathering was such a success that a second one was organized in 1996. Gardner showed up to the first two but since then has been too frail to attend. Rodgers lives in a bungalow designed in Japanese style, surrounded by a forest of bamboo, pine and fruit trees that were in blossom when I visited. In the garden several guests were forming teams to build geometrical sculptures out of wood and metal. Others were attempting to solve a bespoke puzzle hunt whose clues were stuck to the house’s outside walls.
Suddenly, the shriek of Princeton University maths professor John Horton Conway grabbed everyone’s attention. Conway had a messy beard, a full head of silvery hair and was wearing a T-shirt with an equation on it. He is one of the most outstanding mathematicians of the last 50 years. He asked for everyone to bring him ten pine cones each so that he could count their spirals. Cone-classifying is a recent hobby of his; he has counted about 5000 of them since he started a few years ago.
Inside the house I met Colin Wright, an Australian who lives in Port Sunlight on the Wirral. With his schoolboyish ginger hair and glasses, he looks just how you might expect a mathematician to look. Wright is a juggler, which ‘seemed like the obvious thing to do after I learned to ride a unicycle’, he said. He also helped develop a mathematical notation for juggling, which might not sound like much, but has electrified the international juggling community. It turns out that with a language, jugglers have been able to discover tricks that had eluded them for thousands of years. ‘Once you have a language to talk about a problem, it aids your thought process,’ said Wright, as he took out some bean balls to demonstrate a recently invented three-ball juggle. ‘Maths is not sums, calculations and formulae. It is pulling things apart to understand how things work.’
I asked him if there was something self-indulgent, pointless or even wasteful about the finest minds in mathematics spending their time working on inconsequential pastimes like juggling, counting pine cones or even puzzle-solving. ‘You need to let mathematicians do what they do,’ he replied. ‘You genuinely never know what is going to be useful.’ He quoted the example of Cambridge professor G.H. Hardy, who in 1940 famously (and proudly) declared that number theory had no practical applications; in fact, it is now the basis of many internet security programs. Mathematicians have, according to Wright, been ‘unreasonably successful’ in finding applications to apparently useless theorems, and often years after the theorems were first discovered.
One of the most charming aspects of the G4G is that all guests are asked to bring a gift – ‘something you would want to give to Martin’. In fact, you are asked to bring 300 of your gift, since each guest is given a goody bag at the end, containing one of everyone else’s gift. The year I visited the goody bag included puzzles, magic tricks, books, CDs, gadgets and piece of plastic that can mke a Coke can talk. One bag was for Martin Gardner, and I took it to him.
Gardner lives in Norman, Oklahoma. The day I arrived storms were moving across the state. After a few wrong turns off the interstate, I found his home, an Assisted Living Center next to a Texan fast-food joint. The door to his room is only a few steps from the entrance, past a common area where a couple of the elderly residents was sitting and chatting. By Gardner’s door was a box of correspondence. He does not use email. He sends more letters than the rest of the home combined.
Gardner opened the door and invited me in. On the wall there was a portrait of him made out of dominoes, a large photograph of Einstein and an Escher original. Gardner was casually dressed in a green shirt and slacks. He had a soft, open complexion, with wisps of white hair, large tortoiseshell glasses and alert eyes. There was an ethereal aspect to him. He was slim and had excellent posture, possibly because he works every day standing up at his desk.
Visiting Gardner felt straight out of
The Wizard of Oz
. I was in the hurricane-strewn Midwest on a quest to meet an elderly magician. It turned out that Dorothy & co were an especially pertinent reference. I had not known this before I met him, but Gardner is a world expert on L. Frank Baum, the writer of
The Wizard of Oz
. Gardner told me that a decade previously he had even written a sequel in which Dorothy and friends go to Manhattan. It was reviewed in serious newspapers, if not very favourably. ‘It is written mainly for Oz fans,’ he said.
I gave him the G4G goody bag and asked how it felt to be the subject of a conference. ‘I am quite honoured, and surprised,’ he replied. ‘I am amazed at how it has grown.’ It quickly became clear that he was not entirely comfortable talking about his illustriousness among mathematicians. ‘I am not a mathematician,’ he said. ‘I am basically a journalist. Beyond calculus I am lost. That was the secret of my column’s success. It took me so long to understand what I was writing about that I knew how to write about it so most readers would understand it.’ When I learned that Gardner was not a proper mathematician I initially felt a little disappointed, as though the Wizard had pulled away the curtain.
Gardner’s preferred subject is magic. He described it as his principal hobby. He subscribes to magic magazines and – as much as his arthritis allows – practises tricks. He offered to show me what he said was the only sleight-of-hand card magic he had invented, called a ‘wink change’, in which the colour of a card is changed ‘in a wink’. He took a pack of cards and lodged a black card between the deck and the palm of his hand. Instantly, the black card became a red one. Gardner became interested in maths through ‘mathematical’ magic tricks, and it was magicians, not mathematicians, who formed his main social circle as a young adult. He said he liked magic because it developed a sense of wonder about the world. ‘You see a woman levitated and that reminds you that it is just as miraculous that she falls to the ground by gravity…you don’t realize that gravity is just as mysterious as a woman levitating.’ I asked him if maths gave him that same wonder. He replied, ‘Absolutely, yes.’
Gardner may be best known for his writings on maths, but they represent only a portion of his output. His first book was
Fads and Fallacies
, the first popular book to debunk pseudoscience. He has written on philosophy and published a serious novel about religion. His bestselling book is pan>
The Annotated Alice
, a timeless compendium of footnotes to
Alice in Wonderland
and
Through the Looking-Glass
. At 93, the output shows no signs of slowing down. He is due to publish a book of essays on G.K. Chesterton, and among his many other projects he is compiling a bumper book of word games.
Thanks to Gardner, recreational mathematics remains in very good shape. It is an exciting and diverse field that continues to give pleasure to people of all ages and nationalities, as well as inspiring serious research on serious problems. I had been slightly disheartened to learn that Gardner was not a mathematician, but as I left the Assisted Living Center, it struck me, after all, that it was brilliantly in the spirit of recreational maths that the man who now personifies it was only ever an enthusiastic amateur.

In Atlanta I met a man with an unusual hobby. Neil Sloane collects numbers. Not individual numbers, that would be silly, but families of numbers in ordered lists called sequences. For example, the natural numbers are a sequence, which can be defined by saying that the
n
th term in the sequence is
n
:
1, 2, 3, 4, 5, 6, 7…
Sloane started his collection in 1963, as a graduate student at Cornell, where he first wrote the sequences on cards. It made perfect sense for someone who liked ordered lists to make an ordered list of them. By 1973 he had reached 2400 sequences, which he published in a book entitled
A Handbook of Integer Sequences
. By the mid nineties he was up to 5500. Only with the invention of the internet, however, did the collection find its ideal medium. Sloane’s list blossomed into the
On-Line Encyclopedia of Integer Sequences
, a compendium that now has more than 160,000 entries, and expands by about 10,000 a year.
On first acquaintance, Sloane appears a typical indoors type. He is slight, bald and wears thick, square glasses. Yet he is also sinewy and tough, carrying himself with a Zen-like poise – a benefit of his other passion, which is rock-climbing. Sloane likes the challenges of ascending geological formations just as much as he likes ascending numerical ones. In Sloane’s opinion, the similarity between studying sequences and rock-climbing is that they both demand shrewd puzzle-solving skills. I’d say there’s another parallel: sequences encourage the number equivalent of mountaineering – whenever you reach term
n
the natural inclination is to find term
n
+ 1. The desire to reach the next term is like the desire to climb higher and higher peaks; although mountaineers, of course, are restricted by geography, while sequences will often carry on for ever and ever.
Like a record collector who stacks the old favourites by the colourful rarities, Sloane embraces the common as well as the bizarre for his
Encyclopedia
. His collection contains, for example, the sequence below, the ‘zero sequence’, which consists of only 0s. (Each sequence in the
Encylopedia. Byn> is given a reference number prefixed by the letter A. The zero sequence was the fourth sequence Sloane collected, and hence is known as A4.)
(A4) 0, 0, 0, 0, 0…
As the simplest-possible unending sequence, it is the least dynamic in the collection, although it does have a certain nihilistic charm.
Maintaining the
On-Line Encyclopedia
is a full-time job for Sloane, which he does in addition to his real job as a mathematician at AT&T Labs in New Jersey. But he no longer needs to spend time rooting around for new sequences. With the
Encyclopedia
’s success, he is constantly receiving submissions. They come from professional mathematicians and, in larger numbers, numerically obsessed lay-people. Sloane has only one criterion for letting a sequence join the club: it must be ‘well defined and interesting’. The former just means that each term in the sequence can be described, either algebraically or rhetorically. The latter is a matter of his judgement, although his tendency is to accept if he’s ever unsure. Being well defined and interesting, however, does not mean there is something mathematical going on. History, folklore and quirkiness are all fair game.
Among the sequences included in the
Encyclopedia
is the ancient sequence:
(A100000) 3, 6, 4, 8, 10, 5, 5, 7
The sequence numbers are the translation into digits of marks made on one of the oldest-known mathematical objects: the Ishango bone, a 22,000-year-old artefact found in what is now the Democratic Republic of the Congo. The monkey bone was initially thought to be a tally stick, but it has since been suggested that the pattern of 3, followed by its double, then 4, followed by its double, then 10, followed by its half, indicates more sophisticated arithmetical reasoning. There’s also a hateful sequence in the collection:
(A51003) 666, 1666, 2666, 3666, 4666, 5666, 6660, 6661…
This sequence is also known as the Beastly numbers, since they are the numbers containing the string 666 in their decimal expansion.
On a lighter note, here’s a nursery sequence:
(A38674) 2, 2, 4, 4, 2, 6, 6, 2, 8, 8, 16
These are the numbers from the Latin American children’s song ‘La Farolera’:
‘Dos y dos son quatro, cuatro y dos son seis. Seis y dos son ocho, y ocho dieciseis.’
But perhaps the most classic sequence of all is the prime numbers:
(A40) 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37…
Prime numbers are the natural numbers greater than 1 that are divisible only by themselves and 1. They are simple to describe but the sequence exhibits some rather spectacular, and sometimes mysterious, qualities. First, as Euclid proved, there is an infinite number of them. Think of a number, any number, and you will always be able to find a prime number higher than that number. Second, every natural number above 1 can be written as a unique product of imes. In other words, every number is equal to a unique set of prime numbers multiplied by each other. For example, 221 is 13×17. The next number, 222, is 2×3×37. The one after that, 223, is prime, so produced only by 223×1, and 224 is 2×2×2×2 × 2 × 7. We could carry on for ever and each number could be winnowed down to a product of primes in only one possible way. For example, a billion is 2×2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5. This characteristic of numbers is known as the
fundamental theorem of arithmetic
, and is why primes are considered the indivisible building blocks of the natural number system.
Primes are also building blocks when we add them together. Every even number bigger than 2 is the sum of two primes:
4 = 2 + 2
6 = 3 + 3
8 = 5 + 3
10 = 5 + 5
12 = 5 + 7
…
222 = 199 + 23
224 = 211 + 13
…
This proposition, that every even number is the sum of two primes, is known as the Goldbach Conjecture, named after the Prussian mathematician Christian Goldbach, who corresponded with Leonhard Euler about it. Euler was ‘entirely certain’ that the conjecture was true. In almost 300 years of looking and trying, no one has found an even number that is
not
the sum of two primes, but so far no one has actually been able to prove that the conjecture is true. It is one of the oldest and most famous unsolved problems in mathematics. In 2000, so confident were they that a proof was still beyond the limits of mathematical knowledge that the publishers of the mathematical detective story
Uncle Petros and Goldbach’s Conjecture
offered a $1,000,000 prize for anyone who could solve it. No one did.
The Goldbach Conjecture is not the only unresolved issue regarding the primes. Another focus of study is how they seem to be scattered unpredictably along the number line, with no obvious pattern to the sequence. In fact, the search for the harmonies that underpin the distribution of the primes is one of the richest areas of enquiry in number theory, and it has led to many deep results and suppositions.
For all their pre-eminence, however, the primes do not have exclusive claim among the sequences to holding special secrets of mathematical order (or disorder). All sequences contribute in some way to a greater appreciation of how numbers behave. Sloane’s
On-Line Encyclopedia of Integer Sequences
can also be considered a compendium of patterns, a Domesday Book of mathematical DNA, a directory of the underlying numerical order of the world. It might have sprung from Neil Sloane’s personal obsession, but the project has become a truly important scientific resource.
Sloane compares the
Encyclopedia
to a maths equivalent of the FBI fingerprint database. ‘When you go to a crime scene and you take a fingerprint, you then check it against the file of fingerprints to identify the suspect,’ he said. ‘It’s the same thing with the
Encyclopedia
. Mathematicians will come up with a sequence of numbers that occurs naturally in their work, and then they look it up in the database – and it’s lovely for them if they find it there already.’ The database’s usefulness is not restricted to pure mathematics. Engineers, chemists, physicists and astronomers have also looked up, and found, sequences in the
Encyclopedia
, making unexpected connections and gaining mathematical insights into their own fields. For anyone who is working in an area that spews out unfathomable number sequences that they hope to make some sense of, the database is a goldmine.
Through the
Encyclopedia
, Sloane sees a lot of new mathematical ideas, and he also spends time inventing his own. In 1973 he came up with the concept of the ‘persistence’ of a number. This is the number of steps that it takes to get to a single digit by multiplying all the digits of the preceding number to obtain a second number, then multiplying all the digits of that number to get a third number, and so on until you get down to a single digit. For example:
88
8 × 8 = 64
6 × 4 = 24
2 × 4 = 8
So, according to Sloane’s system, 88 has persistence 3, since it takes three steps to get to a single digit. It would seem likely that the bigger a number is, the bigger its persistence. For example, 679 has persistence 5:
679
378
168
48
32
6
