Alex’s Adventures in Numberland (40 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos


For further amazement, rotate Dürer’s square by 180 degrees, then subtract 1 from the squares containing 11, 12, 15 and 16. The result is the following:

The image is from the side of the Sagrada Família cathedral in Barcelona, designed by Antoni Gaudí. Gaudí’s square is not magic, as two numbers are repeated, but it is still pretty special. The columns, rows and diagonals now all add up to 33: the age of Christ at his death.
Hours of fun can be had by playing around with magic squares, and marvelling at the patterns and harmonies. In fact, no other area of non-practical maths has attracted as much attention from amateur mathematicians over such a long period. In the eighteenth and nineteenth centuries, literature on magic squares flourished. One of the most notable enthusiasts was Benjamin Franklin, one of the Founding Fathers of the United States who, as a young clerk of the Pennsylvania Assembly, got so bored during debates that he would construct his own squares. His best-known square is the 8 × 8 variation shown opposite, which he is said to have invented as a boy. In this square Franklin included one of his own enhancements to the theory of magic squares: the ‘broken diagonal’, which are the number in the black squares and grey squares, shown in A and B below. While his square isn’t a proper magic square because the full diagonals don’t add up to the number 260, his newly invented broken diagonals do. The sums of the black squares in C and D and E, and the sum of the grey squares in E and, of course, the sum of every row and column, also add up to 260.
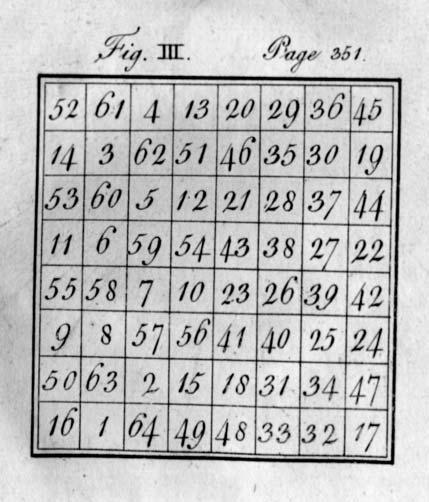
In a letter published in 1769, Benjamin Franklin commented about a book of magic squares: ‘In my younger days…I had amused myself in making these kind of magic squares and, at length, had acquired such a knack at it, that I could fill the cells of any magic square, of reasonable size, with a series of numbers as fast as I could write them, disposed in such a manner, as that the sums of every row, horizontal, perpendicular, or diagonal, should be equal; but not being satisfied with these, which I looked on as common and easy things, I had imposed on myself more difficult tasks, and succeeded in making other magic squares, with a variety of properties, and much more curious.’ He then introduced the square above, printed in his
Experiments and Observations on Electricity, made at Philadelphia in America
, in 1769.
Franklin’s square contains even more beguiling symmetries. The sum of the numbers in every 2 × 2 subsquare is 130, as is the sum of any four numbers that are arranged equidistant from the centre. Franklin is also said to have invented another square in his forties. Over the course of a single evening, he composed an incredible 16 × 16 square that he claimed was ‘the most magically magical of any magic square ever made by any magician’. (It is in the
appendices
.)
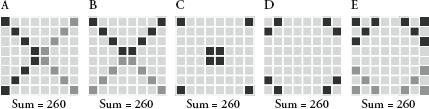
One of the reasons for the enduring popularity of constructing magic squares is that there is a surprising number of them. Let’s count them, starting from the smallest: there is just one magic square in a 1 × 1 grid: the number 1. There are no magic squares with four numbers in a 2 × 2 grid. There are eight ways to arrange the digits 1 to 9 so that the resulting 3 × 3 square is magic, but each of these eight squares is really the same square either rotated or reflected, so it’s conventional to say that there is only one true 3 × 3 magic square. The figure on the opposite page shows how to generate each possibility, starting with the
lo shu
.
Amazingly, after three, the number of magic squares that can be made grows staggeringly fast. Even after reducing the number by ignoring rotations and reflections, it is possible to make 880 magic squares in a 4 × 4 grid. In a 5 × 5 grid the number of magic squares is 275,305,224, a result calculated in 1973, and only through the use of a computer. And though this number seems astronomically high, it is, in fact, tiny compared to the number of all possible arrangements of the digits 1 to 25 in a 5 × 5 square. The total number of arrangements is calculated by multiplying 25 by 24 by 23 and so on until 1, which is about 1.5 followed by 25 zeros, or 15 septillions.
The number of 6 × 6 magic squares is not even known, although it is likely to be in the order of 1 followed by 19 zeros. The number is so huge that it exceeds even the total number of grains of wheat in the chessboard exampe on chapter 6.
Magic squares have not been just the province of amateurs. At the end of his life, the eighteenth-century Swiss mathematician Leonhard Euler became curious about them. (He was almost totally blind by this time, which makes his research into what is an essentially spatial application of numbers especially awe-inspiring.) In particular, his work included the study of a modified version in which each number or symbol in the grid appears exactly once in each row and column. He called it a Latin square.

Latin squares.
Unlike magic squares, Latin squares have several practical applications. They can be used to work out brackets in round-robin sports tournaments, in which every team has to play every other team, and in agriculture they form a handy grid that enables a farmer to test, for example, several different fertilizers on a piece of land to see which works best. If the farmer has, say, six products to test and he divides the land into a 6 × 6 square, distributing each product in the pattern of a Latin square ensures that any change in soil conditions affects each treatment equally.
Maki Kaji, the Japanese puzzle-maker I introduced at the start of the chapter, ushered in a new era of number-square fascination. The idea came to him as he was browsing an American puzzle magazine. As a non-English-speaker, he scanned pages of incomprehensible word games before stopping when he came across an intriguing-looking grid of numbers. The puzzle, entitled ‘Number Place’, was a partially completed 9 × 9 Latin square that used the digits 1 to 9. Based on the rules that each number was allowed to appear only once per row and per column, the would-be solver needed to figure out how to fill in the missing gaps using a process of logical deduction. Solvers were aided by a further condition: the square was divided into nine 3 × 3 subsquares, each of which was marked in bold. Each number 1–9 was allowed only once per subsquare. Kaji solved Number Place and got excited – this was precisely the sort of puzzle he wanted to put in his new magazine.
Number Place, which had made its first appearance in 1979, was the creation of Howard Garns, a retired architect and puzzle enthusiast from Indiana. Though he enjoyed solving Garns’s puzzle, Kaji decided to redesign it so that the numbers provided were distributed in a symmetrical pattern around the grid, matching the format used for crosswords. He called his version Sudoku, the Japanese for ‘the number must appear only once’.
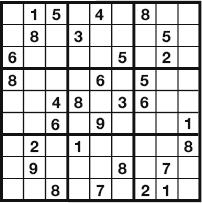
Sudoku appeared in the early issues of Kaji’s puzzle magazine, which launched in 1980, but Kaji said it attracted no attention. It was only once the puzzle travelled overseas that it spread like wildfire.
Just as a Japanese-speaker with no English could understand Number Place, so an English-speaker with no Japanese could understand Sudoku. In 1997 a New Zealander named Wayne Gould walked into a bookstore in Tokyo. Although he was initially disoriented by the fact that everything was in Japanese, his eyes eventually landed on something familiar. He saw a book cover with what looked like a crossword grid with numbers on it, and though the image was obviously some kind of puzzle, he didn’t instantly understand the rules. Stll, he bought the book, thinking he’d figure it out later. On a holiday in southern Italy he worked backwards until he cracked the puzzle. Gould had just retired from being a judge in Hong Kong and was teaching himself how to program computers, so he decided he would try to write a program that generated Sudokus. A top programmer might take a couple of days for this task. It took Gould six years.
