Alex’s Adventures in Numberland (62 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Blackjack, or twenty-one, is a card game in which the aim is to get a hand where the total value of the cards is as close as possible to an upper limit of 21. The dealer also deals a hand for himself. To win, you must have a hand higher than his while not exceeding 21.
Like all the classic casino games, blackjack gives a slight advantage to the house. If you play blackjack, in the long run you will lose money. In 1956 an article was published in an obscure statistics journal that claimed to have devised a playing strategy that gave the house an advantage of just 0.62 percent. After reading the article, Thorp learned the strategy and tested it during a vacation trip to Vegas. He discovered that he lost his money much slower than the other players. He decided he would begin to think deeply about blackjack, a decision that would change his life.
Ed Thorp is now 75 but I suspect he doesn’t look that different from how he looked half a century ago. Slim, with a long neck and concise features, he has a clean-cut college-boy haircut, unpretentious glasses, and a calm, upright posture. After returning from Vegas, Thorp reread the journal article. ‘I saw right away, within a couple of minutes, how you could almost certainly beat this game by keeping track of the cards that were played,’ he remembered. Blackjack is different from, say, roulette, since the odds change once a card has been dealt. The chance of getting a 7 in roulette is 1 in 38 every time you spin the wheel. In blackjack the probability>
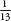 13. If the first dealt card is an ace, the probability of the second card being an ace, however, is not
13. If the first dealt card is an ace, the probability of the second card being an ace, however, is not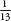 – it is
– it is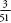 , since the pack now has 51 cards and there are only 3 aces left in it. Thorp thought there must be a system that turned the odds in the favour of the player. It then became just a matter of finding it.
, since the pack now has 51 cards and there are only 3 aces left in it. Thorp thought there must be a system that turned the odds in the favour of the player. It then became just a matter of finding it.
In a 52-card deck there are 52×51×50×49×…×3×2×1 ways of the cards being ordered. This number is about 8×10
67
, or 8 followed by 67 zeros. The number is so huge that it is very unlikely that any two randomly shuffled decks will ever have had the same order in the history of the world – even if the world’s population had started playing cards at the Big Bang. Thorp reasoned that there are too many possible permutations of cards for any system of memorizing permutations to be feasible for a human brain. Instead he decided to look at how the house advantage changes depending on which cards have already been dealt. Using a very early computer, he found that by keeping track of the number-five cards of each suit – the five of hearts, spades, diamonds and clubs – a player could judge whether the deck was favourable. Under Thorp’s system, blackjack morphed into a beatable game, with an expected return of up to 5 percent depending on the cards left in the pack. Thorp had invented ‘card-counting’.
He wrote up his theory and submitted it to the American Mathematical Society (AMS). ‘When the abstract came through everybody thought it was ridiculous,’ he remembered. ‘It was gospel in the scientific world that you couldn’t beat any of the major gambling games, and that had rather strong support from the research and analysis that had been done over a couple of centuries.’ Proofs that demonstrate that you can beat the odds at casino games are rather like proofs that you can square the circle – surefire evidence of a crackpot. Luckily, one of the members of the AMS’s submission committee was an old classmate of Thorp’s, and the abstract was accepted.
In January 1961 Thorp presented his paper at the American Mathematical Society’s winter meeting in Washington. It made national news, including the front page of his local paper, the
Boston Globe
. Thorp received hundreds of letters and calls, with many offers to finance gambling sprees for a share of the profit. A syndicate from New York was offering $100,000. He called the number on the New York letter and the following month a Cadillac pulled up outside his apartment. Out stepped a pint-sized senior citizen, accompanied by two spectacular blondes in mink coats.
The man was Manny Kimmel, a mathematically astute New York gangster and inveterate high-stakes gambler. Kimmel had taught himself enough about probability to know the birthday paradox – one of his favourite things to bet on was whether two people in a group shared the same birthday. Kimmel introduced himself as the owner of 64 parking lots in New York City, which was true. He introduced the girls as his nieces, which probably wasn’t. I asked Thorp if he suspected Kimmel of mob ties. ‘At that time I wasn’t very knowledgeable about the gambling world; in fact I had no knowledge of it except the theoretical, and I also hadn’t investigated the world of crime. He represented himself as a wealthy businessman and the evidence for that was overwhelming.’ Kimmel invited Thorp to play blackjack at his luxurious Manhattan apartment the following we. After a few sessions, Kimmel was convinced that card-counting worked. Both men flew to Reno to try it out. They started off with $10,000 and by the end of the trip had built their pot up to $21,000.
When you are gambling in a casino, two factors come into play that determine how much money you will win or lose.
Playing strategy
is about how to win a game.
Betting strategy
is about money management – how much to bet and when. Is it worth, for example, betting your entire purse on one bet? Or is it worth dividing your money up into the smallest possible stakes? Different strategies can have a surprisingly large impact on how much money you can expect to make.
The best-known betting strategy is called the ‘martingale’, or doubling up, and was popular with French gamblers in the eighteenth century. The principle is to double your bet if you lose. Let’s say you are betting on the toss of a coin. Heads you win $1, tails you lose $1. Just say the first flip is tails. You lose $1. For the next bet you must stake $2. Winning on the second bet wins you $2, which recoups your $1 loss from the first bet and puts you $1 in profit. Say you lose the first five flips:
Lose $1 bet so next time bet $2
Lose $2 bet so next time bet $4
Lose $4 bet so next time bet £8
Lose $8 bet so next time bet $16
Lose $16 bet
You will be 1 + 2 + 4 + 8 + 16 = $31 down, so the sixth bet must be for $32. If you win you recoup your losses, and profit. But despite risking so much money, you are only ahead by $1, your original stake.
Martingale certainly has an appeal. In a game where the odds are almost 50:50 – like, say, betting on the red at roulette, which has a probability of 47 percent – you are very likely to win a fair percentage of plays and so have a good chance of staying ahead. But the martingale system is not fail-safe. For a start, you are only winning in small increments. And we know that in a run of 30 coin flips, a streak of five heads, or five tails, is more likely than not. If you start with a $40 bet and have a five-game losing streak, you will find yourself having to bet $1280. At the Peppermill Casino, though, you wouldn’t be able to – it has a maximum bet of $1000. One reason why casinos have maximum bets is to stop systems like martingale. The exponential growth of martingale bets on a losing streak often accelerates bankruptcy, rather than insuring against it. The system’s most famous champion, eighteenth-century Venetian playboy Giacomo Casanova, discovered this the hard way. ‘I still played on the martingale,’ he once said, ‘but with such bad luck that I was soon left without a sequin.’
Still, if you stood at the Peppermill roulette table playing martingale with a $10 starting stake on red, you would have to be very unlucky not to eventually win $10. The system would break down only if you lost six times in a row, and there is only a 1-in-47 chance of that happening. Once you have won, however, it would then be advisable to cash in your winnings and leave. By continuing to gamble, the chances of an unlucky streak will eventually become more likely than not.
Let’s consider a different system of betting. Imagine you are given $20,000 in a casino and told you must gamble it on red roulette table. What’s the best strategy for doubling your money? Is to be bold and bet the whole thing in one bet, or to be cautious and bet in the smallest possible amount, in stakes of $1? Even though it seems initially reckless, your chances of success are much better if you bet the whole amount in one go. In maths-speak, bold play is
optimal
. With a smidgen of reflection, this makes sense: the law of large numbers says that you will lose in the long run. Your best chances are to make the run as short as possible.
In fact, this is exactly what Ashley Revell, a 32-year-old from Kent, did in 2004. He sold all his possessions, including his clothes, and in a Las Vegas casino bet the total amount – $135,300 – on red. Had he lost, he would have at least become a C-list TV celebrity, as the bet was being filmed for a TV reality show. But the ball landed on red 7, and he came home with $270,600.
At blackjack, Ed Thorp was presented with a different issue. His card-counting system meant that he could tell at certain points during the game whether he had an advantage over the dealer. Thorp asked himself: what is the best betting strategy when the odds are in your favour?
Imagine there is a bet where the chance of winning is 55 percent and the chance of losing 45 percent. For simplicity, the game pays evens and we play it 500 times. The advantage – the
edge
– is 10 per cent. In the long run our winnings will work out on average as a $10 profit for every $100 gambled. To maximize our total profit, we obviously need to maximize the combined total of wagers. It is not immediately obvious how this is done, since maximizing wealth requires a minimizing of the risk of losing it all. This is how four betting strategies perform:
Strategy 1: Bet everything
. Just like Ashley Revell, put your entire bankroll on the first bet. If you win, you have doubled your money. If you lose, you are bankrupt. If you win, put everything down again for the next bet. The only way you can avoid losing everything is if you win all 500 games. The chance of this happening, if the probability of winning each game is 0.55, is about one in 10
130
, or 1 followed by 130 zeros. In other words, it is almost certain you will be bankrupt by the 500th game. Obviously, this is
not
a good long-term strategy.
Stategy 2: Fixed wager
. Bet a fixed amount on every bet. If you win, your wealth grows by that fixed amount. If you lose, your wealth shrinks by that amount. Since you win more than you lose, your wealth will increase overall, but it does so only by increasing in jumps of the same fixed amount. As the graph overleaf shows, your money doesn’t grow very fast.
Strategy 3: Martingale
. This gives a faster rate than fixed wager, since losses are compensated by doubling up after a loss, but brings with it a much higher risk. With only a few losing bets, you could be bankrupt. Again, this is
not
a good long-term strategy.
