Alex’s Adventures in Numberland (57 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

The expected outcome becomes an eternity in Hell, which looks like a terrible bet. Again, if the chance of God existing is only a hundredth, the equation is similarly bleak for non-believers. If there is any chance at all of God existing, for the non-believer the expected value of the gamble is always infinitely bad.
The above argument is known as Pascal’s Wager. It can be summarized as follows: if there is the slightest probability that God exists, it is overwhelmingly worthwhile to beliee in Him. This is because if God doesn’t exist a non-believer has nothing to lose, but if He does exist a non-believer has
everything
to lose. It’s a no-brainer. Be a Christian, go on, you might as well.
Upon closer examination, though, Pascal’s argument, of course, doesn’t work. For a start, he is only considering the option of believing in a Christian God. What about the gods of any other religion, or even of made-up religions? Imagine that, in the afterlife, a cat made of green cheese will determine whether we go to Heaven or Hell. Although this isn’t very likely, it’s still a possibility. By Pascal’s argument, it is worthwhile to believe that this cat made from green cheese exists, which is, of course, absurd.
There are other problems with Pascal’s Wager that are more instructive to the mathematics of probability. When we say that there is a 1-in-6 chance of a die landing on a six, we do this because we know that there is a six marked on the die. For us to be able to understand in mathematical terms the statement that there is a 1 in anything chance of God existing, there must be a possible world where God does in fact exist. In other words, the premise of the argument presupposes that, somewhere, God exists. Not only would a non-believer refuse to accept this premise, but it shows that Pascal’s thinking is self-servingly circular.
Despite Pascal’s devout intentions, his legacy is less sacred than it is profane. Expected value is the core concept of the hugely profitable gambling industry. Some historians also attribute to Pascal the invention of the roulette wheel. Whether this is true or not, the wheel was certainly of French origin, and by the end of the eighteenth century roulette was a popular attraction in Paris. The rules are as follows: a ball spins around an outer rim before losing momentum and falling towards an inner wheel, which is also rotating. The inner wheel has 38 pockets, marked by the numbers 1 to 36 (alternately red and black) and the special spots 0 and 00 (green). The ball reaches the wheel and bounces around before coming to rest in an individual pocket. Players can make many bets on the outcome. The simplest is to bet on the pocket where the ball will land. If you get it correct, the house pays you back 35 to 1. A £10 bet, therefore, wins you £350 (and the return of your £10 bet).
Roulette is a very efficient money-making machine because every bet in roulette has a negative expected value. In other words, for every gamble you make you can expect to lose money. Sometimes you win and sometimes you lose, but in the long run you will end up with less money than you started with. So, the important question is, how much can you expect to lose? When you bet on a single number, the probability of winning is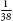 , as there are 38 potential outcomes. For each single number bet of £10, therefore, a player can expect to win:
, as there are 38 potential outcomes. For each single number bet of £10, therefore, a player can expect to win:
(chance of landing on a number)(what you win) + (chance of not landing on a number)(what you win)
or
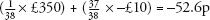
In other words, you lose 52.6p for every £10 wagered. The other bets in roulette – betting on two or more numbers, on sections, colours, or columns, all have odds that result in an expected value of –52.6p, apart from the ‘fnumber’ bet on getting either 0, 00, 1, 2 or 3, which has even worse odds, with an expected loss of 78.9p.
Despite its bad odds, roulette was – and continues to be – a much-loved recreation. For many people, 52.6p is a fair payment for the thrill of potentially winning £350. In the nineteenth century casinos proliferated and, in order to make them more competitive, roulette wheels were built without the 00, making the chance of a single-number bet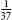 and reducing the expected loss to 27p per £10 bet. The change meant that you lost your money about half as quickly. European casinos tend to have wheels with just the 0, while America prefers the original style, with 0 and 00.
and reducing the expected loss to 27p per £10 bet. The change meant that you lost your money about half as quickly. European casinos tend to have wheels with just the 0, while America prefers the original style, with 0 and 00.
All casino games involve negative-expectation bets; in other words, in these games gamblers should expect to lose money. If they were arranged in any other way, casinos would go bust. Mistakes, however, have been made. An Illinois riverboat casino once introduced a promotion that changed the amount paid out on one type of hand in blackjack without realizing that the change moved the expected value of the bet from negative to positive. Instead of expecting to lose, gamblers could expect to win 20 cents per $10 bet. The casino reportedly lost $200,000 in a day.
The best deal to be found in a casino is at the craps table. The game originated from a French variant of an English dice-rolling game. Players throw two dice and the outcome depends on which numbers land and how they add up. In craps, your chances of winning are 244 out of 495 possible outcomes, or 49.2929 percent, giving an expected loss of just 14.1p per £10 bet.
Craps is also worth mentioning because of the possibility of making a curious side bet in which you can bet with the house; that is, against the player throwing the dice. The side bettor wins when the main bettor loses, and the side bettor loses when the main bettor wins. Since the main bettor loses, on average, 14.1p per £10 bet, the side bettor stands to win, on average, 14.1p per £10 bet. But there is an extra rule preventing this neat outcome in craps side bets. If the main player rolls a double six on his first roll (which means that he loses), the side bettor does not win either, but only receives his money back. This seems like a very insignificant change. There’s only a 1-in-36 chance of throwing a double six. Yet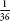 less of a chance of winning decreases the expected value by 27.8p per £10 bet, which shifts the expected value of the bet into negative territory. Instead of winning 14.1p per £10 as the house does, the side bettor will win 14.1p minus 27.8p per bet, which is –13.7p, or a loss of 13.7p. The side bet is indeed a better deal, but only marginally, by 0.4p per £10 wagered.
less of a chance of winning decreases the expected value by 27.8p per £10 bet, which shifts the expected value of the bet into negative territory. Instead of winning 14.1p per £10 as the house does, the side bettor will win 14.1p minus 27.8p per bet, which is –13.7p, or a loss of 13.7p. The side bet is indeed a better deal, but only marginally, by 0.4p per £10 wagered.
Another way of looking at an expected loss is to consider it in terms of
payback percentage
. If you bet £10 at craps, you can expect to receive about £9.86 back. In other words, craps has a payback percentage of 98.6 percent. European roulette has a payback percentage of 97.3 percent; and US roulette, 94.7 percent. While this might seem a bad deal to gamblers, it is better value than the slots.
In 1893 the
San Francisco Chronicle
notified its readers that the city was home to one and a half thousand ‘Nickel-in-the-Slot Machines That Make Enormous Profits…They are of mushroom growth, having appeared in the space of only a few months.’ The machines came in many styles, but it was only at the turn of the century, when Charles Feya German immigrant, came up with the idea of three spinning reels, that the modern-day slot machine was born. The reels of his Liberty Bell machine were marked with a horseshoe, a star, a heart, a diamond, a spade, and an image of Philadelphia’s cracked Liberty Bell. Different combinations of symbols gave different payouts, with the jackpot set to three bells. The slot machine added an element of suspense its competitors did not have because, when spun, the wheels came to rest one by one. Other companies copied, the machines spread beyond San Francisco, and by the 1930s three-reel slots were part of the fabric of American society. One early machine paid out fruit-flavoured chewing gum as a way to get round gaming laws. This introduced the classic melon and cherry symbols and is why slots are known in the UK as fruit machines.
The Liberty Bell had a payback average of 75 percent, but these days slots are more generous than they used to be. ‘The rule of thumb is, if it’s a dollar denomination [machine], most people would put [the payback percentage] at 95 percent,’ said Anthony Baerlocher, the director of game design at International Game Technology (IGT), a slot-machine company that accounts for 60 percent of the world’s million or so active machines, referring to slots where the bets are made in dollars. ‘If it’s a nickel it’s more like 90 percent, 92 percent for a quarter, and if they do pennies it might go down to 88 percent.’ Computer technology allows machines to accept bets of multiple denominations, so the same machine can have different payback percentages according to the size of the bet. I asked him if there was a cut-off percentage below which players will stop using the machine because they are losing too much. ‘My personal belief is that once we start getting down around 85 percent it’s extremely difficult to design a game that’s fun to play. You have to get really lucky. There’s just not enough money to give back to the player to make it exciting. We can do a pretty good job at 87.5 percent, 88 percent. And when we start doing 95, 97 percent games they can get pretty exciting.’

The size of a cash register, Charles Fey’s Liberty Bell was an immediate success when it was first manufactured at the very end of the nineteenth century.
