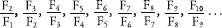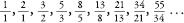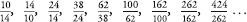Alex’s Adventures in Numberland (52 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

There are many examples in nature of Fibonacci numbers, and one of my favourites concerns the reproductive patterns of bees. A male bee, or drone, has just one parent: his mother. Female bees, however, have two parents: a mother and a father. So, a drone has three grandparents, five great-grandparents, eight great-grandparents, and so on. Plotting a chart of the drone’s ancestry (as in the diagram overleaf), we find that the number of relatives he has per generation is always a Fibonacci number.
In addition to its association with fruit, promiscuous rodents and flying insects, the Fibonacci sequence has many absorbing mathematical properties. Listing the first 20 numbers will help us see the patterns. Each Fibonacci number is traditionally written using an F with a subscript to denote the position of that number in the sequence:
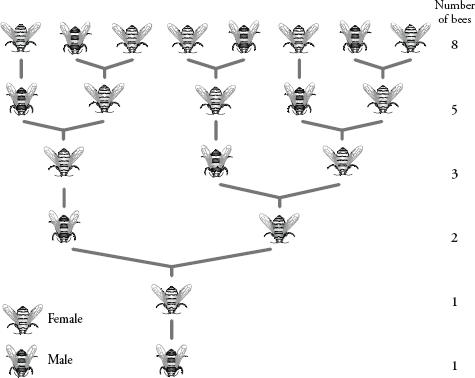
A chart tracing the ancestral history of one male bee (shown at the bottom).
(F0 | 0) |
F1 | 1 |
F2 | 1 |
F3 | 2 |
F4 | 3 |
F5 | 5 |
F6 | 8 |
F7 | 13 |
F8 | 21 |
F9 | 34 |
F | 55 |
F11 | 89 |
F12 | 144 |
F13 | 233 |
F14 | 377 |
F15 | 610 |
F16 | 987 |
F17 | 1597 |
F18 | 2584 |
F19 | 4181 |
F20 | 6765 |
Upon closer examination, we see that the sequence regenerates itself in many surprising ways. Look at F
3
, F
6
, F
9
,…, in other words, every third F-number. They are all divisible by 2. Compare this with F
4
, F
8
, F
12
,…, or every fourth F-number – they are all divisible by 3. Every fifth F-number is divisible by 5; every sixth F-number, divisible by 8; and every seventh number by 13. The divisors are precisely the F-numbers in sequence.
Another amazing example comes from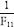 , or
, or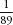 . This number is equal to the sum of:
. This number is equal to the sum of:
.0
.01
.001
.0002
.000005
.0000008
.00000013
.000000021
.0000000034
.00000000055
.000000000089
.0000000000144
So, the Fibonacci sequence pops its head up again.
Here’s another interesting mathematical property of the sequence. Take any three consecutive F-numbers. The first one multiplied by the third one is always one different from the second one squared:
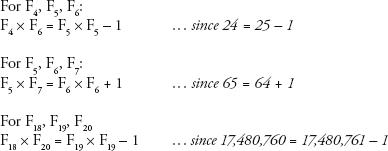
This property is the basis of a centuries-old magic trick, in which it is possible to cut up a square of 64 unit squares into four pieces and reassemble them to make a square of 65 pieces. Here’s how it’s done: draw a square of 64 unit squares. It has a side length of 8. In the sequence, the two F-numbers preceding 8 are 5 and 3. Divide the square up using the lengths of 5 and 3, as in the first image below. The pieces can be reassembled to make a rectangle with sides the length of 5 and 13, which has an area of 65.

The trick is explained by the fact that the shapes are not a perfect fit. Though it is not that obvious to the naked eye, there is a long thin gap along the middle diagonal with an area of one unit.
It follows that a square of 169 unit squares (13 × 13) can be rearranged to ‘make’ a rectangle of 168 squares (8 × 21). In this case the segments overlap slightly along the middle diagonal.
In the early seventeenth century, the German astronomer Johannes Kepler wrote that: ‘As 5 is to 8, so 8 is to 13, approximately, and as 8 to 13, so 13 is to 21, approximately.’ In other words, he noticed that the ratios of consecutive F-numbers were similar. A century later the Scottish mathematician Robert Simson saw something even more incredible. If you take the ratios of consecutive F-numbers and put them in the sequence:
which is:
or (to three decimal places):
1, 2, 1.5, 1.667, 1.6, 1.625, 1.615, 1.619, 1.618…
then the values of these terms get closer and closer to phi, the golden ratio.
In other words, the golden ratio is approximated by the ratio of consecutive Fibonacci numbers, with the approximation increasing in accuracy further down the sequence.
Now let’s continue with this line of thought and consider a Fibonacci-like sequence, starting with two random numbers, and then adding consecutive terms to continue the sequence. So, just say we start with 4 and 10, the following term will be 14 and the one after that 24. Our example gives us:
4, 10, 14, 24, 38, 62, 100, 162, 262, 424…
Look at the ratios of consecutive terms:
The Fibonacci recurrence algorithm of adding two consecutive terms in a sequence to make the next one is so powerful that
whatever
two numbers you start with, the ratio of consecutive terms always converges to phi. I find this a totally enthralling mathematical phenomenon.
The ubiquity of Fibonacci numbers in nature means that phi is also ever present in the world. Which brings us back to the retired dentist, Eddy Levin. Early in his career he spent a lot of time making false teeth, which he found a very frustrating job because no matter how he arranged the teeth he could not make a person’s smile look right. ‘I sweated blood and tears,’ he said. ‘Whatever I did the teeth looked artificial.’ But at around that time Levin started attending a maths and spirituality class, where he learned about phi. Levin was made aware of Pacioli’s
The Divine Proportion
and was inspired. What if phi, which Pacioli claimed revealed true beauty, also held the secret of divine dentures? ‘It was a Eureka moment,’ he said. It was 2 a.m. and he rushed to his study. ‘I spent the rest of the night measuring teeth.’