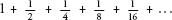Alex’s Adventures in Numberland (49 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Like this one, all of Zeno’s paradoxes draw apparently absurd conclusions by dissecting continuous motion into discrete events. Before Achilles can reach the tortoise, he must complete an infinite number of these discrete dashes. The paradox stems from the assumption that it is impossible to complete an infinite number of dashes in a finite amount of time.
The Greeks, though, didn’t have the depth of mathematical understanding of infinity to see that this assumption is a fallacy. It
is
possible to complete an infinite number of dashes in a finite amount of time. The crucial requirement is that the dashes are getting shorter and taking less time, and that both distance and time are approaching zero. Although this is a necessary condition, it’s not sufficient; the dashes also need to be shrinking at a fast enough rate.
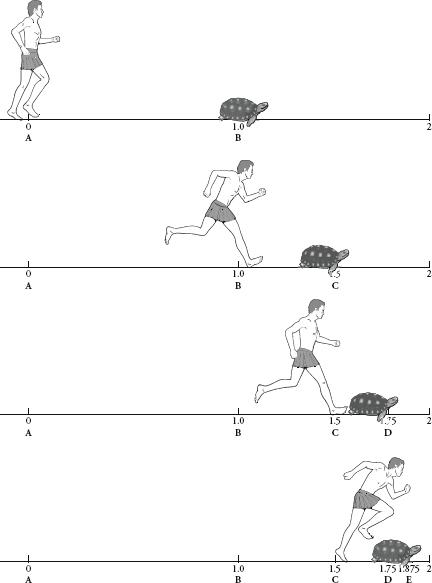
Achilles and the tortoise.
This is what is happening with Achilles and the tortoise. For example, say that Achilles is running at twice the speed of the tortoise and that B is 1m ahead of A. When Achilles reaches B, the turtle has moved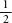 m to C. When Achilles reaches C, the turtle has moved another
m to C. When Achilles reaches C, the turtle has moved another m to D. And so on. The total distance in metres that Achilles is running before he reaches the tortoise is:
m to D. And so on. The total distance in metres that Achilles is running before he reaches the tortoise is:
If it takes Achilles one second to complete each of these intervals then it will take him for ever to complete the distance. But this is not the case. Assuming constant speed, it will take him a second to go a metre, it will take half a second to go half a metre, a quarter of a second to go quarter of a metre, and so on. So, the time in seconds it takes him to reach the tortoise is described by the same addition:
When both time and distance are described by the halving sequence they simultaneously converge at a fixed, finite value. In the above case, at 2 seconds and 2 metres. So, it turns out that Achilles can overtake the tortoise after all.
Not all of Zeno’s paradoxes, however, are solved by the maths of infinite series. In the ‘dichotomy paradox’ a runner is going from A to B. In this case, we’ll call the first point that the runner passes after leaving A point C. For the runner to get to C, however, he must have passed the point that is halfway to C. So C cannot be the first point he passes. It follows that there can be no ‘first point’ that the runner passes, since there will always be a point that he must pass before it. If there is no first point that the runner passes, Zeno argued, the runner cannot ever leave A.
According to lore, to refute this paradox Diogenes the Cynic silently stood up and walked from A to B, thereby demonstrating that such motion was possible. But Zeno’s dichotomy paradox cannot be dismissed so easily. In two and a half thousand years of scholarly head-scratching, no one has been able to solve the riddle totally. Part of the confusion is that a continuous line is not perfectly represented by a sequence of an infinite number of points, or an infinite number of smll intervals. Likewise, the unbroken passage of time is not perfectly represented by an infinite number of discrete moments. The concepts of continuity and discreteness are not entirely reconcilable.
The decimal system throws up an excellent example of a Zeno-inspired paradox. What is the largest number less than 1? It is not 0.9, since 0.99 is larger and still less than 1. It is not 0.99 since 0.999 is larger still and also less than 1. The only possible candidate is the recurring decimal 0.9999…where the ‘…’ means that the nines go on for ever. Yet this is where we come to the paradox. It cannot be 0.9999…since the number 0.9999…is identical to 1!
Think of it this way. If 0.9999…is a different number from 1, then there must be space between them on the number line. So it must be possible to squeeze a number in the gap that is larger than 0.9999…and smaller than 1. Yet what number could this be? You cannot get closer to 1 than 0.9999…. So, if 0.9999…and 1 cannot be different, they must be the same. Counter-intuitive though it is, 0.9999…= 1.
So what is the largest number less than one? The only satisfactory conclusion to the paradox is that the largest number less than 1
doesn’t exist
. (Likewise, there is no largest number less than 2, or less than 3, or indeed less than any number at all.)
The paradox of Achilles’ race against the tortoise was resolved by writing the durations of his dashes as a sum with an infinite amount of terms, which is also known as an infinite series. Whenever the terms of a sequence are added together it is called a
series
. There are both finite and infinite series. For example, if you add up the sequence of the first five natural numbers, you get the finite series:
1 + 2 + 3 + 4 + 5 = 15
Obviously we can work out this sum in our heads, but when a series has many more terms, the challenge is to find a shortcut. One famous example was worked out by the German mathematician Carl Friedrich Gauss when he was a young boy. As the story goes, a schoolteacher is said to have asked him to calculate the sum of the series of the first hundred natural numbers:
1 + 2 + 3 +…+ 98 + 99 + 100
To the teacher’s disbelief, Gauss replied almost instantly: ‘5050.’ The prodigy had worked out the following formula. If you pair off numbers judiciously, by taking the first with the last, the second with the second-last, and so on, then the series can be rewritten as:
(1 + 100) + (2 + 99) + (3 + 98) +…+ (50 + 51)
which is:
101 + 101 + 101 + 101 +…+ 101
There are fifty terms, each with a value 101, so the sum is 50×101 = 5050. We can generalize this to get the result that for any number
n
, the sum of the first
n
numbers is
n
+ 1 added times in a row, which is
times in a row, which is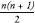 . In the above case
. In the above case
n
is 100, so the sum s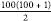 = 5050.
= 5050.
When you add up the terms in a finite series you always get a finite number, that’s obvious. However, when you add up the terms of an infinite series there are two possible scenarios. The
limit
, which is the number that the sum approaches as more and more terms are added, is either a finite number or it is infinite. If the limit is finite, the series is called
convergent
. If not, the series is called
divergent
.