All of the Above (15 page)

“I don't know how his daddy afforded to buy a suit like that,” Sharice whispers to me.
I can see Marcel's father standing near the doorway of the classroom looking proud, as all of the cameras get ready to show Marcel putting the last red tetrahedron on the top. Mr. Collins helps him add the glue to the piece, he reaches toward the top, and then his hand freezes in midair.
“Just a minute,” he says, relaxing his arm and giving his movie-star smile for all the cameras. “I'm not quite ready.”
After a minute or so, he raises his arm again, turns to smile at the cameras, and puts the last tetrahedron, number 16,384, at the top. “This one's for James Harris III,” he says, and all the cameras flash like spotlights.
What's taking them so long? Every day for two weeks, I walk down to the convenience store on the corner, buy a paper, open it up, and look for a picture, and then feel like a fool when nothing is there.
“You looking for somebody you know?” the old store manager asks me.
“Some friends,” I tell him, and each day, he waits until I page through the whole paper piece by piece, even the sports section, before he says, “Not there today?”
“Nope.”
“Maybe tomorrow,” he always answers, and then he pushes a peppermint candy or a piece of chocolate or something across the counter toward me. “Here—consolation prize,” he says, and after two weeks, I get the feeling that he's starting to think I'm just coming in the store for the consolation prize. When I walk through the door, I can see his head shake back and forth a little.
“You know,” he tells me one evening when I stop by, “I've heard that getting in the newspaper isn't all that easy. Too much news to cover these days, and so the reporters have to pick and choose. …”
I tell him that they'll be in the paper.
The old man's head shakes back and forth again.
And then, one Tuesday night, I open up the newspaper and there it is.
“No way,” I say out loud, and the old man slams the cash drawer shut and comes hurrying over from behind the counter to see what I'm looking at. He pulls a paper off the stack and turns to the same page I'm on.
A photograph fills almost half the page. Page 4A. “Students Break Math Record!” the headline says. The photo shows Marcel, who doesn't even look like Marcel, wearing a sharp-looking suit and tie like he's a big star or something. He's standing on a ladder, grinning like a fool, as he's getting ready to put the last tetrahedron on the top.
I squint at the picture, trying to tell if the tetrahedron is red or not. Better be red, Marcel. At the side of the picture, Mr. Collins and Rhondell and Sharice are standing there, watching. Only person missing is me.
But then I see the first sentence at the beginning of the article: “‘This one's for James,’ seventh grader Marcel Williams says, as he proudly puts the final touches on the 16,384-piece tetrahedron built by a group of inner-city kids in Cleveland, Ohio.”
“I'm the James he's talking about here,” I tell the store manager. “Look at that first sentence.” I point at the words. “That's me.”
The store manager's eyes go from the newspaper to me and back again. “You're a math champion?” he asks, like he doesn't quite believe I'm telling the truth.
“That's right.” I nod. “My name is gonna be in the
Guinness Book of World Records
someday.”
The old man sticks out his hand. “Well, let me shake your hand, son,” he says in a formal voice. “I've never met anybody who had a world record before.”
And then he lays the paper on the store counter and carefully cuts out the article and the photograph. “This is a real accomplishment,” he says while he's cutting. “You should be real proud of yourself.” He asks me to put my autograph on the article so when I'm famous someday, he can show people my name and say he met me in his store.
I sign my name across the bottom of the article in big scrawling artist letters. But before the manager tapes the article to the front of the counter where everybody can see it, I add one more thing.
I add a drawing of myself standing next to Sharice and Rhondell and Mr. Collins, with an arrow pointing to my head. I write my name above the arrow: James Harris III.
Just so everybody knows I was there.
One final fact to remember about tetrahedrons:
Because of its repeating pattern, the tetrahedron structure can expand to infinity. So, in theory, you can keep adding more and more tetrahedrons forever. …
O
ur math teacher Mr. Collins says that next year Washington Middle School is gonna build something even bigger, something even more amazing.
So if you are driving down Washington Boulevard someday, past the smoky good smells of Willy Q's Barbecue, past the Style R Us hair salon where they do nails like nobody's business, past the eye-popping red doors of the Sanctuary Baptist Church, and you get to a dead end—LOOK UP!
You just might see a forty-foot-tall silver and gold tetrahedron on the roof of our school building spinning to rap music.
Mr. Collins says nothing is impossible.
You want to fold silver or gold?
In 2002, a group of students at Alexander Hamilton School, an urban middle school in Cleveland, Ohio, completed what is called a “Stage 7” Sierpinski tetrahedron. They were one of two schools in Cleveland to attempt to build a structure of this record-breaking size and complexity.
The Alexander Hamilton team named their tetrahedron “The Rainbow Connection” because of the eye-catching and intricate rainbow-color pattern they created. The students worked at home, through their summer vacation, and after school to assemble the 16,384 smaller tetrahedrons needed to build the larger structure.
During the original project, the team used an Ellison paper-cutting machine with a custom-made die to cut out the small tetrahedron shapes. Although this saved one step in the laborious process, each one of the 16,384 pieces still had to be individually folded, glued, and joined together by hand, just as the characters describe. Hot-glue guns, which are often used for model-building and craft projects, proved to be the best tool for gluing the pieces and sections together, and the team assembled the large tetrahedron in stages.
During the writing of
All of the Above,
I read everything I could find about tetrahedrons—and also polished up some of my long-dormant math skills. I was often amazed by the connections between math and life. Mr. Collins' facts about tetrahedrons are based on the actual properties of the structure—and yes, the tetrahedron really can be expanded to infinity. But I'm not planning to try that anytime soon!
One mathematical note from Mr. Collins: Although some of the characters in the story use the terms “pyramid” and “tetrahedron” interchangeably, keep in mind that a tetrahedron is a special type of pyramid with a triangular base. Other types of pyramids with bases of different shapes would not be tetrahedrons.
Professor Waclaw Sierpinski, who is mentioned in the novel, is the person who first studied the properties of the tetrahedron as a flat, plane figure called a “gasket.” As Rhondell learns, he was a renowned math professor in Warsaw, Poland, during the early part of the twentieth century. Even though his house and personal library were destroyed by the Nazis during the Warsaw uprising of 1944, he went on to publish more than 700 research papers and fifty books in his lifetime.
The other characters, places, and events in this novel are fictional; however, I tried to capture the spirit and determination of the students who were part of the record-breaking 2002 team, and give readers a glimpse into the urban community where they live. The California school that built the “Stage 6” tetrahedron is not based on a particular school; however, several schools in the United States have built Stage 6 tetrahedrons of various heights.
I first saw the stunning rainbow tetrahedron during a visit to Alexander Hamilton School in late 2002. The magical sight caught my imagination. Later, I had the chance to talk to some of the past and present team members. At that time, the students were already hard at work on a new construction—an inverted Stage 6 tetrahedron, designed to spin on one of its points and match the colors of the Ohio flag for the state's bicentennial year.
However, Alexander Hamilton Middle School closed its old and well-worn doors three years later, and the school's tetrahedron projects ended. Its former students are now enrolled in other schools throughout Cleveland. The Alexander Hamilton team did submit their record to Guinness World Records for consideration. Although they did not receive a reply, the team and their teachers still believe that their 2002 tetrahedron set a math record. But as one student told me—it was just fun to be part of something.
—
Shelley Pearsall
I would like to gratefully acknowledge my editor, Jennifer Hunt, for bringing this story and its characters to life. A special thanks to Principal Hiawatha Shivers, and to the former tetrahedron team at Alexander Hamilton School and their always gracious teachers, James Wallace and Dianne Marsh, who answered my tetrahedron questions and shared their expertise with me. Thank you to math teachers Laura and Richard Little, as well as local students Cameron Granger and Artia Gunn, for reading early drafts of
All of the Above.
And finally, I can't forget to mention Bill and Sandi Pearsall, and my husband, Mike. Without their culinary advice and assistance in preparing (and tasting!) the recipes for this book, Willy Q and I would both be singing the blues.
A tetrahedron is a type of pyramid, made up of four triangles of equal size. Make a copy of this tetrahedron model. Color it, cut it out, and glue or tape it together to make your own tetrahedron.
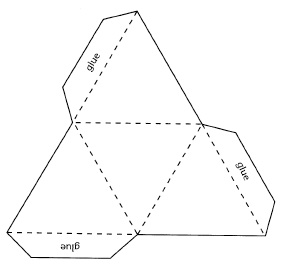
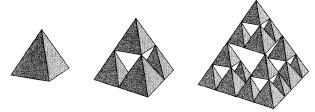
Next, tape your tetrahedrons together in sets of four to form larger tetrahedrons. These can be combined to form even larger tetrahedrons, if desired.
1.
James Harris III dislikes school and anything connected with it. How does James's home life affect his attitude toward school? How does Mr. Collins's approach to James pull him into the project? How does James's attitude toward himself change as he becomes involved in the project? How do others' opinions of James change?
2.
Although Mr. Collins has the idea for the tetrahedron project, he doesn't really expect that any of his students will want to participate (page 18). What is the motivation for each of the students to become involved in the project? How does Mr. Collins's lack of expertise in running a club help unite the students to work toward a common goal?
3.
James and Sharice both feel responsible for the destruction of the project. How does that guilt affect them? What actions do they take as a result of their feelings of responsibility? How do their guilt and shame affect the group and the completion of the project?
4.
What contributions, both positive and negative, do the adults make in the lives of James, Rhondell, Marcel, and Sharice? How do the actions of the adults affect the lives of the teens?
5.
Rhondell and her aunt Asia are the ones who find Sharice after her emotional breakdown. How does this one event alter the course of many lives?
6.
The author reveals that the role of each of the four students in the group mirror a tetrahedron in some way. Discuss the role each character plays in the group. How do each character's personality traits determine how he or she is like a tetrahedron? Reread Mr. Collins's words about tetrahedrons on pages 3, 99, 199, and 237 to gain some insight.
7.
In the end, how does the project change Rhondell, Marcel, James, Sharice, and Mr. Collins? Predict what the future may hold for these characters.
What's the Meaning of Life?
Find out inside this book…

