Antifragile: Things That Gain from Disorder (85 page)
Read Antifragile: Things That Gain from Disorder Online
Authors: Nassim Nicholas Taleb

Portfolio fallacies:
Note one fallacy promoted by Markowitz users:
portfolio theory entices people to diversify, hence it is better than nothing
. Wrong, you finance fools: it pushes them to optimize, hence overallocate. It does not drive people to take less risk based on diversification, but causes them to take more open positions owing to perception of offsetting statistical properties—making them vulnerable to model error, and especially vulnerable to the underestimation of tail events. To see how, consider two investors facing a choice of allocation across three items: cash, and securities
A
and
B
. The investor who does not know the statistical properties of
A
and
B
and knows he doesn’t know will allocate, say, the portion he does not want to lose to cash, the rest into
A
and
B
—according to whatever heuristic has been in traditional use. The investor who thinks he knows the statistical properties, with parameters σ
A
, σ
B
, ρ
A
,
B
, will allocate
ω
A
,
ω
B
in a way to put the total risk at some target level (let us ignore the expected return for this). The lower his perception of the correlation ρ
A
,
B
, the worse his exposure to model error. Assuming he thinks that the correlation ρ
A
,
B
, is 0, he will be overallocated by
1
⁄
3
for extreme events. But if the poor investor has the illusion that the correlation is −1, he will be maximally overallocated to his
A
and
B
investments. If the investor uses leverage, we end up with the story of Long-Term Capital Management, which turned out to be fooled by the parameters. (In real life, unlike in economic papers, things tend to change; for Baal’s sake, they change!) We can repeat the idea for each parameter σ and see how lower perception of this σ leads to overallocation.
I noticed as a trader—and obsessed over the idea—that correlations were never the same in different measurements. Unstable would be a mild word for them: 0.8 over a long period becomes −0.2 over another long period. A pure sucker game. At times of stress, correlations experience even more abrupt changes—without any reliable regularity, in spite of attempts to model “stress correlations.” Taleb (1997) deals with the effects of stochastic correlations: One is only safe shorting a correlation at 1, and buying it at −1—which seems to correspond to what the 1
/n
heuristic does.
Kelly Criterion vs. Markowitz:
In order to implement a full Markowitz-style optimization, one needs to know the entire joint probability distribution of all assets for the entire future, plus the exact utility function for wealth at all future times. And without errors! (We saw that estimation errors make the system explode.) Kelly’s method, developed around the same period, requires no joint distribution or utility function. In practice one needs the ratio of expected profit to worst-case return—dynamically adjusted to avoid ruin. In the case of barbell transformations, the worst case is guaranteed. And model error is much, much milder under Kelly criterion. Thorp (1971, 1998), Haigh (2000).
The formidable Aaron Brown holds that Kelly’s ideas were rejected by economists—in spite of the practical appeal—because of their love of general theories for all asset prices.
Note that bounded trial and error is compatible with the Kelly criterion when one has an idea of the potential return—even when one is ignorant of the returns, if losses are bounded, the payoff will be robust and the method should outperform that of Fragilista Markowitz.
Corporate Finance:
In short, corporate finance seems to be based on point projections, not distributional projections; thus if one perturbates cash flow projections, say, in the Gordon valuation model, replacing the fixed—and known—growth (and other parameters) by continuously varying jumps (particularly under fat-tailed distributions), companies deemed “expensive,” or those with high growth, but low earnings, could markedly increase in expected value, something the market prices heuristically but without explicit reason.
Conclusion and summary:
Something the economics establishment has been missing is that having the right model (which is a very generous assumption), but being uncertain about the parameters will invariably lead to an increase in fragility in the presence of convexity and nonlinearities.
Now the meat, beyond economics, the more general problem with probability and its mismeasurement.
Nonlinear Responses to Model Parameters
Rare events have a certain property—missed so far at the time of this writing. We deal with them using a model, a mathematical contraption that takes input parameters and outputs the probability. The more parameter uncertainty there is in a model designed to compute probabilities, the more small probabilities tend to be underestimated. Simply, small probabilities are convex to errors of computation, as an airplane ride is concave to errors and disturbances (remember, it gets longer, not shorter). The more sources of disturbance one forgets to take into account, the longer the airplane ride compared to the naive estimation.
We all know that to compute probability using a standard Normal statistical distribution, one needs a parameter called
standard deviation
—or something similar that characterizes the scale or dispersion of outcomes. But uncertainty about such standard deviation has the effect of making the small probabilities rise. For instance, for a deviation that is called “three sigma,” events that should take place no more than one in 740 observations, the probability rises by 60% if one moves the standard deviation up by 5%, and drops by 40% if we move the standard deviation down by 5%. So if your error is on average a tiny 5%, the underestimation from a naive model is about 20%. Great asymmetry, but nothing yet. It gets worse as one looks for more deviations, the “six sigma” ones (alas, chronically frequent in economics): a rise of five times more. The rarer the event (i.e., the higher the “sigma”), the worse the effect from small uncertainty about what to put in the equation. With events such as ten sigma, the difference is more than a billion times. We can use the argument to show how smaller and smaller probabilities require more precision in computation. The smaller the probability, the more a small, very small rounding in the computation makes the asymmetry massively insignificant. For tiny, very small probabilities, you need near-infinite precision in the parameters; the slightest uncertainty there causes mayhem. They are very convex to perturbations. This in a way is the argument I’ve used to show that small probabilities are incomputable, even if one has the right model—which we of course don’t.
The same argument relates to deriving probabilities nonparametrically, from past frequencies. If the probability gets close to 1/ sample size, the error explodes.
This of course explains the error of Fukushima. Similar to Fannie Mae. To summarize, small probabilities increase in an accelerated manner as one changes the parameter that enters their computation.
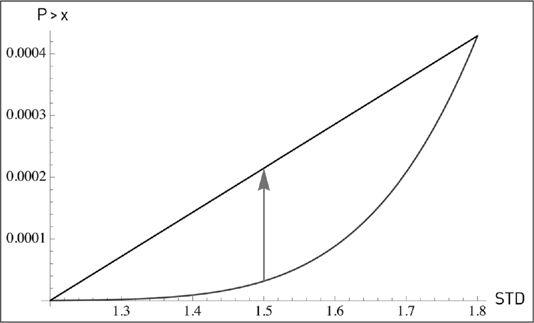
FIGURE 38.
The probability is convex to standard deviation in a Gaussian model. The plot shows the STD effect on P>x, and compares P>6 with an STD of 1.5 compared to P>6 assuming a linear combination of 1.2 and 1.8 (here a(1)=1/5).
The worrisome fact is that a perturbation in σ extends well into the tail of the distribution in a convex way; the risks of a portfolio that is sensitive to the tails
would explode. That is, we are still here in the Gaussian world! Such explosive uncertainty isn’t the result of natural fat tails in the distribution, merely small imprecision about a future parameter. It is just epistemic! So those who use these models while admitting parameters uncertainty are necessarily committing a severe inconsistency.
2
Of course, uncertainty explodes even more when we replicate conditions of the non-Gaussian real world upon perturbating tail exponents. Even with a powerlaw distribution, the results are severe, particularly under variations of the tail exponent as these have massive consequences. Really, fat tails mean incomputability of tail events, little else.
Using the earlier statement that
estimation implies error,
let us extend the logic: errors have errors; these in turn have errors. Taking into account the effect makes all small probabilities rise regardless of model—even in the Gaussian—to the point of reaching fat tails and powerlaw effects (even the so-called infinite variance) when higher orders of uncertainty are large. Even taking a Gaussian with σ the standard deviation having a proportional error
a
(1);
a
(1) has an error rate
a
(2), etc. Now it depends on the higher order error rate
a
(
n
) related to
a
(
n
−1); if these are in constant proportion, then we converge to a very thick-tailed distribution. If proportional errors decline, we still have fat tails. In all cases mere error is not a good thing for small probability.
The sad part is that getting people to accept that every measure has an error has been nearly impossible—the event in Fukushima held to happen once per million years would turn into one per 30 if one percolates the different layers of uncertainty in the adequate manner.
1
The difference between the two sides of Jensen’s inequality corresponds to a notion in information theory, the Bregman divergence. Briys, Magdalou, and Nock, 2012.
2
This further shows the defects of the notion of “Knightian uncertainty,” since
all tails
are uncertain under the slightest perturbation and their effect is severe in fat-tailed domains, that is, economic life.
These are both additional readings and ideas that came to me after the composition of the book, like whether God is considered robust or antifragile by theologians or the history of measurement as a sucker problem in the probability domain. As to further reading, I am avoiding the duplication of those mentioned in earlier books, particularly those concerning the philosophical problem of induction, Black Swan problems, and the psychology of uncertainty. I managed to bury some mathematical material in the text without Alexis K., the math-phobic London editor, catching me (particularly my definition of fragility in the notes for
Book V
and my summary derivation of “small is beautiful”). Note that there are more involved technical discussions on the Web.
Seclusion:
Since
The Black Swan,
I’ve spent 1,150 days in physical seclusion, a soothing state of more than three hundred days a year with minimal contact with the outside world—plus twenty years of thinking about the problem of nonlinearities and nonlinear exposures. So I’ve sort of lost patience with institutional and cosmetic knowledge. Science and knowledge are convincing and deepened rigorous argument taken to its conclusion, not naive (
via positiva
) empiricism or fluff, which is why I refuse the commoditized (and highly gamed) journalistic idea of “reference”—rather, “further reading.” My results should not depend, and do not depend on a single paper or result, except for
via negativa
debunking—these are illustrative.Charlatans:
In the “fourth quadrant” paper published in
International Journal of Forecasting
(one of the backup documents for
The Black Swan
that had been sitting on the Web) I showed
empirically
using all economic data available that fat tails are both severe and intractable—hence all methods with “squares” don’t work with socioeconomic variables: regression, standard deviation, correlation, etc. (technically 80% of the Kurtosis in 10,000 pieces of data can come from
one single
observation, meaning all measures of fat tails are just sampling errors). This is a very strong
via negativa
statement: it means we can’t use covariance matrices—they are unreliable and uninformative. Actually just accepting fat tails would have led us to such result—no need for empiricism; I processed the data nevertheless. Now any honest scientific profession would say: “what do we do
with such evidence?”—the economics and finance establishment just ignored it. A bunch of charlatans, by any scientific norm and ethical metric. Many “Nobels” (Engle, Merton, Scholes, Markowitz, Miller, Samuelson, Sharpe, and a few more) have their results grounded in such central assumptions, and all their works would evaporate otherwise. Charlatans (and fragilistas) do well in institutions. It is a matter of ethics; see notes on
Book VII
.For our purpose here, I ignore any economic paper that uses regression in fat-tailed domains—as just hot air—except in some cases, such as Pritchet (2001), where the result is not impacted by fat tails.