Birth of a Theorem: A Mathematical Adventure (42 page)

Cédric Villani

EPILOGUE

Budapest

February 24, 2011

Four bottles lined up in a row on a small rickety table. My mind most pleasantly clouded by a fine red wine from the famous Villány region, I strain to follow Gábor’s detailed analysis of the comparative virtues of these four white wines. Young, dry, sweet … I am incapable of choosing among them.

After two helpings of goulash and apple pie, the children run off to take pictures of everything in the small apartment, dominated by a giant screen in the main room. Claire helps me select a sweet, organic Tokay. Gábor’s wife, Réka, serves a superb cappuccino made with deliciously creamy milk.

Gábor speaks of his native land, and of his childhood, when kids happily spent twelve hours a week doing mathematics and the Olympiad problems were announced on television every year—problems that Réka still remembers.

He speaks of his extraordinary language, a distant cousin of Finnish, from which it branched off a thousand years ago. A language that forces the listener to be constantly alert, constantly wondering whether the next word is going to utterly transform the meaning he has registered so far. Is this why Hungary produced more legendary mathematicians and physicists than any other country during the first half of the twentieth century? The land of Erd
ő
s, von Neumann, Fejér, Riesz, Teller, Wigner, Szilárd, Lax, Pólya, and all the others.

“The Jews played a vital role!” Gábor insists. “For a time our country was the least anti-Semitic in this part of the world. Jewish thinkers flocked to Hungary and dramatically increased its intellectual wealth. Then the winds shifted: they were no longer welcome, and, alas, they went away.…”

*   *   *

Gábor discovered the Gömböc, an incredible shape that Vladimir Arnold felt sure must exist: solid, homogeneous, having only one stable point of equilibrium and one unstable point. A minimal superstable shape, in other words, which always comes back to its equilibrium position no matter how you set it down on a flat surface. Like a Weeble—except the Weeble is weighted at the bottom, whereas in a Gömböc the weight is evenly distributed.

The moment I arrived in Budapest, I heard people talking about this object that Gábor Domokos had discovered. I pictured a Gömböc on display in the library of the IHP in Paris. But first of all I wanted to see it, to convince myself that such a thing really exists! A quick exchange of emails was all it took. My institute would be very honored to exhibit your marvelous object. I would be very honored if my discovery were to be recognized by your prestigious institute, I’ll be at your talk tomorrow, would you be able to come to my house for lunch the day after? Sounds great, I’m eager to meet you.

“What a beautiful talk you gave yesterday at the university!” Gábor exclaimed. “What a talk! It was so beautiful, one would have sworn that Boltzmann himself was in the room. In our midst! I’m not kidding, what a beautiful talk!”

He described the scene for Claire: “The room was overheated and too small for the audience, the projector didn’t arrive, your husband had to be careful he didn’t trip over all the wires that were lying around, the blackboard wouldn’t stay in place, it kept slipping—but it didn’t bother him in the least! He talked for an hour and a half! What a pleasure!”

We raised our glasses to Boltzmann, to the brotherhood among mathematicians of all countries—and to my article on Landau damping, which, after a bit more toing and froing with the referees, was officially accepted yesterday for publication by
Acta Mathematica.

The sweet Tokay was going down easily, Gábor went on talking. About his experience at the International Congress on Industrial and Applied Mathematics in Hamburg fifteen years ago, in 1995. A luncheon had been organized with Arnold: everyone except the guest of honor had to pay. Gábor signed up at once—even though it would cost him half of his miserably small travel budget. Came the day, he was so intimidated he didn’t dare even to speak to the great man!

But the next day, quite by chance, Gábor crossed paths with his hero again. Arnold was unsuccessfully trying to fend off a pest (I solved your problem ten years ago, I really don’t have time to listen to your proof) and immediately took advantage of Gábor’s unexpected appearance in order to extricate himself (No, really, I’m sorry, I have an appointment with this gentleman here).

As it turned out, Arnold was curious to know more about the strangely silent guest from the day before. “I saw you at the luncheon yesterday. I know you’re from Hungary and that the meal was very expensive for you, so if you’ve got something to say to me, now’s a good time!”

Gábor described his research and Arnold told him he was going about it the wrong way. In the course of their conversation, Arnold confided his belief in the existence of a minimum stable shape: a shape having two equilibria, only one of which is stable.

These few minutes changed Gábor’s life. Little did he imagine that he would spend fully twelve years seeking the famously elusive shape. Together with Réka, he collected and experimented with thousands of pebbles before concluding that it didn’t exist in nature and would have to be created. Perhaps by deforming a sphere to produce a spheroid—since true spheroids are seldom found in nature.

Finally, in 2006, Gábor found the shape he was looking for with the help of his student Péter Vàrkony, whom chance had made his partner. He named it Gömböc, the Hungarian word for “spheroid.”

The first Gömböc was abstract, so close to a sphere that the difference was imperceptible to the naked eye. But gradually its creators succeeded in deforming it more and more, to the point that it looked like a cross between a tennis ball and a prehistoric stone carving, while yet retaining the crucial property of having only one stable and one unstable equilibrium position!

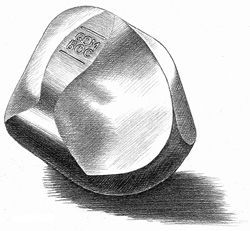
Gábor hands me an enormous Gömböc made out of Plexiglas.

“Isn’t it beautiful? Twelve years of research! When the Chinese see it they think it’s a three-dimensional representation of yin and yang! I gave the very first one to Arnold for his seventieth birthday. I’ll send you a fine specimen, cast in metal—and numbered 1928, the date your institute was founded.”

Another glass of Tokay. The children are taking pictures of the images streaming across the giant screen. Réka is taking pictures of the children taking pictures. Gábor goes on talking. I go on listening, fascinated by his story. An eternal story, a mathematical story, of quests, of dreams—and of passion.

A Note on the Translation

The English translation of
Théorème Vivant
differs in many small ways from the second French edition, incorporating additional corrections and clarifying certain passages. Still, the temptation to be as precise as possible has been resisted. The book is meant chiefly as a work of literary imagination. Whatever else it may be, it is in no way, shape, or form a scientific treatise.

At the author’s suggestion, a brief section of notes has been included as a courtesy to readers who may be unacquainted with some of the references in the text, particularly to aspects of popular culture. No attempt has been made to expand upon, much less to explain, fine points of mathematical detail, many of which will be unfamiliar even to professional mathematicians. The technical material, though not actually irrelevant, is in any case inessential to the story
C
é
dric Villani
tells in this book.

Notes

The page numbers for the notes that appear in the print version of this title are not in your e-book. Please use the search function on your e-reading device to search for the relevant passages documented or discussed.

THREE

the fiendishly gifted surgeon
: Black Jack is a character created by the Japanese artist and animator Tezuka Osamu (1928–89), the legendary “father of manga.”

would have resumed his superhuman labors
: In January 1962 Landau was nearly killed in a car accident, which left him in a coma for two months. He never completely recovered from his injuries, and died six years later.

FIVE

the ones that David B. records:
The pen name of the French artist and writer Pierre-François (“David”) Beauchard.

Vincent Beffara isn’t here
:
In real life, Beffara is a mathematician at ENS-Lyon.

SIX

Gott im Himmel!
:
Echoing Kurt Weill’s “Ballad of Marie Saunders.”

Cédurak go!
:
A personal slogan from the author’s school days at Lycée Louis-Le-Grand in Paris, adapted from the command (“Goldorak go!”) issued by the space-fighter hero of a popular Japanese anime of the same name from the late 1970s.

(chapter 3, exercise A.1.a):
Villani gives a corrected version of the exercise that appears in the original 1991 edition of Alinhac and Gérard’s book, the one he actually consulted. A revised English edition was published by the American Mathematics Society in 2007, but the alterations made by the authors to the statement of this exercise were apparently marred by typos—hence the very minor revisions silently made here.

EIGHT

Even the name of the formula’s author I had forgotten:
The formula is named after the Italian priest Francesco Faà di Bruno (1825–88), beatified by the Church on the centennial of his death. Faà di Bruno studied mathematics under Cauchy and Le Verrier in Paris.

(Arbogast 1800, Faà di Bruno 1855)
:
The formula appears to have been first stated by the French mathematician Louis François Antoine Arbogast (1759–1803).

NINE

the project with Alessio and Ludovic:
Alessio Figalli, then at the École Polytechnique in Palaiseau (now at the University of Texas–Austin), and Ludovic Rifford, at the Université de Nice–Sophia Antipolis.

On stories I really like
:
A line from William Sheller’s 1979 single “Oh! J’cours tout seul.”

The general criterion we’ve proposed for curvature-dimension:
Lott–Sturm–Villani spaces, as they are now called—after work done by the author in collaboration with John Lott, at Berkeley, and independently by Karl-Theodor Sturm, at the University of Bonn.

TEN

Claire’s turn to get hooked on it:
The manga
Death Note
,
written by Tsugumi Ohba and illustrated by Takeshi Obata, was serialized between 2003 and 2006, when the first anime episodes, directed by Tetsuro Araki, were aired on Japanese television. A DVD edition followed shortly thereafter.

ELEVEN

Fischer and Erd
ő
s were Hungarian:
Erd
ő
s was fully Hungarian by birth, Fischer partially (his biological father seems almost certainly to have been a Hungarian Jewish physicist named Paul Nemeny).

Alexander Grothendieck, a living legend:
Grothendieck passed away, not long before this book went to press, on November 13, 2014.

From the liner notes to
Final Report
(1999):
Excerpted from the brief history of Do Not Erase written by the historian Marshall Poe (vocals, rhythm guitar) that appears on the cover of its only recording. The other members of DNE were mathematicians: Carol Namkoong (drums, backing vocals), David Renard (lead guitar), Konstanze Rietsch (vocals), Peter Trapa (bass), and Lindi Wahl (vocals). The full text of the liner notes is available at
www.math.utah.edu/~ptrapa/finalreport/linernotes.html
.