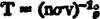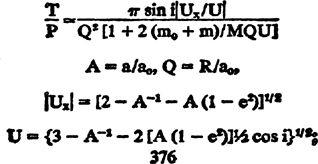Broca's Brain (52 page)
Authors: Carl Sagan

CHAPTER 7
APPENDIX
1
Simple Collision Physics Discussion of the Probability of a Recent Collision with the Earth by a Massive Member of the Solar System
WE HERE CONSIDER
the probability that a massive object of the sort considered by Velikovsky to be ejected from Jupiter might impact Earth. Velikovsky proposes that a grazing or near-collision occurred between this comet and the Earth. We will subsume this idea under the designation “collision” below. Consider a spherical object of radius R moving among other objects of similar size. Collision will occur when the centers of the objects are 2R distant. We may then speak of an effective collision cross section of σ = π(2R)
2
= 4πR
2
; this is the target area which the center of the moving object must strike in order for a collision to occur. Let us assume that only one such object (Velikovsky’s comet) is moving and that the others (the planets in the inner solar system) are stationary. This neglect of the motion of the planets of the inner solar system can be shown to introduce errors smaller than a factor of 2. Let the comet be moving at a velocity v and let the space density of potential targets (the planets of the inner solar system) be n. We will use units in which R is in centimeters (cm), σ is in cm
2
, v is in cm/sec, and n is in planets per cm
3
; n is obviously a very small number.
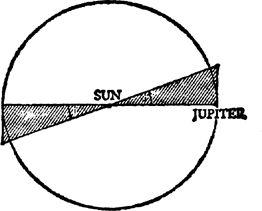
While comets have a wide range of orbital inclinations to the ecliptic plane, we will be making the most generous assumptions for Velikovsky’s hypothesis if we assume the smallest plausible value for this inclination. If there were no
restriction on the orbital inclination of the comet, it would have equal likelihood of moving anywhere in a volume centered on the Sun and of radius r = 5 astronomical units (1 a.u. = 1.5 × 10
12
cm), the semi-major axis of the orbit of Jupiter. The larger the volume in which the comet can move, the less likely is any collision of it with another object. Because of Jupiter’s rapid rotation, any object flung out from its interior will have a tendency to move in the planet’s equatorial plane, which is inclined by 1.2° to the plane of the Earth’s revolution about the Sun. However, for the comet to reach the inner part of the solar system at all, the ejection event must be sufficiently energetic that virtually any value of its orbital inclination, i, is plausible. A generous lower limit is then i = 1.2°. We therefore consider the comet to move (see diagram) in an orbit contained somewhere in a wedge-shaped volume, centered on the Sun (the comet’s orbit must have the Sun at one focus), and of half-angle i. Its volume is then (4/3)πr
3
sin i = 4 × 10
40
cm
3
, only 2 percent the full volume of a sphere of radius
r.
Since in that volume there are (disregarding the asteroids) three or four planets, the space density of targets relevant for our problem is about 10
−40
planets/cm
8
. A typical relative velocity of a comet or other object moving on an eccentric orbit in the inner solar system might be about 20 km/sec. The radius of the Earth is R = 6.3 × 10
8
cm, which is almost exactly the radius of the planet Venus as well.
Now let us imagine that the elliptical path of the comet is, in our mind’s eye, straightened out, and that it travels for some time T until it impacts a planet. During that time it will have carved out an imaginary tunnel behind it of volume σvT cm
3
, and in that volume there must be just one planet.
Wedge-shaped volume occupied by Velikovsky’s comet.
But 1/n is also the volume containing one planet. Therefore, the two quantities are equal and
T is called the mean free time.
In reality, of course, the comet will be traveling on an elliptical orbit, and the time for collision will be influenced to some degree by gravitational forces. However, it is easy to show (see, for example, Urey, 1951) that for typical values of v and relatively brief excursions of solar system history such as Velikovsky is considering, the gravitational effects are to increase the effective collision cross section σ by a small quantity, and a rough calculation using the above equation must give approximately the right results.
The objects which have, since the earliest history of the solar system, produced impact craters on the Moon, Earth and the inner planets are ones in highly eccentric orbits: the comets and, especially, the Apollo object—which are either dead comets or asteroids. Using simple equations for the mean free time, astronomers are able to account to good accuracy for, say, the number of craters on the Moon, Mercury or Mars produced since the formation of these objects: they are the results of the occasional collision of an Apollo object or, more rarely, a comet with the lunar or planetary surface. Likewise, the equation predicts correctly the age of the most recent impact craters on Earth such as Meteor Crater, Arizona. These quantitative agreements between observations and simple collision physics provide some substantial assurance that the same considerations properly apply to the present problem.
We are now able to make some calculations with regard to Velikovsky’s fundamental hypothesis. At the present time there are no Apollo objects with diameters larger than a few tens of kilometers. The sizes of objects in the asteroid belt, and indeed anywhere else where collisions determine sizes, are understood by comminution physics. The number of objects in a given size range is proportional to the radius of the object to some negative power, usually in the range of 2 to 4. If, therefore, Velikovsky’s proto-Venus comet were a member of some family of objects like the Apollo objects or the comets, the chance of finding one Velikovskian comet 6,000 km in radius would be far less than one-millionth of the chance of finding one some 10 km in radius.
A more probable number is a billion times less likely, but let us give the benefit of the doubt to Velikovsky.
Since there are about ten Apollo objects larger than about 10 km in radius, the chance of there being one Velikovskian comet is then much less than 100,000-to-1 odds against the proposition. The steady-state abundance of such an object would then be (for r = 4 a.u., and i = 1.2
0
) n = (10 × 10
−5
)/4 × 10
40
= 2.5 × 10
−45
Velikovskian comets/cm
3
. The mean free time for collision with Earth would then be T = 1/(nσv) = 1/[(2.5 × 10
−45
cm
−3
) × (5 × 10
18
cm
2
) × (2 × 10
6
cm sec
−1
)] = 4 × 10
21
secs 10
10
14
years which is much greater than the age of the solar system (5 × 10
9
years). That is, if the Velikovskian comet were part of the population of other colliding debris in the inner solar system, it would be such a rare object that it would essentially never collide with Earth.
But instead, let us grant Velikovsky’s hypothesis for the sake of argument and ask how long his comet would require, after ejection from Jupiter, to collide with a planet in the inner solar system. Then,
n
applies to the abundance of planetary targets rather than Velikovskian comets, and T = 1/[(10
−40
cm
−3
) × (5 × 10
18
cm
2
) × (2 × 10
6
cm sec
−1
)] = 10
18
secs 3 × 10
3 × 10
7
years. Thus, the chance of Velikovsky’s “comet” making a single full or grazing collision with Earth within the last few thousand years is (3 × 10
4
)/(3 × 10
7
) = 10
−3
, or one chance in 1,000—if it is independent of the other debris populations. If it is part of such populations, the odds rise to (3 × 10
4
)/10
14
= 3 × 10
−10
, or one chance in 3 billion.
A more exact formulation of orbital-collision theory can be found in the classic paper by Ernst Öpik (1951). He considers a target body of mass
m
0
with orbital elements a
0
, e
0
= i
0
= 0 in orbit about a central body of mass M. Then, a test body of mass m with orbital elements a, e, i and period P has a characteristic time T before approaching within distance R of the target body, where