Collected Essays (40 page)
Authors: Rudy Rucker


Rudy Rockets, a detail of the Rudy Set.
Iterated Functions and the Old Quadratic Julia and Mandelbrot Sets
A map in the plane is some system for finding an image P’ of each point P. If f is a map in the plane, and f maps z into z’, I can express this either by writing z’ = f(z) or by writing z—f—> z’. Given an f and a z, we can define a sequence zn by:
z0 = z, z1 = f(z), z2 = f(z1, and in general, zn+1 = f(zn).
In terms of f,
z—f—> z1—f—> z2—f—> z3—f—> z4—f—>…
For some starting values of z, the zn sequence hops around within some bounded region of the plane, and we say z is bounded under f. And for other start values of z, the zn sequence heads off across the plane towards infinity.
The
Julia set
for a map f is defined as the set of all z in the plane which are bounded under f. Symbolically, the Julia set for f is { z : z—f—> FINITE )}.
The quadratic map fc given by fc(z) = z^2 + c has been widely studied. The Julia set for the fc map is called Jc. They became popular in the 1980s, along with a kind of “directory set” called the Mandelbrot set, which can be defined equivalently as M = { c : Jc is connected}, or , M = { c : the origin is in Jc }.
The Cubic Julia Sets
Okay, now for the good stuff!!! The maps which the Cubic Julias and Cubic Mandelbrots are based on have the form fkc, with fkc(z) = z^3 - 3*k*z + c
For each fkc we can define a cubic Julia set Jkc by: Jkc = { z: z—fkc—>FINITE }.
Why do I write fkc(z) in the particular form that I do? As discussed in Bodil Branner and John Hubbard, “The Iteration of Cubic Polynomials, Part I: The Global Topology of Parameter Space,” if you write polynomials in certain special ways, it’s easier to locate the so-called critical points of the polynomials. More on this point later on. For now, the point is simply that, by moving the origin of our coordinate system and a judicious choice of k and c, we can in fact write any cubic polynomial in the indicated form.
To graphically represent the Jkc sets, each pixel position on the screen is identified with a distinct complex number c, and we look at c’s behavior under the map, which generates successive zn values. If zn is more than, say, 4 units way from the origin, we assume the sequence is headed for infinity, and give the pixel a color based on the value of n. And if zn stays within the boundary distance for as many steps as we check, then we assume that the pixel represents a point inside the set, and we typically color these points black.
Unlike in the quadratic case, these cubic Julia sets Jkc are generally not symmetric. Some of them are connected, like this one.

Julia Cubic Asteroids
Some of the Jkc, which we won’t show, are made of numerous separate connected patches, and some are totally disconnected, like clouds of dust.
It has been proved that Jkc is in fact connected if and only if both the complex numbers k and -k are in Jkc. These are the critical points of the fkc map that I was talking about above. We’ve written the cubic in the special form z^3 - 3*k*z + c precisely so that the critical points have this simple definition: k and -k.
As Jkc is not symmetric, it may happen that only one of k or -k is in Jkc. Jkc is connected only when
both
of these critical points are in Jkc.
Cubic Mandelbrot Sets
The four-dimensional set of all complex pairs k and c such that Jkc is connected is known as the Cubic Connectedness map, or the CCM. Why do I say four dimensional? Well, k has two numbers inside it in the form a+bi, and c also holds two numbers. Ranging over four parameters gives you a 4D space.
The CCM set has been studied by Adrian Douady, John Hubbard and John Milnor—as well as the paper mentioned above, see Adrian Douady and John Hubbard, “On the Dynamics of Polynomial-like Mappings,” and Bodil Branner and John Hubbard, “The Iteration of Cubic Polynomials Part II: Patterns and Parapatterns” (Love the title.)
I never have understood why the Cubic Connectedness Map isn’t much better known! For some odd reason, my fellow fractal fanatics have consistently snubbed or misunderstood this incredibly rich vein of gnarl.
CCM = { (k, c) : Jkc is connected}
or, putting it differently,
CCM = { (k, c) : ( k—fkc—> FINITE ) AND ( -k—fkc—> FINITE ) }
One way to depict the CCM is to show various two-dimensional cross-sections of it. These cross-sections are what we call Cubic Mandelbrot sets. If, for instance, k is fixed, then we can look at the Cubic Mandelbrot set Mk.
Mk = { c : Jkc is connected}, or
Mk = { c : ( k—fkc—>FINITE ) AND ( -k—fkc—>FINITE ) }.
It turns out that that Mk is symmetric around the origin, that is, if c is in Mk, so is -c. If k = 0+0i, one gets a degenerate Mk with fourfold symmetry; this is the default Cubic Mandelbrot set. This rather boring fractal is, sadly, the only well-known cubic Mandelbrot. Most fractal explorers neglect all the other—much more interesting—Mk.

The boring default cubic Mandelbrot
Note that a small change in the K parameter makes it more interesting.
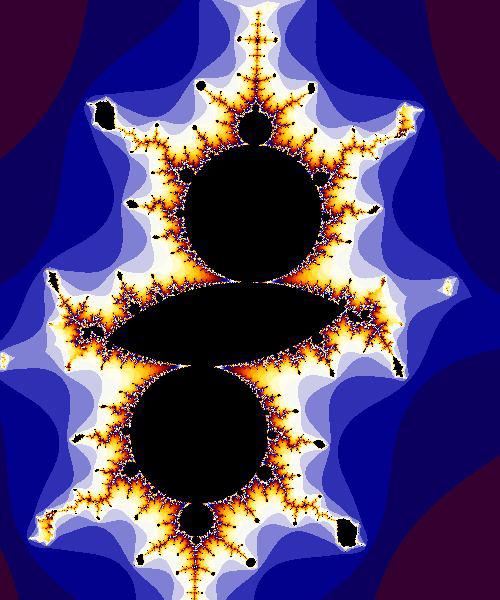
The interesting Mandel Cubic Stack
And things get better.

Detail of Mandel Cubic Invasion Of The Hrull
One often sees small replicas of the pieces of the quadratic Mandelbrot set inside the Mk, though sometimes with wedges cut out of them.

Detail of Mandel Cubic Pac Man
As I mentioned above, the full CCM is in fact four-dimensional, and this shows up in the fact that many of the bud cross-sections have pieces missing from them. As an aid to mathematical visualization, I think of it this way. The CCM is like a three dimensional solid which is free to move pieces of itself to arbitrary time locations. Thus if a section of a bud seems to have the right half missing, we might think of the left half of the bud as being in Monday and the right half of the bud as being in Tuesday, with your cross-section being computed at the Monday time coordinate. I use time not at all in a physical sense here, but simply for the vividness of the image.
Some of the Mk details are fairly amazing.

Detail of the WhoopDiDoo Cubic Mandelbrot Set.
And here’s another.

