Data Mining (14 page)
Authors: Mehmed Kantardzic

(a)
find the outliers using the distance-based technique if
(i)
the threshold distance is 4, and threshold fraction p for non-neighbor samples is 3, and
(ii)
the threshold distance is 6, and threshold fraction p for non-neighbor samples is 2.
(b)
Describe the procedure and interpret the results of outlier detection based on mean values and variances for each dimension separately.
12. Discuss the applications in which you would prefer to use EMA instead of MA.
13. If your data set contains missing values, discuss the basic analyses and corresponding decisions you will take in the preprocessing phase of the data-mining process.
14. Develop a software tool for the detection of outliers if the data for preprocessing are given in the form of a flat file with n-dimensional samples.
15. The set of seven 2-D samples is given in the following table. Check if we have outliers in the data set. Explain and discuss your answer.
| Sample # | X | Y |
| 1 | 1 | 3 |
| 2 | 7 | 1 |
| 3 | 2 | 4 |
| 4 | 6 | 3 |
| 5 | 4 | 2 |
| 6 | 2 | 2 |
| 7 | 7 | 2 |
16. Given the data set of 10 3-D samples: {(1,2,0), (3,1,4), (2,1,5), (0,1,6), (2,4,3), (4,4,2), (5,2,1), (7,7,7), (0,0,0), (3,3,3)}, is the sample S4 = (0,1,6) outlier if the threshold values for the distance d = 6, and for the number of samples in the neighborhood p > 2? (Note: Use distance-based outlier-detection technique.)
17. What is the difference between
nominal
and
ordinal
data? Give examples.
18. Using the method of
distance-based outliers detection
find the outliers in the set
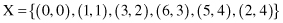
if the criterion is that at least the fraction p ≥ 3 of the samples in X lies at a distance d greater than 4.
19. What will be normalized values (using
min-max normalization
of data for the range [−1, 1]) for the data set X?

20. Every attribute in 6-D samples is described with one out of three numerical values: {0, 0.5, 1}. If there exist samples for all possible combinations of attribute values
(a)
What will be the number of samples in a data set, and
(b)
What will be the expected distance between points in a 6-D space?
21. Classify the following attributes as
binary, discrete, or continuous
. Also, classify them as
qualitative
(
nominal or ordinal
) or
quantitative
(
interval or ratio
). Some cases may have more than one interpretation, so briefly indicate your reasoning (e.g., age in years; answer: discrete, quantitative, ratio).
(a)
Time in terms of AM or PM.
(b)
Brightness as measured by a light meter.
(c)
Brightness as measured by people’s judgment.
(d)
Angles as measured in degrees between 0 and 360.
(e)
Bronze, Silver, and Gold medals at the Olympics.
(f)
Height above sea level.
(g)
Number of patients in a hospital.
(h)
ISBN numbers for books.
(i)
Ability to pass light in terms of the following values: opaque, translucent, transparent.
(j)
Military rank.
(k)
Distance from the center of campus.
(l)
Density of a substance in grams per cubic centimeter.
(m)
Coats check number when you attend the event.
2.8 REFERENCES FOR FURTHER STUDY
Bischoff, J., T. Alexander,
Data Warehouse: Practical Advice from the Experts
, Prentice Hall, Upper Saddle River, NJ, 1997.
The objective of a data warehouse is to provide any data, anywhere, anytime in a timely manner at a reasonable cost. Different techniques used to preprocess the data in warehouses reduce the effort in initial phases of data mining.
Cios, K.J., W. Pedrycz, R. W. Swiniarski, L. A. Kurgan,
Data Mining: A Knowledge Discovery Approach
, Springer, New York, 2007.
This comprehensive textbook on data mining details the unique steps of the knowledge discovery process that prescribe the sequence in which data-mining projects should be performed.
Data Mining
offers an authoritative treatment of all development phases from problem and data understanding through data preprocessing to deployment of the results. This knowledge-discovery approach is what distinguishes this book from other texts in the area. It concentrates on data preparation, clustering and association-rule learning (required for processing unsupervised data), decision trees, rule induction algorithms, neural networks, and many other data-mining methods, focusing predominantly on those which have proven successful in data-mining projects.
Hand, D., H. Mannila, P. Smith,
Principles of Data Mining
, MIT Press, Cambridge, MA, 2001.
The book consists of three sections. The first, foundations, provides a tutorial overview of the principles underlying data-mining algorithms and their applications. The second section, data-mining algorithms, shows how algorithms are constructed to solve specific problems in a principled manner. The third section shows how all of the preceding analyses fit together when applied to real-world data-mining problems.
Hodge, J. V., J. Austin, A Survey of Outlier Detection Methodologies,
Artificial Intelligence Review
, Vol. 22, No. 2, October 2004, pp. 85–127.
The original outlier-detection methods were arbitrary but now, principled and systematic techniques are used, drawn from the full gamut of Computer Science and Statistics. In this paper, a survey of contemporary techniques for outlier detection is introduced. The authors identify respective motivations and distinguish advantages and disadvantages of these techniques in a comparative review.
Ben-Gal, I., Outlier Detection, in
Data Mining and Knowledge Discovery Handbook: A Complete Guide for Practitioners and Researchers
, O. Maimon and L. Rockach eds., Kluwer Academic Publishers, Boston, 2005.
The author presents several methods for outlier detection, while distinguishing between univariate versus multivariate techniques and parametric versus nonparametric procedures. In the presence of outliers, special attention should be taken to assure the robustness of the used estimators. Outlier detection for data mining is often based on distance measures, clustering, and spatial methods.
Kennedy, R. L. et al.,
Solving Data Mining Problems through Pattern Recognition
, Prentice Hall, Upper Saddle River, NJ, 1998.
The book takes a practical approach to overall data-mining project development. The rigorous, multistep methodology includes defining the data set; collecting, preparing, and preprocessing data; choosing the appropriate technique and tuning the parameters; and training, testing, and troubleshooting.
Weiss, S. M., N. Indurkhya,
Predictive Data Mining: A Practical Guide
, Morgan Kaufman Publishers, San Francisco, CA, 1998.
This book focuses on the data-preprocessing phase in successful data-mining applications. Preparation and organization of data and development of an overall strategy for data mining are not only time-consuming processes, but also fundamental requirements in real-world data mining. The simple presentation of topics with a large number of examples is an additional strength of the book.
3
DATA REDUCTION
Chapter Objectives
- Identify the differences in dimensionality reduction based on features, cases, and reduction of value techniques.
- Explain the advantages of data reduction in the preprocessing phase of a data-mining process.
- Understand the basic principles of feature-selection and feature-composition tasks using corresponding statistical methods.
- Apply and compare entropy-based technique and principal component analysis (PCA) for feature ranking.
- Understand the basic principles and implement ChiMerge and bin-based techniques for reduction of discrete values.
- Distinguish approaches in cases where reduction is based on incremental and average samples.
For small or moderate data sets, the preprocessing steps mentioned in the previous chapter in preparation for data mining are usually enough. For really large data sets, there is an increased likelihood that an intermediate, additional step—data reduction—should be performed prior to applying the data-mining techniques. While large data sets have the potential for better mining results, there is no guarantee that they will yield better knowledge than small data sets. Given multidimensional data, a central question is whether it can be determined, prior to searching for all data-mining solutions in all dimensions, that the method has exhausted its potential for mining and discovery in a reduced data set. More commonly, a general solution may be deduced from a subset of available features or cases, and it will remain the same even when the search space is enlarged.
The main theme for simplifying the data in this step is dimension reduction, and the main question is whether some of these prepared and preprocessed data can be discarded without sacrificing the quality of results. There is one additional question about techniques for data reduction: Can the prepared data be reviewed and a subset found in a reasonable amount of time and space? If the complexity of algorithms for data reduction increases exponentially, then there is little to gain in reducing dimensions in big data. In this chapter, we will present basic and relatively efficient techniques for dimension reduction applicable to different data-mining problems.
3.1 DIMENSIONS OF LARGE DATA SETS
The choice of data representation and selection, reduction, or transformation of features is probably the most important issue that determines the quality of a data-mining solution. Besides influencing the nature of a data-mining algorithm, it can determine whether the problem is solvable at all, or how powerful the resulting model of data mining is. A large number of features can make available samples of data relatively insufficient for mining. In practice, the number of features can be as many as several hundred. If we have only a few hundred samples for analysis, dimensionality reduction is required in order for any reliable model to be mined or to be of any practical use. On the other hand, data overload, because of high dimensionality, can make some data-mining algorithms non-applicable, and the only solution is again a reduction of data dimensions. For example, a typical classification task is to separate healthy patients from cancer patients, based on their gene expression “profile.” Usually fewer than 100 samples (patients’ records) are available altogether for training and testing. But the number of features in the raw data ranges from 6000 to 60,000. Some initial filtering usually brings the number of features to a few thousand; still it is a huge number and additional reduction is necessary. The three main dimensions of preprocessed data sets, usually represented in the form of flat files, are
columns
(features),
rows
(cases or samples), and
values
of the features.
Therefore, the three basic operations in a data-reduction process are delete a column, delete a row, and reduce the number of values in a column (smooth a feature). These operations attempt to preserve the character of the original data by deleting data that are nonessential. There are other operations that reduce dimensions, but the new data are unrecognizable when compared with the original data set, and these operations are mentioned here just briefly because they are highly application-dependent. One approach is the replacement of a set of initial features with a new composite feature. For example, if samples in a data set have two features, person height and person weight, it is possible for some applications in the medical domain to replace these two features with only one, body mass index, which is proportional to the quotient of the initial two features. Final reduction of data does not reduce the quality of results; in some applications, the results of data mining are even improved.
In performing standard data-reduction operations (deleting rows, columns, or values) as a preparation for data mining, we need to know what we gain and/or lose with these activities. The overall comparison involves the following parameters for analysis:
1.
Computing Time.
Simpler data, a result of the data-reduction process, can hopefully lead to a reduction in the time taken for data mining. In most cases, we cannot afford to spend too much time on the data-preprocessing phases, including a reduction of data dimensions, although the more time we spend in preparation the better the outcome.
2.
Predictive/Descriptive Accuracy.
This is the dominant measure for most data-mining models since it measures how well the data are summarized and generalized into the model. We generally expect that by using only relevant features, a data-mining algorithm can learn not only faster but also with higher accuracy. Irrelevant data may mislead a learning process and a final model, while redundant data may complicate the task of learning and cause unexpected data-mining results.
3.
Representation of the Data-Mining Model.
The simplicity of representation, obtained usually with data reduction, often implies that a model can be better understood. The simplicity of the induced model and other results depends on its representation. Therefore, if the simplicity of representation improves, a relatively small decrease in accuracy may be tolerable. The need for a balanced view between accuracy and simplicity is necessary, and dimensionality reduction is one of the mechanisms for obtaining this balance.
It would be ideal if we could achieve reduced time, improved accuracy, and simplified representation at the same time, using dimensionality reduction. More often than not, however, we gain in some and lose in others, and balance between them according to the application at hand. It is well known that no single data-reduction method can be best suited for all applications. A decision about method selection is based on available knowledge about an application (relevant data, noise data, meta-data, correlated features), and required time constraints for the final solution.
Algorithms that perform all basic operations for data reduction are not simple, especially when they are applied to large data sets. Therefore, it is useful to enumerate the desired properties of these algorithms before giving their detailed descriptions. Recommended characteristics of data-reduction algorithms that may be guidelines for designers of these techniques are as follows:
1.
Measurable Quality.
The quality of approximated results using a reduced data set can be determined precisely.
2.
Recognizable Quality.
The quality of approximated results can be easily determined at run time of the data-reduction algorithm, before application of any data-mining procedure.
3.
Monotonicity.
The algorithms are usually iterative, and the quality of results is a nondecreasing function of time and input data quality.
4.
Consistency.
The quality of results is correlated with computation time and input data quality.
5.
Diminishing Returns.
The improvement in the solution is large in the early stages (iterations) of the computation, and it diminishes over time.
6.
Interruptability.
The algorithm can be stopped at any time and provide some answers.
7.
Preemptability.
The algorithm can be suspended and resumed with minimal overhead.
3.2 FEATURE REDUCTION
Most of the real-world data mining applications are characterized by high-dimensional data, where not all of the features are important. For example, high-dimensional data (i.e., data sets with hundreds or even thousands of features) can contain a lot of irrelevant, noisy information that may greatly degrade the performance of a data-mining process. Even state-of-the-art data-mining algorithms cannot overcome the presence of a large number of weakly relevant and redundant features. This is usually attributed to the “curse of dimensionality,” or to the fact that irrelevant features decrease the signal-to-noise ratio. In addition, many algorithms become computationally intractable when the dimensionality is high.
Data such as images, text, and multimedia are high-dimensional in nature, and this dimensionality of data poses a challenge to data-mining tasks. Researchers have found that reducing the dimensionality of data results in a faster computation while maintaining reasonable accuracy. In the presence of many irrelevant features, mining algorithms tend to overfit the model. Therefore, many features can be removed without performance deterioration in the mining process.
When we are talking about data quality and improved performances of reduced data sets, we can see that this issue is not only about noisy or contaminated data (problems mainly solved in the preprocessing phase), but also about irrelevant, correlated, and redundant data. Recall that data with corresponding features are not usually collected solely for data-mining purposes. Therefore, dealing with relevant features alone can be far more effective and efficient. Basically, we want to choose features that are relevant to our data-mining application in order to achieve maximum performance with minimum measurement and processing effort. A feature-reduction process should result in
1.
less data so that the data-mining algorithm can learn faster;
2.
higher accuracy of a data-mining process so that the model can generalize better from the data;
3.
simple results of the data-mining process so that they are easier to understand and use; and
4.
fewer features so that in the next round of data collection, savings can be made by removing redundant or irrelevant features.
Let us start our detailed analysis of possible column-reduction techniques, where features are eliminated from the data set based on a given criterion. To address the curse of dimensionality, dimensionality-reduction techniques are proposed as a data-preprocessing step. This process identifies a suitable low-dimensional representation of original data. Reducing the dimensionality improves the computational efficiency and accuracy of the data analysis. Also, it improves comprehensibility of a data-mining model. Proposed techniques are classified as supervised and unsupervised techniques based on the type of learning process. Supervised algorithms need a training set with the output class label information to learn the lower dimensional representation according to some criteria. Unsupervised approaches project the original data to a new lower dimensional space without utilizing the label (class) information. Dimensionality-reduction techniques function either by transforming the existing features to a new reduced set of features or by selecting a subset of the existing features. Therefore, two standard tasks are associated with producing a reduced set of features, and they are classified as:
1.
Feature Selection.
Based on the knowledge of the application domain and the goals of the mining effort, the human analyst may select a subset of the features found in the initial data set. The process of feature selection can be manual or supported by some automated procedures.
Roughly speaking, feature-selection methods are applied in one of three conceptual frameworks: the
filter model
, the
wrapper model
, and
embedded methods
. These three basic families differ in how the learning algorithm is incorporated in evaluating and selecting features. In the filter model the selection of features is done as a preprocessing activity, without trying to optimize the performance of any specific data-mining technique directly. This is usually achieved through an (ad hoc) evaluation function using a search method in order to select a subset of features that maximizes this function. Performing an exhaustive search is usually intractable due to the large number of initial features. Therefore, different methods may apply a variety of search heuristics. Wrapper methods select features by “wrapping” the search around the selected learning algorithm and evaluate feature subsets based on the learning performance of the data-mining technique for each candidate feature subset. The main drawback of this approach is its computational complexity. Main characteristics of both approaches are given in Figure
3.1
. Finally, embedded methods incorporate feature search and the learning algorithm into a single optimization problem formulation. When the number of samples and dimensions becomes very large, the filter approach is usually a choice due to its computational efficiency and neutral bias toward any learning methodology.
2.
Feature Extraction/Transformation.
There are transformations of data that can have a surprisingly strong impact on the results of data-mining methods. In this sense, the composition and/or transformation of features is a greater determining factor in the quality of data-mining results. In most instances, feature composition is dependent on knowledge of the application, and an interdisciplinary approach to feature composition tasks produces significant improvements in the preparation of data. Still, some general purpose techniques, such as PCA, are often used and with great success.
Feature selection is typically preferred over extraction/transformation when one wishes to keep the original meaning of the features and wishes to determine which of those features are important. Moreover, once features are selected, only those features need to be calculated or collected, whereas in transformation-based methods all input features are still needed to obtain the reduced dimension.
