Data Mining (15 page)
Authors: Mehmed Kantardzic

Figure 3.1.
Feature-selection approaches. (a) Filter model; (b) wrapper model.

3.2.1 Feature Selection
In data mining, feature selection, also known as variable selection, feature reduction, attribute selection, or variable subset selection, is a set of techniques that select a subset of relevant features for building robust learning models by removing most irrelevant and redundant features from the data. The objective of feature selection is threefold: improving the performance of a data-mining model, providing a faster and more cost-effective learning process, and providing a better understanding of the underlying process that generates the data. Feature-selection algorithms typically fall into two categories:
feature ranking
and
subset selection
. Feature ranking ranks all features by a specified metric and eliminates all features that do not achieve an adequate score. Subset selection, on the other hand, searches the set of all features for the optimal subset where features in the selected subset are not ranked. We have to be aware that different feature-selection methods may give different reduced feature sets.
In the feature-ranking algorithm, one can expect a ranked list of features that are ordered according to a specific evaluation measure. A measure can be based on accuracy of available data, consistency, information content, distances between samples, and finally, statistical dependencies between features. These algorithms do not tell you what the minimum set of features for further analysis is; they indicate only the relevance of a feature compared with others. Minimum-subset algorithms, on the other hand, return a minimum feature subset and no differences are made among features in the subset—all have the same ranking. The features in the subset are relevant for the mining process; the others are irrelevant. In both types of algorithms, it is important to establish a feature-evaluation scheme: the way in which the features are evaluated and then ranked, or added to the selected subset.
Feature selection in general can be viewed as a search problem, with each state in the search space specifying a subset of the possible features. If, for example, a data set has three features, {A
1
, A
2
, A
3
}, and in the process of selecting features, the presence of a feature is coded with 1 and its absence with 0, then there should be a total of 2
3
reduced-feature subsets coded with {0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, {1, 1, 0}, {1, 0, 1}, {0, 1, 1}, and {1, 1, 1}. The problem of feature selection is relatively trivial if the search space is small, since we can analyze all subsets in any order and a search will get completed in a short time. However, the search space is usually not small. It is 2
N
where the number of dimensions N in typical data-mining applications is large (N > 20). This makes the starting point and the search strategy very important. An exhaustive search of all subsets of features very often is replaced with some heuristic search procedures. With knowledge of the problem, these procedures find near-optimal subsets of features that further improve the quality of the data-mining process.
The objective of feature selection is to find a subset of features with data-mining performances comparable to the full set of features. Given a set of features m, the number of subsets to be evaluated as candidates for column reduction is finite, but still very large for iterative analysis through all cases. For practical reasons, an optimal search is not feasible, and simplifications are made to produce reasonable, acceptable, and timely results. If the reduction task is to create a subset, one possibility—the so-called bottom-up approach—starts with an empty set, and fills it in by choosing the most relevant features from the initial set of features. This process is based on some heuristic criteria for a feature evaluation. The top-down approach, on the other hand, begins with a full set of original features and then removes one-by-one those that are shown as irrelevant based on the selected heuristic evaluation measure. Additional approximations to the optimal approach are
1.
to examine only promising subsets of features where promising subsets are usually obtained heuristically—this provides enough room for exploration of competing alternatives;
2.
to substitute computationally simple distance measures for the error measures—this approximation will reduce the computation time yet give satisfactory results for comparison of subset alternatives;
3.
to select features based only on subsets of large amounts of data, but the subsequent steps of data mining will be applied on the whole set.
The application of feature selection and reduction of data dimensionality may be used in all phases of the data-mining process for successful knowledge discovery. It has to be started in the preprocessing phase, but, on many occasions, feature selection and reduction is a part of the data-mining algorithm, even if it is applied in postprocessing for better evaluation and consolidation of obtained results.
Let us return to the promising subsets of features. One possible technique for feature selection is based on comparison of
means
and
variances
. To summarize the key characteristics of the distribution of values for a given feature, it is necessary to compute the mean value and the corresponding variance. The main weakness in this approach is that the distribution for the feature is not known. If it is assumed to be a normal curve, the statistics can work out very well, but this may in fact be a poor assumption. Without knowing the shape of the distribution curve, the means and variances are viewed as heuristics for feature selection, not exact, mathematical modeling tools.
In general, if one feature describes different classes of entities, samples of two different classes can be examined. The means of feature values are normalized by their variances and then compared. If the means are far apart, interest in a feature increases; it has potential, in terms of its use in distinguishing between two classes. If the means are indistinguishable, interest wanes in that feature. It is a heuristic, nonoptimal approach to feature selection, but it is consistent with practical experience in many data-mining applications in the triage of features. Next, equations formalize the test, where A and B are sets of feature values measured for two different classes, and n
1
and n
2
are the corresponding number of samples:

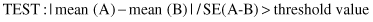
The mean of a feature is compared in both classes without taking into consideration relationship to other features. In this approach to feature selection, we assumed a priori that the given feature is independent of the others. A comparison of means is a natural fit to classification problems. For the purposes of feature selection, a regression problem can be considered as a pseudo-classification problem. For k classes, k pairwise comparisons can be made, comparing each class with its complement. A feature is retained if it is significant for any of the pairwise comparisons.
We can analyze this approach in feature selection through one example. A simple data set is given in Table
3.1
with two input features X and Y, and an additional output feature C that classifies samples into two classes, A and B. It is necessary to decide whether the features X and Y are candidates for reduction or not. Suppose that the threshold value of the applied test is 0.5.
TABLE 3.1.
Dataset with Three Features
| X | Y | C |
| 0.3 | 0.7 | A |
| 0.2 | 0.9 | B |
| 0.6 | 0.6 | A |
| 0.5 | 0.5 | A |
| 0.7 | 0.7 | B |
| 0.4 | 0.9 | B |
First, we need to compute a mean value and a variance for both classes and both features X and Y. The analyzed subsets of the feature’s values are

and the results of applied tests are