For the Love of Physics (15 page)
Read For the Love of Physics Online
Authors: Walter Lewin
Tags: #Biography & Autobiography, #Science & Technology, #Science, #General, #Physics, #Astrophysics, #Essays

After these rays of sunlight refract, reflect, and refract again on their way out of the raindrop, they have pretty much reversed direction. Key to why we see rainbows is that red light exits the raindrop at angles that are
always smaller
than about 42 degrees from the original direction of the sunlight entering the drop. And this is the same for all raindrops, because the Sun for all practical purposes is infinitely far away. The angle at which the red light exits can be anything between 0 degrees and 42 degrees but never more than 42 degrees, and this maximum angle is different for each of the different colors. For violet light, the maximum angle is about 40 degrees. These different maximum angles for each color account for the stripes of colors in the rainbow.

There is an easy way to spot a rainbow when conditions are right. As seen in the following figure, if I trace a line from the Sun through my head to the far end of my shadow on the ground, that line is precisely parallel to the direction from the Sun to the raindrops. The higher the Sun in the sky, the steeper this line will be, and the shorter my shadow. The converse is also the case. This line, from the Sun, through my head, to the shadow of my head on the ground, we will call the imaginary line. This line is very important as it will tell you where in the sky you should look to see the rainbow.
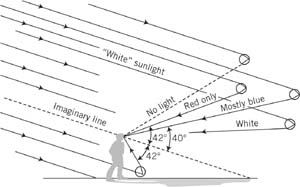
All raindrops at 42 degrees from the “imaginary line” will be red. Those at 40 degrees will be blue. raindrops at angles smaller than 40 degrees will be white (like the sunlight). We will see no light from drops at angles larger than 42 degrees (see text).
If you look about 42 degrees away from that imaginary line—it doesn’t matter whether it’s straight up, to the right, or to the left—that’s where you will see the red band of the rainbow. At about 40 degrees away from it—up, right, or left—you will see the violet band of the rainbow. But the truth is that violet is hard to see in a rainbow, so you’ll see the blue much more easily. Therefore we’ll just say blue from now on. Aren’t these the same angles I mentioned earlier, talking about the maximum angles of the light leaving the raindrop? Yes, and it’s no accident. Look again at the figure.
What about the blue band in the rainbow? Well, remember its magic number is just about 40 degrees, 2 degrees less than the red band. So blue light can be found refracting, reflecting, and refracting out of
different raindrops
at a
maximum
angle of 40 degrees. Thus we see blue light 40 degrees away from the imaginary line. Since the 40-degree band is closer to the imaginary line than the 42-degree band, the blue band will always be on the
inside
of the red band of the rainbow. The other colors making up the bow—orange, yellow, green—are found between the red and blue bands. For more about this you can take a look at my lecture on rainbows online, at
http://ocw.mit.edu/courses/physics/8-03-physics-iii-vibrations-and-waves-fall-2004/video-lectures/lecture-22/
.
Now you might wonder, at the maximum angle for blue light, are we seeing only blue light? After all, red light can also emerge at 40 degrees, as it is smaller than 42 degrees. If you’ve asked this question, more power to you—it’s a very astute one. The answer is that at the maximum angle for any given color, that color dominates all other colors. With red, though, because its angle is the highest, it
is
the only color.
Why is the rainbow a bow and not a straight line? Go back to that imaginary line from your eyes to the shadow of your head, and the magic number 42 degrees. When you measure 42 degrees—in all directions—away from the imaginary line, you are tracing an arc of color. But you know that not all rainbows are full arcs—some are just little pieces in the sky. That happens when there aren’t enough raindrops in all directions in the sky or when certain parts of the rainbow are in the shadow of obstructing clouds.
There’s another important aspect to this collaboration between the Sun, the raindrops, and your eyes, and once you see it, you’ll understand lots more about why rainbows—natural as well as artificial—are the way they are. For example, why are some rainbows enormous, while others just hug the horizon? And what accounts for the rainbows you sometimes see in pounding surf, or in fountains, waterfalls, or the spray of your garden hose?
Let’s go back to the imaginary line that runs from your eyes to the shadow of your head. This line starts at the Sun, behind you, and extends to the ground. However, in your mind, you can extend this line as far as you want, even much farther than the shadow of your head. This imaginary line is very useful, as you can imagine it going through the center (called the antisolar point) of a circle, on the circumference of which is the rainbow. This circle represents where the rainbow would form if the surface of Earth didn’t get in its way. Depending upon how high in the sky the Sun is, a rainbow will also be lower or higher above the horizon. When the Sun is very high, the rainbow may only just peek above the horizon, whereas late in the afternoon just before sunset, or early in the morning just around sunrise, when the Sun is low in the sky and when your shadow is long, then a rainbow may be enormous, reaching halfway up into the sky. Why halfway? Because the maximum angle it can be over the horizon is 42 degrees, or close to 45 degrees, which is half of the 90 degrees that would be right overhead.
So how can you go rainbow hunting? First of all, trust your instincts about when a rainbow might form. Most of us tend to have a good intuitive sense of that: those times when the Sun is shining just before a rainstorm, or when it comes out right after one. Or when there’s a light shower and the sunlight can still reach the raindrops.
When you feel one coming on, here’s what you do. First, turn your back to the Sun. Then locate the shadow of your head, and look about 42 degrees in any direction away from the imaginary line. If there’s enough sunlight, and if there are enough raindrops, the collaboration will work and you will see a colorful bow.
Suppose you cannot see the Sun at all—it’s somehow hidden by clouds or buildings, but it’s clearly shining. As long as there are no clouds between the Sun and the raindrops, you still ought to be able to see a rainbow. I can see rainbows in the late afternoon from my living room facing east when I cannot see the Sun that is in the west. Indeed, most of the time you don’t need the imaginary line and the 42-degree trick to spot a rainbow, but there is one situation where paying attention to both can make a big difference. I love to walk on the beaches of Plum Island off the Massachusetts coast. Late in the afternoon the sun is in the west and the ocean is to the east. If the waves are high enough and if they make lots of small water drops, these droplets act like raindrops and you can see two small pieces of the rainbow: one piece at about 42 degrees to the left of the imaginary line and a second piece about 42 degrees to the right. These rainbows only last for a split second, so it’s a huge help in spotting them if you know where to look in advance. Since there are always more waves coming, you will always succeed if you can be patient enough. More about this later in this chapter.
Here is another thing you can try to look for, the next time you spot a rainbow. Remember our discussion of the maximum angle at which certain light can refract out of the raindrop? Well, even though you will see blue, or red, or green from certain raindrops, raindrops themselves cannot be so choosy: they refract, reflect, and refract lots of light at
less
than a 40-degree angle too. This light is a mixture of all the different colors at roughly equal intensities, which we see as white light. That’s why, inside the blue band of a rainbow, the sky is very bright and white. At the same time,
none
of the light that refracts, reflects, and refracts again can exit raindrops beyond the 42-degree angle, so the sky just outside the bow is darker than inside the bow. This effect is most visible if you compare the brightness of the sky on either side of the rainbow. If you’re not specifically looking for it, you probably won’t even notice it. There are excellent images of rainbows in which you can see this effect on the Atmospheric Optics website, at
www.atoptics.co.uk
.
Once I began explaining rainbows to my students, I realized just how
rich a subject they are—and how much more I had to learn. Take double rainbows, which you’ve probably seen from time to time. In fact, there are almost always two rainbows in the sky: the so-called primary bow, the one I’ve been discussing, and what we call the secondary bow.
If you’ve seen a double rainbow, you’ve probably noticed that the secondary bow is much fainter than the primary bow. You probably
haven’t
noticed, though, that the order of colors in the secondary bow is blue on the outside and red on the inside, the reverse of that in the primary. There is an excellent photograph of a double rainbow in this book’s photo insert.
In order to understand the origin of the secondary bow, we have to go back to our ideal raindrop—remember, of course, that it actually takes zillions of drops to make up a secondary rainbow as well. Some of the light rays entering the drops reflect just once; others reflect twice before exiting. While light rays entering any given raindrop can reflect many times inside it, the primary bow is only created by those that reflect
once.
The secondary bow, on the other hand, is created only by those that reflect
twice
inside before refracting on the way out. This extra bounce inside the raindrop is the reason the colors are reversed in the secondary bow.
The reason the secondary bow is in a different position from the primary bow—always outside it—is that twice-reflected red rays exit the drop at angles always
larger
(yes, larger) than about 50 degrees, and the twice-reflected blue rays come out at angles always larger than about 53 degrees. You therefore need to look for the secondary bow about 10 degrees
outside
the primary bow. The reason that the secondary bow is much fainter is that so much less light reflects inside the raindrops twice than reflects once, so there’s less light to make the bow. This is, of course, why it can be hard to see the secondary bow, but now that you know they often accompany primary rainbows, and where to look for them, I’m confident you’ll see lots more. I also suggest that you spend a few minutes on the Atmospheric Optics website.
Now that you know what makes rainbows, you can perform a little
optical magic in your own backyard or on your driveway or even on the sidewalk, with just a garden hose. But because you can manipulate the raindrops, and they are physically close to you, there are a couple of big differences. For one thing, you can make a rainbow even when the Sun is high in the sky. Why? Because you can make raindrops between you and your shadow on the ground, something that rarely happens naturally. As long as there are raindrops that the sunlight can reach, there can be rainbows. You may have done this already, but perhaps not as purposefully.
If you have a nozzle on the end of the hose, adjust it to a fine spray, so the droplets are quite small, and when the Sun is high in the sky, point the nozzle toward the ground and start spraying. You cannot see the entire circle all at once, but you will see pieces of the rainbow. As you continue moving the nozzle in a circle, piece by piece you will see the entire circle of the rainbow. Why do you have to do it this way? Because you don’t have eyes in the back of your head!
You will see red at about 42 degrees from the imaginary line, the inside edge of the circular bow will be blue, and inside the bow you will see white light. I love performing this little act of creation while watering my garden, and it’s especially satisfying to be able to turn all the way around and make a complete 360-degree rainbow. (The Sun, of course, will then not always be behind you.)

