From Eternity to Here (18 page)

On the other hand, you could distort the total amount of time experienced along your world line as compared to the world lines of other people. In a Newtonian universe even that wouldn’t be possible, as time is universal and every world line connecting the same two events experiences the same elapsed time. But in special relativity we can affect the elapsed time by moving through space. Unaccelerated motion gives us the longest time between events; so if you want to get to the future quickly (from your perspective), you just have to move on a highly non-straight path through spacetime. You could zip out on a rocket near the speed of light and then return; or, given sufficient fuel, you could just fly around in circles at ultra-high speed, never straying very far from your starting point in space. When you stopped and exited your spaceship, besides being dizzy you would have “traveled into the future”; more accurately, you would have experienced less time along your world line than was experienced by anyone who stayed behind. Traveling to the future is easy, and getting there more quickly is just a technology problem, not something that conflicts with the fundamental laws of physics.

But you might want to come back, and that’s where the challenge lies. The problems with traveling through time arise when we contemplate traveling to the
past
.

CHEATING SPACETIME

Lessons learned from watching
Superman
movies notwithstanding, traveling backward in time is not a matter of reversing the rotation of the Earth. Spacetime itself has to cooperate. Unless, of course, you cheat, by moving faster than the speed of light.

In a Newtonian universe, traveling backward in time is simply out of the question. World lines extend through a spacetime that is uniquely divided into three-dimensional moments of equal time, and the one unbreakable rule is that they must never double back and return to the past. In special relativity, things aren’t much better. Defining “moments of equal time” across the universe is highly arbitrary, but at every event we are faced with the restrictions enforced by light cones. If we are made of ordinary stuff, confined to move from each event forward into the interior of its light cone, there is no hope of traveling backward in time; in a spacetime diagram, we are doomed to march relentlessly upward.

Things would be a little bit more interesting if we were made of non-ordinary stuff. In particular, if we were made of
tachyons
—particles that always move faster than light. Sadly, we are not made of tachyons, and there are good reasons to believe that tachyons don’t even exist. Unlike ordinary particles, tachyons are forced to always travel outside the light cone. In special relativity, whenever we move outside the light cone, from somebody’s point of view we’re also moving backward in time. More important, the light cones are the only structure defined on spacetime in relativity; there is no separate notion of “space at one moment of time.” So if a particle can start at some event where you are momentarily located and move outside your light cone (faster than light), it can necessarily move into the past from your point of view. There’s nothing to stop it.

Tachyons, therefore, can apparently do something scary and unpredictable: “start” from an event on the world line of some ordinary (slower-than-light) object, defined by some position in space and some moment in time, and travel on a path that takes them to a
previous
point on the same world line. If you had a flashlight that emitted tachyons, you could (in principle) construct an elaborate series of mirrors by which you could send signals in Morse code to yourself in the past. You could warn your earlier self not to eat the shrimp in that restaurant that one time, or to go on that date with the weirdo from the office, or to sink your life savings into
Pets.com
stock.

Figure 22:
If tachyons could exist, they could be emitted by ordinary objects and zip around to be absorbed in the past. At every event along its trajectory, the tachyon moves outside the light cone.

Clearly, the possibility of travel backward in time raises the possibility of paradoxes, which is unsettling. There is a cheap way out: Notice that tachyons don’t seem to exist, and declare that they are simply incompatible with the laws of physics.
⁷⁷
That is both fruitful and accurate, at least as far as special relativity is concerned. When curved spacetime gets into the game, things become more interesting.

CIRCLES IN TIME

For those of us who are not made of tachyons, our trajectories through spacetime are limited by the speed of light. From whatever event defines our current location, we necessarily move “forward in time,” toward some other event inside our light cone—in technical jargon, we move on a timelike path through spacetime. This is a local requirement, referring only to features of our neighborhood of the universe. But in general relativity, spacetime is curved. That means light cones in our neighborhood may be tilted with respect to those far away. It’s that kind of tilting that leads to black holes.

But imagine that, instead of light cones tilting inward toward a singularity and creating a black hole, we had a spacetime in which light cones tilted around a circle, as shown in Figure 23. Clearly this would require some sort of extremely powerful gravitational field, but we’re letting our imaginations roam. If spacetime were curved in that way, a remarkable thing would happen: We could travel on a timelike path, always moving forward into our future light cone, and yet eventually meet ourselves at some moment in our past. That is, our world line could describe a closed loop in space, so that it intersected itself, bringing us at one moment in our lives face-to-face with ourselves at some other moment.

Figure 23:
In curved spacetime, we can imagine light cones tilting around in a circle, creating closed timelike curves.

Such a world line—always moving forward in time from a local perspective, but managing to intersect itself in the past—is a
closed timelike curve
, or CTC. That’s what we really mean when we talk about a “time machine” in general relativity. To actually move along the closed timelike curve would involve ordinary travel through spacetime, on a spaceship or something even more mundane—perhaps even sitting “motionless” in your chair. It’s the curvature of spacetime itself that brings you into contact with your own past. This is a central feature of general relativity that will become important later on when we return to the origin of the universe and the problem of entropy: Spacetime is not stuck there once and for all, but can change (and even come into or pop out of existence) in response to the effects of matter and energy.

It’s not difficult to find spacetimes in general relativity that include closed timelike curves. All the way back in 1949, mathematician and logician Kurt Gödel found a solution to Einstein’s equation that described a “spinning” universe, which contains closed timelike curves passing through every event. Gödel was friends with Einstein in his later years at the Institute for Advanced Study in Princeton, and the idea for his solution arose in part from conversations between the two men.
⁷⁸
In 1963, New Zealand mathematician Roy Kerr found the exact solution for a rotating black hole; interestingly, the singularity takes the form of a rapidly spinning ring, the vicinity of which is covered by closed timelike curves.
⁷⁹
And in 1974, Frank Tipler showed that an infinitely long, rotating cylinder of matter would create closed timelike curves around it, if the cylinder were sufficiently dense and rotating sufficiently rapidly.
⁸⁰

But you don’t have to work nearly so hard to construct a spacetime with closed timelike curves. Consider good old garden-variety flat spacetime, familiar from special relativity. But now imagine that the timelike direction (as defined by some particular unaccelerated observer) is a
circle
, rather than stretching on forever. In such a universe, something that moved forward in time would find itself coming back to the same moment in the universe’s history over and over. In the Harold Ramis movie
Groundhog Day
, Bill Murray’s character keeps waking up every morning to experience the exact same situations he had experienced the day before. The circular-time universe we’re imagining here is something like that, with two important exceptions: First, it would be truly identical every day, including the actions of the protagonist himself. And second, there would not be any escape. In particular, winning the love of Andie MacDowell would not save you.

The circular-time universe isn’t just an amusing playground for filmmak ers; it’s an exact solution to Einstein’s equation. We know that, by choosing some unaccelerated reference frame, we can “slice” four-dimensional flat spacetime into three-dimensional moments of equal time. Take two such slices: say, midnight February 2, and midnight February 3—two moments of time that extend throughout the universe (in this special case of flat spacetime, in this particular reference frame). Now take just the one-day’s-worth of spacetime that is between those slices, and throw everything else away. Finally,
identify
the beginning time with the final time. That is, make a rule that says whenever a world line hits a particular point in space on February 3, it instantly reemerges at the same point in space back on February 2. At heart, it’s nothing more than rolling up a piece of paper and taping together opposite sides to make a cylinder. At every event, even at midnight when we’ve identified different slices, everything looks perfectly smooth and spacetime is flat—time is a circle, and no point on a circle is any different than any other point. This spacetime is rife with closed timelike curves, as illustrated in Figure 24. It might not be a realistic universe, but it demonstrates that the rules of general relativity alone do not prohibit the existence of closed timelike curves.

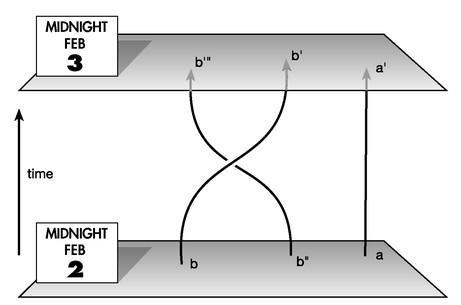
Figure 24:
A circular-time universe, constructed by identifying two different moments in flat spacetime. Two closed timelike curves are shown: one that loops through only once before closing, from (a) to (a‘), and another that loops twice, from (b) to (b’) to (b“) to (b’ ”).

THE GATE INTO YESTERDAY

There are two major reasons why most people who have given the matter a moment’s thought would file the possibility of time travel under “Science Fiction,” not “Serious Research.” First, it’s hard to see how to actually create a closed timelike curve, although we’ll see that some people have ideas. But second, and more fundamentally, it’s hard to see how the notion could make sense. Once we grant the possibility of traveling into our own past, it’s just too easy to invent nonsensical or paradoxical situations.

To fix our ideas, consider the following simple example of a time machine: the gate into yesterday. (“Gate into tomorrow” would be equally accurate—just go the other way.) We imagine there is a magical gate, standing outside in a field. It’s a perfectly ordinary gate in every way, with one major exception: When you walk through from what we’ll call “the front,” you emerge in the same field on the other side, but
one day earlier
—at least, from the point of view of the “background time” measured by outside observers who don’t ever step through the gate. (Imagine fixed clocks standing in the field, never passing through the gate, synchronized in the rest frame of the field itself.) Correspondingly, when you walk through the back side of the gate, you emerge through the front one day later than when you left.