Full House (12 page)

I do not believe that rulemakers sit down with pencil and paper, trying to divine a change that will bring mean batting averages back to an ideal. Rather, the prevailing powers have a sense of what constitutes proper balance between hitting and pitching, and they jiggle minor factors accordingly (height of mound, size of strike zone, permissible and impermissible alterations of the bat, including pine tar and corking)—in order to assure stability within a system that has not experienced a single change of fundamental rules and standards for more than a century.
But the rulemakers do not (and probably cannot) control amounts of variation around their roughly stabilized mean. I therefore set out to test my hypothesis—based on the alternate construction of reality as the full house of "variation in a system" rather than "a thing moving somewhere"—that 0.400 hitting (as the right tail in a system of variation rather than a separable thing-in-itself) might have disappeared as a consequence of shrinking variation around this stable mean.
I did my first study "on the cheap" when I was recovering from serious illness in the early 1980s (see chapter 4). I propped myself up in bed with the only book in common use that is thicker than the Manhattan telephone directory—The Baseball Encyclopedia (New York, Macmillan). I decided to treat the mean batting average for the five best and five worst players in each year as an acceptable measure of achievement at the right and left tails of the bell curve for batting averages. I then calculated the difference between these five highest and the league average (and also between the five lowest and the league average) for each year since the beginning of major league baseball, in 1876. If the difference between best and average (and worst and average) declines through time, then we will have a rough measurement for the shrinkage of variation.
The five best are easily identified, for the Encyclopedia lists them in yearly tables of highest achievement. But nobody bothers to memorialize the five worst, so I had to go through the rosters, man by man, looking for the five lowest averages among regular players with at least two at-bats per game over a full season. I present the results in Figure 15—a clear confirmation of my hypothesis, as variation shrinks systematically and symmetrically, bringing both right and left tails ever closer to the stable mean through time. Thus, the disappearance of 0.400 hitting occurred because the bell curve for batting averages has become skinnier over the years, as extreme values at both right and left tails of the distribution get trimmed and shaved. To understand the extinction of 0.400 hitting, we must ask why variation declined in this particular pattern.
Several years later I redid the study by a better, albeit far more laborious, method of calculating the conventional measure of total variation— the standard deviation—for all regular players in each year (three weeks at the computer for my research assistant—and did he ever relish the break from measuring snails!—rather than several enjoyable personal hours propped up in bed with the Baseball Encyclopedia).
The standard deviation is a statistician’s basic measure of variation. The calculated value for each year records the spread of the entire bell curve, measured (roughly) as the average departure of players from the mean—thus giving us, in a single number, our best assessment of the full range of variation. To compute the standard deviation, you take (in this case) each individual batting average and subtract from it the league average for that year. You then square each value (multiply it by itself) in order to eliminate negative numbers for batting averages below the mean (for a negative times a negative yields a positive number). You then add up all these values and divide them by the total number of players, giving an average squared deviation of individual players from the mean. Finally, you take the square root of this number to obtain the average, or standard, deviation itself. The higher the value of the standard deviation, the more extensive, or spread out, the variation.
6
Calculation by standard deviation gives a more detailed account of the shrinkage of variation in batting averages through time—see Figure 16, which plots the changes in standard deviation year by year, with no averaging over decades or other intervals. My general hypothesis is confirmed again: variation decreases steadily through time, leading to the disappearance of 0.400 hitting as a consequence of shrinkage at the right tail of the distribution. But, using this preferable, and more powerful, method of standard deviations, we can discern some confirming subtleties in the pattern of decrease that our earlier analysis missed. We note in particular that, while standard deviations have been dropping steadily and irreversibly, the decline itself has decelerated over the years as baseball has stabilized—rapidly during the nineteenth century, more slowly during the twentieth, and reaching a plateau by about 1940.
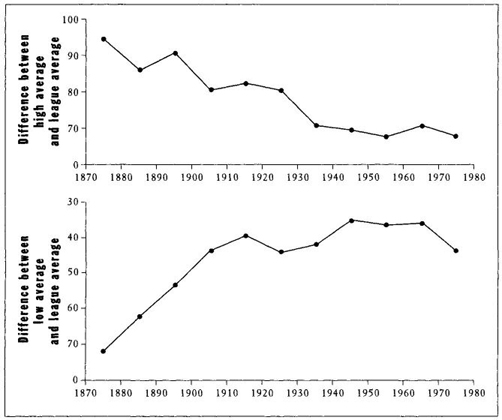
FIGURE 15 Declining differences between highest and lowest batting averages and league means throughout the history of baseball.
Please pardon a bit of crowing, but I was stunned and delighted (beyond all measure) by the elegance and clarity of this result. I knew from my previous analysis what the general pattern would show, but I never dreamed that the decline of variation would be so regular, so devoid of exception or anomaly for even a single year, so unvarying that we could even pick out such subtleties as a deceleration in decline. I have spent my entire professional career studying such statistical distributions, and I know how rarely one obtains such clean results in better-behaved data of controlled experiments or natural growth in simple systems. We usually encounter some glitch, some anomaly, some funny years. But the decline of standard deviations for batting averages is so regular that the pattern of Figure 16 looks like a plot for a law of nature.
I find the regularity all the more remarkable because the graph of mean batting averages themselves through time (Figure 14) shows all the noise and fluctuation expected in natural systems. These mean batting averages have frequently been manipulated by the rulemakers of baseball to maintain a general constancy, while no one has tried to monkey with the standard deviations. Nonetheless, while mean batting averages go up and down to follow the whims of history and the vagaries of invention, the standard deviation has marched steadily down at a decreasing pace, apparently disturbed by nothing of note, apparently following some interesting rule or general principle in the behavior of systems—a principle that should provide a solution to the classic dilemma of why 0.400 hitting has disappeared.
The details of Figure 16 are impressive in their exceptionless regularity. All four beginning years of the 1870s feature high values of standard deviations greater than 0.050, while the last reading in excess of 0.050 occurs in 1886. Values between 0.04 and 0.05 characterize the remainder of the nineteenth century, with three years just below at 0.038 to 0.040. But the last reading in excess of 0.040 occurs in 1911. Subsequently, decline within the 0.03-to-0.04 range shows the same precision of detail in unreversed decrease over many years. The last reading as high as 0.037 occurs in 1937, and of 0.035 in 1941. Only two years have exceeded 0.034 since 1957. Between 1942 and 1980, values remained entirely within the restricted range of 0.0285 to 0.0343. I had thought that at least one unusual year would upset the pattern, that at least one nineteenth-century value would reach a late-twentieth-century low, or one recent year soar to a nineteenth-century high—but nothing of the sort occurs. All yearly measures from 1906 back to the beginning of major league baseball are higher than every reading from 1938 to 1980. We find no overlap at all. Speaking as an old statistical trouper, I can assure you that this pattern represents regularity with a vengeance. This analysis has uncovered something general, something beyond the peculiarity of an idiosyncratic system, some rule or principle that should help us to understand why 0.400 hitting has become extinct in baseball.
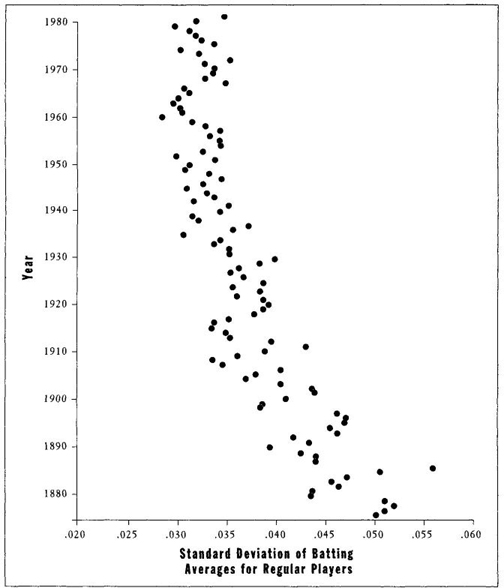
FIGURE 16 Standard deviation of batting averages for all full-time players by year for the first 100 years of professional baseball. Note the regular decline.
10
Why the Death of 0.400 Hitting Records Improvement of Play
So far I have only demonstrated a pattern based on unconventional concepts and pictures. I have not yet proposed an explanation. I have proposed that 0.400 hitting be reconceptualized as an inextricable segment in a full house of variation—as the right tail of the bell curve of batting averages— and not as a self-contained entity whose disappearance must record the degeneration of batting in some form or other.
In this different model and picture, 0.400 hitting disappears as a consequence of shrinking variation around a stable mean batting average. The shrinkage is so exceptionless, so apparently lawlike in its regularity, that we must be discerning something general about the behavior of systems through time.
Why should such a shrinkage of variation record the worsening of anything? The final and explanatory step in my argument must proceed beyond the statistical analysis of batting averages. We must consider both the nature of baseball as a system, and some general properties of systems that enjoy long persistence with no major changes in procedures and behaviors. I therefore devote this section to reasons for celebrating the loss of 0.400 hitting as a mark of better baseball.
Two arguments, and supporting data, convince me that shrinkage of variation (with consequent disappearance of 0.400 hitting) must be measuring a general improvement of play. The two formulations sound quite dissimilar at first, but really represent different facets of a single argument.
1. Complex systems improve when the best performers play by the same rules over extended periods of time. As systems improve, they equilibrate and variation decreases. No other major American sport permits such an analysis, for all others have changed their fundamental rules too often and too recently. As a teenager, I played basketball without the twenty-four-second rule. My father played with a center jump after each basket. His father (had he been either inclined or acculturated) would have brought the ball down-court with a two-handed dribble. And Mr. Naismith’s boys threw the ball into a peach basket. While the peach basket still hung in the 1890s, baseball made its last major change in procedure (as discussed in the last chapter) by moving the pitcher’s mound back to the current distance of sixty feet six inches.
But constant rules don’t imply unchanging practices. (In the last chapter I discussed the numerous fiddlings and jigglings imposed by rulemakers to keep pitching and hitting in balance.) Dedicated performers are constantly watching, thinking, and struggling for ways to twiddle or manipulate the system in order to gain a legitimate edge (new techniques for hitting a curve, for gobbling up a ground ball, for gyrating in a windup to fool the batter). Word spreads, and these minor discoveries begin to pervade the system. The net result through time must inevitably encourage an ever-closer approach to optimal performance in all aspects of play— combined with ever-decreasing variation in modes of procedure.
Baseball was feeling its juvenile way during the early days of major league play. The basic rules of the 1890s are still our rules, but scores of subtleties hadn’t yet been invented or developed. Rough edges careered out in all directions from a stable center. To cite just a few examples (taken from Bill James’s Historical Baseball Abstract): pitchers only began to cover first base in the 1890s. During the same decade, Brooklyn developed the cutoff play, while the Boston Beaneaters invented the hit-and-run, and signals from runner to batter. Gloves were a joke in these early days—just a bit of leather over the hand, not today’s baskets for trapping balls. As a fine symbol of broader tolerance and variation, the 1896 Philadelphia Phillies actually experimented for seventy-three games with a lefty shortstop. Unsurprisingly, traditional wisdom applied. He stank—turning in the worst fielding average with the fewest assists among all regular shortstops in the league.
In baseball’s youth, styles of play had not become sufficiently regular and optimized to foil the accomplishments of the very best. Wee Willie Keeler could "hit ’em where they ain’t" (his motto), and compile a 0.432 batting average in 1897, because fielders didn’t yet know where they should be. Slowly, by long distillation of experience, players moved toward optimal methods of positioning, fielding, pitching, and batting
—
and variation inevitably declined. The best now meet an opposition too finely honed to its own perfection to permit the extremes of accomplishment that characterized a more casual and experimental age. We cannot explain the disappearance of 0.400 hitting simply by saying (however true) that managers invented relief pitching, while pitchers invented the slider—for such traditional explanations abstract 0.400 hitting as an independent phenomenon and view its extinction as the chief sign of a trend to deterioration in batting. Rather, hitting has improved along with all other aspects of play as the entire game sharpened its standards, narrowed its ranges of tolerance, and therefore limited variation in performance as all parts of the game climbed a broader-based hill toward a much narrower pinnacle.
Consider the predicament of a modern Wade Boggs, Tony Gwynn, Rod Carew, or George Brett. Can anyone truly believe that these great hitters are worse than Wee Willie Keeler (at five feet four and a half inches and 140 pounds), Ty Cobb, or Rogers Hornsby? Every pitch is now charted, every hit mapped to the nearest square inch. Fielding and relaying have improved dramatically. Fresh and rested pitching arms must be faced in the late innings; fielders scoop up grounders in gloves as big as a brontosaurus’s footprint. Relative to the right wall of human limitation, Tony Gwynn and Wee Willie Keeler must stand in the same place—just a few inches from theoretical perfection (the best that human muscles and bones can do). But average play has so crept up upon Gwynn that he lacks the space for taking advantage of suboptimality in others. All these general improvements must rob great batters of ten to twenty hits a year—a bonus that would be more than enough to convert any of the great modern batters into 0.400 hitters.
I have formulated the argument parochially in the terms and personnel of baseball. But I feel confident that I am describing a general property of systems composed of individual units competing with one another under stable rules and for prizes of victory. Individual players struggle to find means for improvement—up to limits imposed by balances of competition and mechanical properties of materials—and their discoveries accumulate within the system, leading to general gains toward an optimum. As the system nears this narrow pinnacle, variation must decrease— for only the very best can now enter, while their predecessors have slowly, by trial and error, discovered better procedures that now cannot be substantially improved. When someone discovers a truly superior way, everyone else copies and variation diminishes.
Thus I suspect that similar reasons (along with a good dollop of historical happenstance) govern the uniformity of automotive settling upon internal combustion engines from a wider set of initial possibilities in
-
cluding steam and electric power; the standardization of business practices; the reduction of life’s initial multicellular animal diversity to just a handful of major phyla (see Gould, 1989); and the disappearance of 0.400 hitting in baseball as variation shrinks symmetrically around a stable mean batting average.
In the good old days of greater variation and poorer play, you could get a job for "good field, no hit"—but no longer as the game improved and the pool of applicants widened. So the left tail shriveled up and moved toward the mean. In those same legendary days, the very best hitters could take advantage of a sloppier system that had not yet discovered optimalities of opposing activities in fielding and pitching. Our modern best hitters are just as good and probably better, but average pitching and fielding have so improved that the truly superb cannot soar so far above the ordinary. Therefore the right tail shriveled up and also moved toward the mean.

FIGURE 17 Increasing specialization as shown by decline in the number of players who fielded more than one position in a given year.
I first published these ideas in the initial issue of the revived Vanity Fair in March 1983. To my gratification, several fellow sabermetricians became intrigued and took up the challenge to test my ideas with other sources of baseball data. The results have been most gratifying. In particular, my colleagues have provided good examples of the two most important predictions made by models for general improvement marked by decreasing variation.
Specialization and division of labor. Ever since Adam Smith began The Wealth of Nations with his famous example of pinmaking, specialization and division of labor have been viewed as the major criteria of increasing efficiency and approach to optimality. In their paper "On the tendency toward increasing specialization following the inception of a complex system—professional baseball 1871-1988," John Fellows, Pete Palmer, and Steve Mann plotted the number of major leaguers who played more than one fielding position in a single season. Note (see Figure 17) the steady decrease and subsequent stabilization, a pattern much like the decelerating decline of standard deviations in Figure 16—though in this case measuring the increase of specialization through baseball’s history (I do not know why values rose slightly in the 1960s, though to nowhere near the high levels of baseball’s early history).
Decreasing variation. My colleagues Sangit Chatterjee and Mustafa Yilmaz of the College of Business Administration at Northeastern University (baseball does provide some wonderful cohesion amid our diversity) wrote an article on "Parity in baseball: stability of evolving systems." In searching for an example even more general than shrinking variation in batting averages, Chatterjee and Yilmaz reasoned that if general play has improved, with less variation among a group of consistently better players, then disparity among teams should also decrease—that is, the difference between the best and worst clubs should decline because all teams can now fill their rosters with enough good players, leading to greater equalization through time. The authors therefore plotted the stan
-
dard deviation in seasonal winning percentage from the beginning of major league baseball to the present. Figure 18 shows a steady fall in standard deviation, indicating a decreasing difference between the best and worst teams through the history of play.
7
2. As play improves and bell curves march toward the right wall, variation must shrink at the right tail. I discussed the notion of "walls" in chapter 4— upper and lower limits to variation imposed by laws of nature, structure of materials, etc. (There I illustrated a minimal left wall in the story of my medical history—an obvious and logical lower bound of zero time between diagnosis and death from the same disease. Part Four will focus upon a left wall of minimal complexity for life—for nothing much simpler than a bacterial cell could be preserved in the fossil record.) We would all, I think, accept the notion that a "right wall" must exist for human achievement. We cannot, after all, perform beyond the limits of what human bone and muscle can accomplish; no man will ever outpace a cheetah or a finch. We would also, I assume, acknowledge that some extraordinary people, by combination of genetic gift, maniacal dedication, and rigorous training, push their bodies to perform as close to the right wall as human achievement will allow.
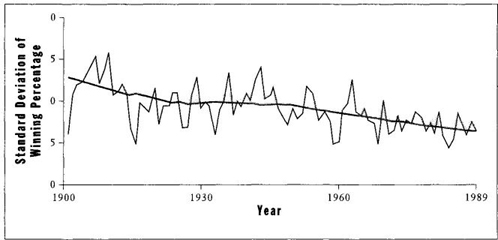
FIGURE 18 Decline in the standard deviation of winning percentage for all teams in the National League through time. The trend shows greater equalization of teams in the history of baseball, a consequence of increasing general excellence of play.
Earlier I discussed the major phenomenon in sports that must be signaling approach to the right wall—a flattening out of improvement (measured by record breaking) as sports mature, promise ever greater rewards, become accessible to all, and optimize methods of training (see pp. 92—97). This flattening out must represent the approach of the best to the right wall. The longer a sport has endured with stable rules and maximal access, the closer the best should stand to the right wall, and the less we should therefore expect any sudden and massive breaking of records. When George Plimpton, several years ago, wrote about a great pitching prospect who could throw 140 miles per hour, all serious fans recognized this essay in "straight" reporting as a spoof, though many less knowledgeable folks were fooled. From Walter Johnson in the 1920s to Nolan Ryan today, the best fastball pitchers have tried to throw at maximal speed, and no one has consistently broken 100 mph. In fact, Johnson was probably as fast as Ryan. Thus, we can assume that these men stand near the right wall of what a human arm can do. Barring some unexpected invention in technique, no one is going to descend from some baseball Valhalla and start throwing 40 percent again as fast—not after a century of trying among the very best.
