Full House (13 page)

These approaches to the right wall can easily be discerned in sports that keep absolute records measured as times and distances. As previously discussed, record times for the marathon, or virtually any other timed event with stable rules and no major innovations, drop steadily—in the decelerating pattern of initial rapidity, followed by later plateauing as the best draw near to the right wall. But this pattern is masked in baseball, because most records measure one activity relative to another, and not against an absolute standard of time or distance. Batting records mark what a hitter does against pitchers. A mean league batting average of 0.260 is not an absolute measure of anything, but a general rate of success for hitters versus pitchers. Therefore a fall or rise in mean batting average does not imply that hitters are becoming absolutely worse or better, but only that their performance relative to pitchers has changed.
Thus we have been fooled in reading baseball records. We note that the mean batting average has never strayed much from 0.260, and we therefore wrongly assume that batting skills have remained in a century-long rut. We note that 0.400 hitting has disappeared, and we falsely assume that great hitting has gone belly-up. But when we recognize these averages as relative records, and acknowledge that baseball professionals, like all other premier athletes, must be improving with time, a different (and almost surely correct) picture emerges (see Figure 19)—one that acknowledges batting averages as components in a full house of variation with a bell-curve distribution and that, as an incidental consequence of no mean importance, allows us finally to visualize why the extinction of 0.400 hitting must be measuring improvement of play as marked by shrinking variation.
Early in the history of baseball (top part of Figure 19), average play stood far from the right wall of human limits. Both hitters and pitchers performed considerably below modern standards, but the balance between them did not differ from today’s—and we measure this unchanging balance as 0.260 hitting. Thus, in these early days, the mean batting average of 0.260 fell well below the right wall, and variation spread out widely on both sides—at the lower end, because the looser and less accomplished system did provide jobs to good fielders who couldn’t hit; and at the upper end, because so much space existed between the average and the right wall.
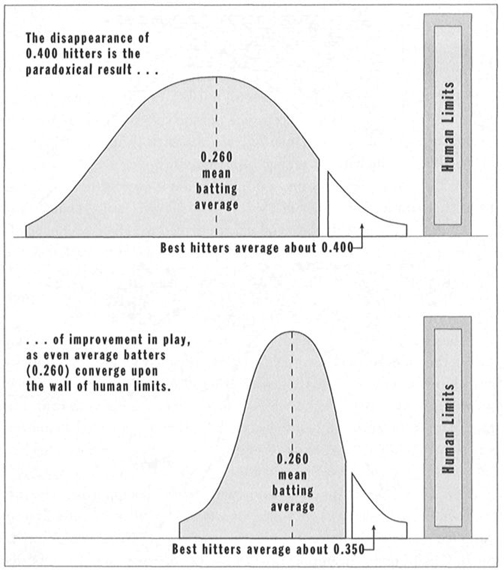
FIGURE 19 Four hundred hitting disappears as play improves and the entire bell curve moves closer to the right wall of human limits while variation declines. Upper chart: early twentieth-century baseball. Lower chart: current baseball.
A few men of extraordinary talent and dedication always push their skills to the very limit of human accomplishment and reside near the right wall. In baseball’s early days, these men stood so far above the mean that we measured their superior performance as 0.400 batting.
Consider what has happened to modern baseball (lower part of Figure 19). General play has improved significantly in all aspects of the game. But the balance between hitting and pitching has not altered. (I showed on pp. 101-105 that the standardbearers of baseball have frequently fiddled with the rules in order to maintain this balance.) The mean batting average has therefore remained constant, but this stable number represents markedly superior performance today (in both hitting and pitching). Therefore, this unchanged average must now reside much closer to the right wall. Meanwhile, and inevitably, variation in the entire system has shriveled symmetrically on both sides—at the lower end, because improvement of play now debars employment to men who field well but cannot hit; and at the upper end, for the simple reason that much less room now exists between the upwardly mobile mean and the unchanging right wall. The top hitters, trapped at the upper bound of the right wall, must now lie closer to the mean than did their counterparts of yore.
The best hitters of today can’t be worse than 0.400 hitters of the past. In fact, the modern stars may have improved slightly and may now stand an inch or two closer to the right wall. But the average player has moved several feet closer to the right wall—and the distance between ordinary (maintained at 0.260) and best has decreased, thereby erasing batting averages as high as 0.400. Ironically, therefore, the disappearance of 0.400 hitting marks the general improvement of play, not a decline in anything.
Our confidence in this explanation will increase if supporting data can be provided with statistics for other aspects of play through time. I have compiled similar records for the other two major facets of baseball—field— ing and pitching. Both support the key predictions of a model that posits increasing excellence of play with decreasing variation when the best can no longer take such numerical advantage of the poorer quality in average performance.
Most batting and pitching records are relative, but the primary measure of good fielding is absolute (or at least effectively so). A fielding average is you against the ball, and I don’t think that grounders or fly balls have improved through time (though the hitters have). I suspect that modern fielders are trying to accomplish the same tasks, at about the same level of difficulty, as their older counterparts. Fielding averages (the percent of errorless chances) should therefore provide an absolute measure of changing excellence in play. If baseball has improved, we should note a decelerating rise in fielding averages through time. (I do recognize that some improvement might be attributed to changing conditions, rather than absolutely improving play, just as some running records may fall because modern tracks are better raked and pitched. Older infields were, apparently, lumpier and bumpier than the productions of good ground crews today—so some of the poorer fielding of early days may have resulted from lousy fields rather than lousy fielders. I also recognize that rising averages must be tied in large part to great improvement in the design of gloves— but better equipment represents a major theme of history, and one of the legitimate reasons underlying my claim for general improvement in play.)
Following the procedure of my first compilation on batting averages, I computed both the league fielding average for all regular players and the mean score of the five best for each year since the beginning of major league play in 1876. Figure 20, showing decadal averages for the National League through time, confirms the predictions in a striking manner. Not only does improvement decelerate strongly with time, but the decrease is continuous and entirely unreversed, even for the tiny increments of the last few decades, as averages reach a plateau so near the right wall.
For the first half of baseball (the fifty-five years from 1876 to 1930), decadal fielding averages rose from 0.9622 to 0.9925 for the best players, for a total gain of 0.0303; and from 0.8872 to 0.9685 for average performers, for a total gain of 0.0813. (For a good sense of total improvement, note that the average player of the 1920s did a tiny bit better than the very best fielders of the 1870s.) For baseball’s second half (the fifty years from 1931 to 1980), the increase slowed substantially, but never stopped. Decadal averages for the best players rose from 0.9940 to 0.9968, for a small total gain of 0.0028—or less than 10 percent of the recorded rise of baseball’s first half. Over the same fifty years, values for league averages rose from 0.971 for the 1930s to 0.9774 for the 1970s, a total gain of 0.0064—again less than 10 percent of the improvement recorded during the same number of years during baseball’s first half.
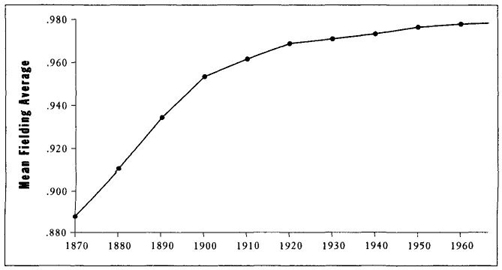
FIGURE 20 Unreversed, but constantly slowing, improvement in mean fielding average through the history of baseball.
These data continue to excite me. As stated before, I have spent a professional lifetime compiling statistical data of this sort for the growth of organisms and the evolution of lineages. I have a sense of the patterns expected from such data, and have learned to pay special attention to noise and inevitable departures from expectations. I am just not used to the exceptionless data produced over and over again by the history of baseball. I would have thought that any human institution must be more sensitive than natural systems to the vagaries of accident and history, and that baseball would therefore yield more exceptions and a fuzzier signal (if any at all). And yet, here again—as with the decline of standard deviations in batting averages (see page 106)—I find absolute regularity of change, even when the total accumulation is so small that one would expect some exceptions just from the inevitable statistical errors of life and computation. Again, I get the eerie feeling that I must be calculating something quite general about the nature of systems, and not just compiling the individualized numbers of a particular and idiosyncratic institution (yes, I know, it’s just a feeling, not a proof). Baseball is a truly remarkable system for statisticians, manifesting two properties devoutly to be wished, but not often encountered, in actual data: an institution that has worked by the same rules for a century, and has compiled complete data (nothing major missing) on all measurable aspects of its history.
For example, as decadal averages for the five best reach their plateau in baseball’s second half, improvement slows markedly, but never reverses—the total rise of only 0.0028 occurs in a steady climb by tiny increments: 0.9940, 0.9953, 0.9958, and 0.9968. Lest one consider these gains too small to be anything but accidental, the first achievements of individual yearly values also show the same pattern. Who would have thought that the rise from 0.990 to 0.991 to 0.992, and so on, could mean anything at all? An increment of one in the third decimal place can’t possibly be measuring anything significant about actual play. And yet 0.990 is first reached in 1907, 0.991 in 1909, 0.992 in 1914, 0.993 in 1915, 0.994 in 1922, 0.995 in 1930. Then, thank goodness, I find one tiny break in pattern (for I was beginning to think that baseball’s God had decided to mock me; the natural world is supposed to contain exceptions). The first value of 0.996 occurs in 1948, but the sharp fielders of 1946 got to 0.997 first! Then we are back on track and do not reach 0.998 until 1972.
This remarkable regularity can occur only because, as my hypothesis requires in its major contention, variation declines so powerfully through time and becomes so restricted in later years. (With such limited variation from year to year, any general signal, however weak, should be more easily detected.) For example, yearly values during the 1930s range only from 0.992 to 0.995 for best scores, and from 0.968 to 0.973 for average scores. By contrast, during baseball’s first full decade of the 1880s, the yearly best ranged from 0.966 to 0.981, and the average from 0.891 to 0.927.
This regularity may be affirmed with parallel data for the American League (shown with the National League in Table 3). Again, we find unreversed decline, though this time with one exception as American League values fall slightly during the 1970s—and I have no idea why (if one can properly even ask such a question for such a minuscule effect). Note the remarkable similarity between the leagues in rates of improvement across decades. We are not, of course, observing two independent systems, for styles of play do alter roughly in parallel as both leagues form a single institution (with some minor exceptions, as the National League’s blessed refusal to adopt the designated hitter rule indicates in our times). But nearly identical behavior in two cases does show that we are probably picking up a true signal and not a statistical accident.
Data on fielding averages are particularly well suited to illustrate the focal concept of right walls—the key notion behind my second explanation for viewing the disappearance of 0.400 hitting as a sign of general improvement in play. Fielding averages have an absolute, natural, and logical right wall of 1.000—for 1.000 represents errorless play, and you cannot make a negative number of errors! Today’s best fielders are standing with toes already grazing the right wall—0.998 is about an error per year, and nobody can be absolutely perfect. (Outfielders, pitchers, and catchers occasionally turn in seasons of 1.000 fielding, but only one infielder has ever done so for a full season’s regular play—Steve Garvey at first base in 1984.)
